この記事ではRLC直列回路の『合成インピーダンス』について
- RLC直列回路の『合成インピーダンス』の式・大きさ・ベクトル図・インピーダンス角
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
RLC直列回路の『合成インピーダンス』
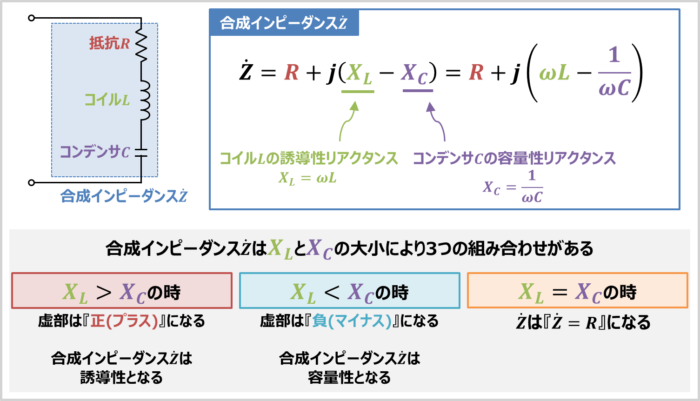
RLC直列回路は上図に示すように、抵抗\(R\)とコイル\(L\)とコンデンサ\(C\)を直列に接続した回路です。
抵抗\(R\)の抵抗値を\(R{\mathrm{[{\Omega}]}}\)、コイル\(L\)の自己インダクタンスを\(L{\mathrm{[H]}}\)、コンデンサ\(C\)の静電容量を\(C{\mathrm{[F]}}\)とします。この時、抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)、コイル\(L\)のインピーダンス\({\dot{Z}}_L\)、コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)はそれぞれ次式で表されます。
\begin{eqnarray}
{\dot{Z}}_R&=&R\tag{1}\\
\\
{\dot{Z}}_L&=&jX_L=j{\omega}L\tag{2}\\
\\
{\dot{Z}}_C&=&-jX_C=-j\frac{1}{{\omega}C}=\frac{1}{j{\omega}C}\tag{3}
\end{eqnarray}
(2)式と(3)式において、\(X_L\left(={\omega}L\right)\)は誘導性リアクタンス(コイル\(L\)の抵抗成分)、\(X_C\left(=\displaystyle\frac{1}{{\omega}C}\right)\)は容量性リアクタンス(コンデンサ\(C\)の抵抗成分)と呼ばれています。また、\({\omega}\)は角周波数(角速度とも呼ばれる)であり、\({\omega}=2{\pi}f\)の関係があります。
なお、リアクタンスについては下記の記事で詳しく説明していますので、参考になると幸いです。
あわせて読みたい
『リアクタンス』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る
【リアクタンスとは】『単位』や『計算方法』などのまとめ!
RLC直列回路の合成インピーダンス\({\dot{Z}}\)はそれぞれのインピーダンスを足したものなので次式となります。
RLC直列回路の合成インピーダンス
\begin{eqnarray}
{\dot{Z}}&=&{\dot{Z}}_R+{\dot{Z}}_L+{\dot{Z}}_C\\
\\
&=&R+jX_L-jX_C\\
\\
&=&R+j\left(X_L-X_C\right)\\
\\
&=&R+j\left({\omega}L-\frac{1}{{\omega}C}\right){\mathrm{[{\Omega}]}}\tag{4}
\end{eqnarray}
RLC直列回路の合成インピーダンス\({\dot{Z}}\)は『誘導性リアクタンス\(X_L={\omega}L\)』と『容量性リアクタンス\(X_C=\displaystyle\frac{1}{{\omega}C}\)』の大小により、以下の3つの組み合わせができます。
- \(X_L{\;}{\gt}{\;}X_C\)の時
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも大きい場合、『虚部\(X_L-X_C\)』が『正(プラス)』になるため、合成インピーダンス\({\dot{Z}}\)は誘導性となります。
- \(X_L{\;}{\lt}{\;}X_C\)の時
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも小さい場合、『虚部\(X_L-X_C\)』が『負(マイナス)』になるため、合成インピーダンス\({\dot{Z}}\)は容量性となります。
- \(X_L=X_C\)の時
- 『誘導性リアクタンス\(X_L\)』と『容量性リアクタンス\(X_C\)』が等しい場合、合成インピーダンスは『\({\dot{Z}}=R\)』になります。\(X_L\)と\(X_C\)が等しくなっている時、回路は直列共振をしている状態です。直列共振が成り立つ時の角周波数\({\omega}\)及び周波数\(f\)は下記となります。
\begin{eqnarray}
X_L&=&X_C\\
\\
{\omega}L&=&\frac{1}{{\omega}C}\\
\\
{\Leftrightarrow}{\omega}&=&\frac{1}{\sqrt{LC}}\\
\\
{\Leftrightarrow}f&=&\frac{1}{2{\pi}\sqrt{LC}}\tag{5}
\end{eqnarray}
- 『誘導性リアクタンス\(X_L\)』と『容量性リアクタンス\(X_C\)』が等しい場合、合成インピーダンスは『\({\dot{Z}}=R\)』になります。\(X_L\)と\(X_C\)が等しくなっている時、回路は直列共振をしている状態です。直列共振が成り立つ時の角周波数\({\omega}\)及び周波数\(f\)は下記となります。
RLC直列回路の『合成インピーダンス』の大きさ
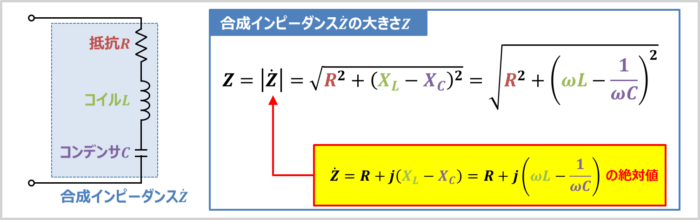

先ほど次式で表される合成インピーダンス\({\dot{Z}}\)を求めました。
\begin{eqnarray}
{\dot{Z}}=R+j\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right){\mathrm{[{\Omega}]}}\tag{6}
\end{eqnarray}
RLC直列回路の合成インピーダンスの大きさ\(Z\)は(6)式の合成インピーダンス\({\dot{Z}}\)の絶対値となります。
もう少し詳しく説明すると、合成インピーダンスの大きさ\(Z\)は『\({\dot{Z}}=R+j\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)\)』において、『実部\(R\)の2乗』と『虚部\({\omega}L-\displaystyle\frac{1}{{\omega}C}\)の2乗』を足して、平方根を取ることで求めることができ、式で表すと次式となります。
RLC直列回路の合成インピーダンスの大きさ
\begin{eqnarray}
Z=|{\dot{Z}}|=\sqrt{R^2+\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)^2}{\mathrm{[{\Omega}]}}\tag{7}
\end{eqnarray}
なお、抵抗\(R\)のインピーダンスの大きさ\(Z_R\)、コイル\(L\)のインピーダンスの大きさ\(Z_L\)、コンデンサ\(C\)のインピーダンスの大きさ\(Z_C\)は次式で表されます。
\begin{eqnarray}
Z_R&=&|{\dot{Z}}_R|=\sqrt{R^2}=R\tag{8}\\
\\
Z_L&=&|{\dot{Z}}_L|=\sqrt{({\omega}L)^2}={\omega}L\tag{9}\\
\\
Z_C&=&|{\dot{Z}}_C|=\sqrt{\left(\displaystyle\frac{1}{{\omega}C}\right)^2}=\displaystyle\frac{1}{{\omega}C}\tag{10}
\end{eqnarray}
インピーダンスに付いている「ドット」の意味
インピーダンス(Z)の記号の上に「・(ドット)」が付き、\({\dot{Z}}\)となっているものがあります。
このドットがついた\({\dot{Z}}\)は「ベクトルですよ!」ということを表しています。
ドットが付く場合(\({\dot{Z}}\)など)はベクトル(複素数)を表し、ドットが付かない場合(\(Z\)など)はベクトルの絶対値(大きさ、長さ)を表しています。
詳しくは下記の記事で説明していますので、ご参考になれば幸いです。 続きを見る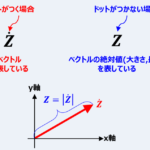


【交流回路とベクトル】インピーダンスなどにつく「・(ドット)」の意味!
RLC直列回路の『合成インピーダンス』のベクトル図
RLC直列回路の合成インピーダンス\({\dot{Z}}\)の『ベクトル図』は下記のステップで描くことができます。
『ベクトル図』の描き方
- 抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)のベクトルを描く
- コイル\(L\)のインピーダンス\({\dot{Z}}_L\)のベクトルを描く
- コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)のベクトルを描く
- 各ベクトルを合成する
では各ステップについて順番に説明していきます。
抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)のベクトルを描く


抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)は次式で表されます。
\begin{eqnarray}
{\dot{Z}}_R=R\tag{11}
\end{eqnarray}
そのため、抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)のベクトルの向きは実数軸の向きとなります。式に虚数単位\(j\)が付かない場合はベクトルは回転せず、実軸の向きとなります。ベクトルの向きの決め方については後ほど詳しく説明します。
また、抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)のベクトルの大きさ(長さ)\(Z_R\)は次式となります。
\begin{eqnarray}
Z_R=|{\dot{Z}}_R|=R\tag{12}
\end{eqnarray}
コイル\(L\)のインピーダンス\({\dot{Z}}_L\)のベクトルを描く
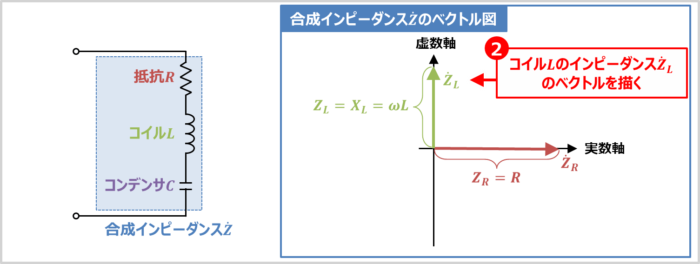

コイル\(L\)のインピーダンス\({\dot{Z}}_L\)は次式で表されます。
\begin{eqnarray}
{\dot{Z}}_L=j{\omega}L\tag{13}
\end{eqnarray}
そのため、コイル\(L\)のインピーダンス\({\dot{Z}}_L\)のベクトルの向きは実数軸を反時計周りに90°回転した向きになります(式に『\(+j\)』が付くとベクトルが反時計周りに90°回転します)。ベクトルの向きの決め方については後ほど詳しく説明します。
また、コイル\(L\)のインピーダンス\({\dot{Z}}_L\)のベクトルの大きさ(長さ)\(Z_L\)は次式となります。
\begin{eqnarray}
Z_L=|{\dot{Z}}_L|={\omega}L\tag{14}
\end{eqnarray}
コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)のベクトルを描く
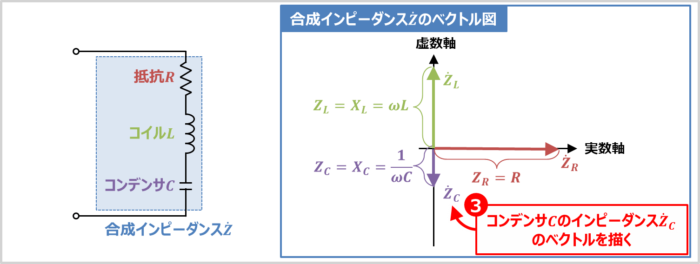

コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)は次式で表されます。
\begin{eqnarray}
{\dot{Z}}_C=-j\displaystyle\frac{1}{{\omega}C}\tag{15}
\end{eqnarray}
そのため、コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)のベクトルの向きは実数軸を時計周りに90°回転した向きになります(式に『\(-j\)』が付くとベクトルが時計周りに90°回転します)。ベクトルの向きの決め方については後ほど詳しく説明します。
また、コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)のベクトルの大きさ(長さ)\(Z_C\)は次式となります。
\begin{eqnarray}
Z_C=|{\dot{Z}}_C|=\displaystyle\frac{1}{{\omega}C}\tag{16}
\end{eqnarray}
各ベクトルを合成する
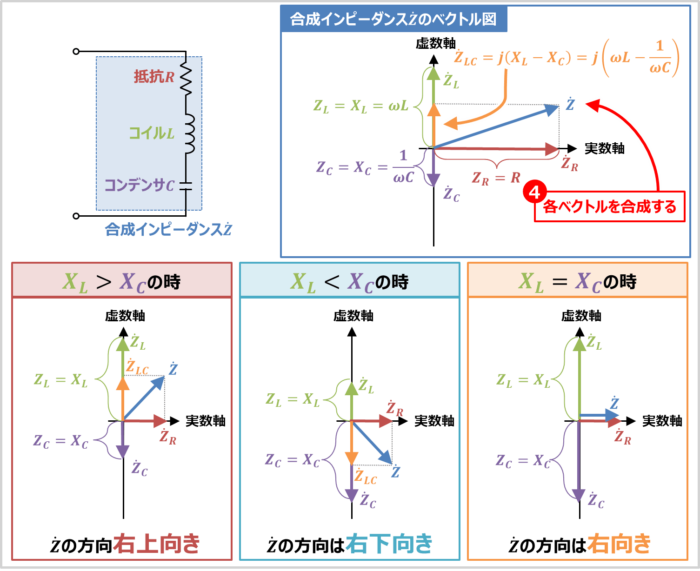

『抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)』と『コイル\(L\)のインピーダンス\({\dot{Z}}_L\)』と『コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)』のベクトルの合成が RLC直列回路の合成インピーダンス\({\dot{Z}}\)のベクトル図となります。
繰り返しになりますが、RLC直列回路の合成インピーダンス\({\dot{Z}}\)は次式で表されます。
\begin{eqnarray}
{\dot{Z}}&=&{\dot{Z}}_R+{\dot{Z}}_L+{\dot{Z}}_C\\
\\
&=&R+jX_L-jX_C\\
\\
&=&R+j\left(X_L-X_C\right)\\
\\
&=&R+j\left({\omega}L-\frac{1}{{\omega}C}\right)\tag{17}
\end{eqnarray}
上式の括弧の中にある『誘導性リアクタンス\(X_L={\omega}L\)』と『容量性リアクタンス\(X_C=\displaystyle\frac{1}{{\omega}C}\)』の大小により、合成インピーダンス\({\dot{Z}}\)のベクトル方向が変わるので注意が必要です。
- \(X_L{\;}{\gt}{\;}X_C\)の時
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも大きい場合、合成インピーダンス\({\dot{Z}}\)のベクトルの方向は右上向きになります。
- \(X_L{\;}{\lt}{\;}X_C\)の時
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも小さい場合、合成インピーダンス\({\dot{Z}}\)のベクトルの方向は右下向きになります。
- \(X_L=X_C\)の時
- 『誘導性リアクタンス\(X_L\)』と『容量性リアクタンス\(X_C\)』が等しい場合、合成インピーダンス\({\dot{Z}}\)は『\({\dot{Z}}=R\)』になるため、ベクトルの方向は右向きになります。
RLC直列回路の合成インピーダンス\({\dot{Z}}\)のベクトルの大きさ(長さ)\(Z\)は次式で表されます。
\begin{eqnarray}
Z=|{\dot{Z}}|=\sqrt{R^2+\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)^2}\tag{18}
\end{eqnarray}
RLC直列回路の合成インピーダンス\({\dot{Z}}\)のベクトルの大きさ(長さ)\(Z=\sqrt{R^2+\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)^2}\)はベクトル図において三平方の定理(ピタゴラスの定理)を用いても求めることができます。
ベクトルの向きについて
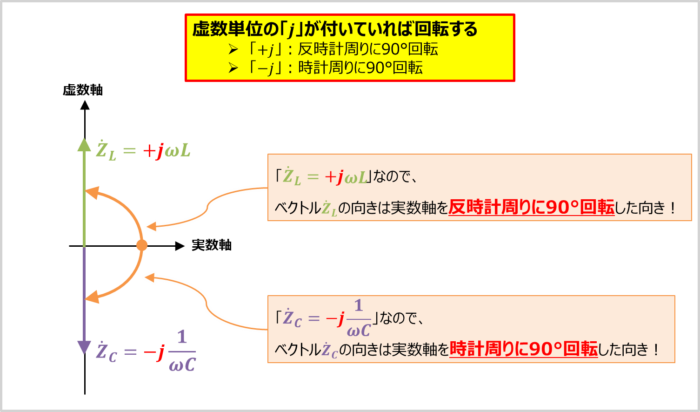

ベクトルの向きの決め方についてもう少し詳しく説明します。
ベクトルの『向き』について
式に虚数単位『\(j\)』が付くとベクトルの向きが90°回転します。
- 『\(+j\)』が付いている時
- ベクトルは反時計周りに90°回転します。
- 『\(-j\)』が付いている時
- ベクトルは時計周りに90°回転します。
コイル\(L\)のインピーダンス\({\dot{Z}}_L\)は次式で表されます。
\begin{eqnarray}
{\dot{Z}}_L=j{\omega}L\tag{19}
\end{eqnarray}
コイル\(L\)のインピーダンス\({\dot{Z}}_L\)の式には『\(+j\)』が付いているので、ベクトル\({\dot{Z}}_L\)の向きは実数軸を反時計周りに90°回転した向きとなります。
一方、コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)は次式で表されます。
\begin{eqnarray}
{\dot{Z}}_C=-j\displaystyle\frac{1}{{\omega}C}\tag{20}
\end{eqnarray}
コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)の式には『\(-j\)』が付いているので、ベクトル\({\dot{Z}}_C\)の向きは実数軸を時計周りに90°回転した向きとなります。
RLC直列回路の『合成インピーダンス』のインピーダンス角


『誘導性リアクタンス\(X_L={\omega}L\)』と『容量性リアクタンス\(X_C=\displaystyle\frac{1}{{\omega}C}\)』の大小により、インピーダンス角\({\theta}\)が異なります。
- \(X_L{\;}{\gt}{\;}X_C\)の時
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも大きい場合、インピーダンス角\({\theta}\)は以下の値となります。
\begin{eqnarray}
{\theta}&=&{\tan}^{-1}\left(\frac{X_L-X_C}{R}\right){\mathrm{[rad]}}\tag{21}
\end{eqnarray}
インピーダンス角\({\theta}\)はプラスとなります。
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも大きい場合、インピーダンス角\({\theta}\)は以下の値となります。
- \(X_L{\;}{\lt}{\;}X_C\)の時
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも小さい場合、インピーダンス角\({\theta}\)は以下の値となります。
\begin{eqnarray}
{\theta}&=&{\tan}^{-1}\left(\frac{X_L-X_C}{R}\right){\mathrm{[rad]}}\tag{22}
\end{eqnarray}
インピーダンス角\({\theta}\)はマイナスとなります。
- 『誘導性リアクタンス\(X_L\)』が『容量性リアクタンス\(X_C\)』よりも小さい場合、インピーダンス角\({\theta}\)は以下の値となります。
- \(X_L=X_C\)の時
- 『誘導性リアクタンス\(X_L\)』と『容量性リアクタンス\(X_C\)』が等しい場合、インピーダンス角\({\theta}\)は以下の値となります。
\begin{eqnarray}
{\theta}=0{\mathrm{[rad]}}\tag{23}
\end{eqnarray}
- 『誘導性リアクタンス\(X_L\)』と『容量性リアクタンス\(X_C\)』が等しい場合、インピーダンス角\({\theta}\)は以下の値となります。
まとめ
この記事ではRLC直列回路の『合成インピーダンス』について、以下の内容を説明しました。
- RLC直列回路の『合成インピーダンス』の式・大きさ・ベクトル図・インピーダンス角
お読み頂きありがとうございました。
あわせて読みたい
直列回路と並列回路の『合成インピーダンス』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






