抵抗の温度特性について！抵抗温度係数ってなに？

この記事では『抵抗』について

抵抗の温度特性
抵抗の温度特性を決める『抵抗温度係数』

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

抵抗の温度特性

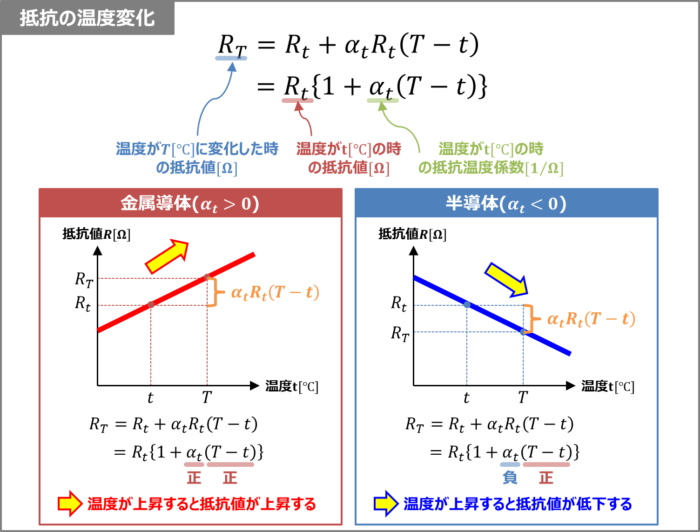
一般的に、金属導体の抵抗値は温度が上昇すると増加し、半導体の抵抗値は温度が上昇すると減少します。

この抵抗値の温度による変化は抵抗温度係数\(α_t\)を用いて計算することができ、次式で表すことができます。

\begin{eqnarray}
R_T&=&R_t+α_tR_t(T-t)\\
\\
&=&R_t\left\{1+α_t(T-t)\right\}\tag{1}
\end{eqnarray}

上式において、\(R_T\)、\(R_t\)、\(α_t\)は下記を示しています。

\(R_T\)：温度が\(T{\mathrm{[℃]}}\)に変化した時の抵抗値\({\mathrm{[Ω]}}\)
\(R_t\)：温度が\(t{\mathrm{[℃]}}\)の時の抵抗値\({\mathrm{[Ω]}}\)
\(α_t\)：温度が\(t{\mathrm{[℃]}}\)の時の抵抗温度係数\({\mathrm{[1/℃]}}\)

(1)式では、温度が\(t{\mathrm{[℃]}}\)の時の抵抗値を\(R_t{\mathrm{[Ω]}}\)として、温度が\(t{\mathrm{[℃]}}\)から\(T{\mathrm{[℃]}}\)に変化した時の抵抗値\(R_T{\mathrm{[Ω]}}\)を求めています。

「\(T-t\)」は「温度\(t{\mathrm{[℃]}}\)を基準として、温度がどれくらい変化したか」を示しており、温度が上昇すれば、\(T-t{\;}{\gt}{\;}0\)、温度が低下すれば\(T-t{\;}{\lt}{\;}0\)となります。

抵抗温度係数\(α_t\)は「\(1{\mathrm{[Ω]}}\)当たりの抵抗が\(1{\mathrm{[℃]}}\)上昇した時にどれくらい抵抗値が変化するのか」を表す係数です。抵抗温度係数\(α_t\)は物質によって異なり、

金、銀、銅、鉄などの金属導体の場合
- 抵抗温度係数\(α_t\)は正(プラス)
「ゲルマニウムやケイ素などの半導体」・「絶縁物」・「炭素」の場合
- 抵抗温度係数\(α_t\)は負(マイナス)

となります。例えば、銅の抵抗温度係数\(α_t\)は0.00393となります。

金属導体の場合、抵抗温度係数\(α_t\)が正なので、温度が\(t{\mathrm{[℃]}}\)から上昇すれば、「\(R_tα_t(T-t)\)」も正となります。そのため、温度が\(t{\mathrm{[℃]}}\)の時の抵抗値\(R_t{\mathrm{[Ω]}}\)に「\(R_tα_t(T-t)\)」を足した値が温度が\(T{\mathrm{[℃]}}\)の時の抵抗値\(R_T{\mathrm{[Ω]}}\)となります。

一方、半導体の場合、抵抗温度係数\(α_t\)が負なので、温度が\(t{\mathrm{[℃]}}\)から上昇すれば、「\(R_tα_t(T-t)\)」は負となります。そのため、温度が\(T{\mathrm{[℃]}}\)の時の抵抗値\(R_T{\mathrm{[Ω]}}\)は温度が\(t{\mathrm{[℃]}}\)の時の抵抗値\(R_t{\mathrm{[Ω]}}\)より小さくなります。

例題

温度\(t=25{\mathrm{[℃]}}\)の時、銅の抵抗値\(R_t\)が\(10{\mathrm{[Ω]}}\)でした。この銅が\(T=35{\mathrm{[℃]}}\)に上昇した時の抵抗値\(R_T\)は何Ωになるでしょうか。銅の抵抗温度係数\(α_t\)を0.00393として計算してみましょう。

解答

(1)式に各値を代入をすることで、\(T=35{\mathrm{[℃]}}\)に上昇した時の抵抗値\(R_T\)を求めることができます。

\begin{eqnarray}
R_T&=&R_t\left\{1+α_t(T-t)\right\}\\
\\
&=&10\left\{1+0.00393(35-25)\right\}\\
\\
&=&10\left\{1+0.00393×10\right\}\\
\\
&=&10\left\{1+0.0393\right\}\\
\\
&=&10×1.0393\\
\\
&=&10.393{\mathrm{[Ω]}}
\end{eqnarray}

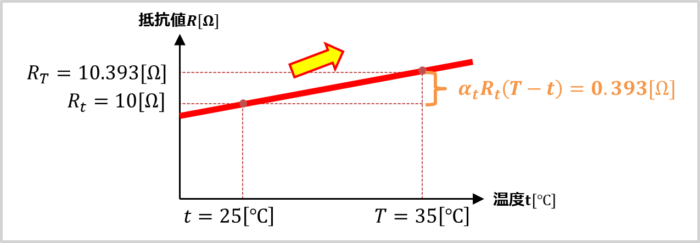
上式より、温度が\(10{\mathrm{[℃]}}\)上昇すると、抵抗値が\(0.393{\mathrm{[Ω]}}\)増加することが分かります。これをグラフで表すと下図のようになります。

ポイント

抵抗値の温度による変化を表す式
\begin{eqnarray}
R_T&=&R_t+α_tR_t(T-t)\\
\\
&=&R_t\left\{1+α_t(T-t)\right\}
\end{eqnarray}
金属導体の場合
- \(α_t\)が正なので、温度が上昇すると、抵抗値が大きくなる。
半導体の場合
- \(α_t\)が負なので、温度が上昇すると、抵抗値が小さくなる。

抵抗温度係数とは

(1)式を変形すると、抵抗温度係数\(α_t\)は次式で表すことができます。

\begin{eqnarray}
α_t=\frac{1}{R_t}×\frac{R_T-R_t}{T-t}{\mathrm{[1/℃]}}
\end{eqnarray}

抵抗温度係数\(α_t\)は「\(1{\mathrm{[Ω]}}\)当たりの抵抗が\(1{\mathrm{[℃]}}\)上昇した時にどれくらい抵抗値が変化するのか」を表す係数です。

したがって、\(α_t\)に\(R_t\)を掛けた\(α_tR_t\)は「\(R_t{\mathrm{[Ω]}}\)当たりの抵抗が\(1{\mathrm{[℃]}}\)上昇した時にどれくらい抵抗値が変化するのか」を表し、\(α_tR_t\)は抵抗値の温度変化の傾きを示します。

抵抗温度係数\(α_t\)は物質により異なります。下表に温度\(t=20{\mathrm{[℃]}}\)の時の抵抗温度係数\(α_t\)を示します。色々調べましたが、参考資料によって数値が微妙に異なるので、おおよその目安にしてください。

物質			\(α_t{\mathrm{[1/℃]}}\)
導体	銅	Cu	0.00393
	銀	Ag	0.00380
	金	Au	0.00340
	鉄	Fe	0.00500
	ニクロム	-	0.00019
	ニッケル	Ni	0.00600
	アルミニウム	Al	0.00390
	ビスマス	Bi	0.00400
	カドニウム	Cd	0.00380
	水銀	Hg	0.00089
	マグネシウム	Mg	0.00400
	モリブデン	Mo	0.00330
	鉛	Pb	0.00390
	パラジウム	Pd	0.00330
	白金	Pt	0.00300
	すず	Sn	0.00420
	タングステン	W	0.00450
	亜鉛	Zn	0.00370
半導体・その他	ゲルマニウム	Ge	－0.05000
	けい素	Si	－0.08000
	飽和食塩水	-	－0.00500

導線としてよく利用される銅は鉄と比較すると、抵抗温度係数\(α_t\)が低いことが分かります。また、ニクロムは温度変化に強いため、電熱線などに利用されています。

補足

抵抗温度係数は英語では「Temperature Coefficient of Resistance」と書きます。
英語の頭文字をとって抵抗温度係数のことを「TCR」と呼ぶこともあります。
抵抗温度係数の単位は\({\mathrm{[1/℃]}}\)以外にも\({\mathrm{[{\%}/℃]}}\)や\({\mathrm{[ppm/℃]}}\)で表す場合もあります。この場合、次式で計算することができます。
\begin{eqnarray}
α_t&=&\frac{1}{R_t}×\frac{R_T-R_t}{T-t}{\mathrm{[1/℃]}}\\
\\
&=&\frac{1}{R_t}×\frac{R_T-R_t}{T-t}×100{\mathrm{[{\%}/℃]}}\\
\\
&=&\frac{1}{R_t}×\frac{R_T-R_t}{T-t}×10^6{\mathrm{[ppm/℃]}}\\
\end{eqnarray}