『平均値』と『実効値』の違いについて！詳しく説明します！

この記事ではまず、『平均値』と『実効値』の違いについて説明した後に、『平均値』と『実効値』の特徴について詳しく説明します。

『平均値』と『実効値』の違い

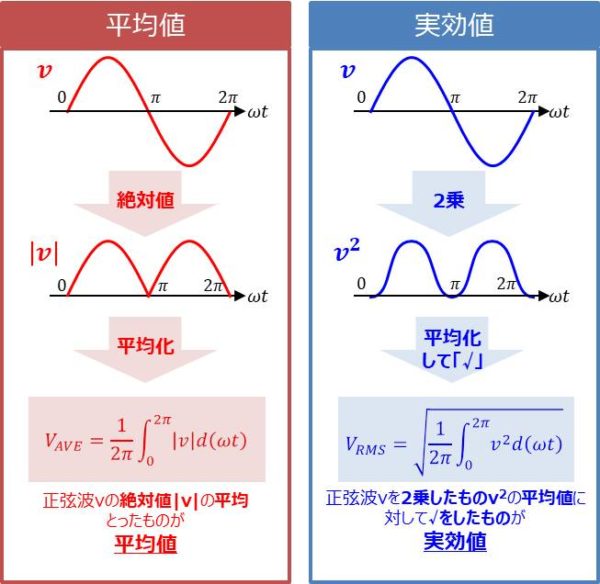
まず『平均値』と『実効値』の違いについて最初に説明します(後ほどそれぞれ詳しく説明します)。

正弦波\(v=V_M\sin{{\omega}t}\)を例にとって説明します。

平均値

「負」の値を「正」に置き換えて平均をとったものが平均値となります。言い換えれば、正弦波\(v\)の絶対値\(|v|\)の平均とったものが平均値\(V_{AVE}\)ということになります。

例えば、上図の場合には、平均値\(V_{AVE}\)は以下の値で表されます。

\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}|v|d({{\omega}t})\\
\\
&=&\displaystyle\frac{2V_M}{\pi}
\end{eqnarray}

実効値

正弦波\(v\)を2乗したもの\(v^2\)の平均値に対してルート(\(\sqrt{}\))をしたものが実効値となります。

例えば、上図の場合には、実効値\(V_{RMS}\)は以下の値で表されます。

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}v^2d({{\omega}t}})\\
\\
&=&\displaystyle\frac{V_M}{\sqrt{2}}
\end{eqnarray}

なお、上式の導出については以下の記事を参考にしてください。正弦波の平均値\(V_{AVE}\)が\(\displaystyle\frac{2V_M}{\pi}\)となる理由、正弦波の実効値\(V_{RMS}\)が\(\displaystyle\frac{V_M}{\sqrt{2}}\)となる理由を詳細に説明しています。

: 『正弦波』の実効値・平均値・波形率・波高率の求め方
続きを見る

『平均値』とは

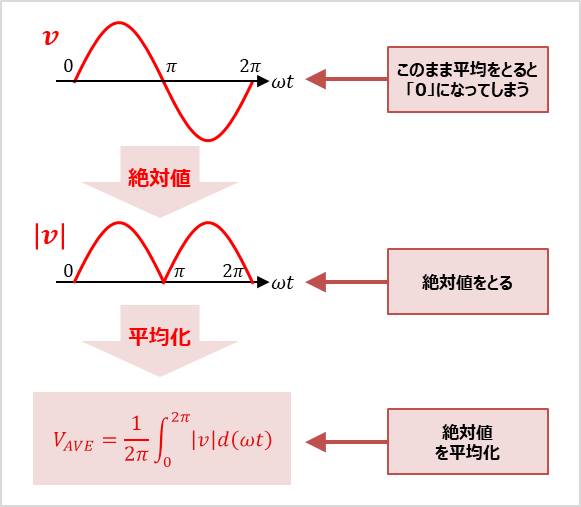
正弦波\(v=V_M\sin{{\omega}t}\)を例にとって考えます。

交流の「正」と「負」の平均をとると「0」になってしまうので、正弦波\(v\)の絶対値\(|v|\)の平均とったものを平均値\(V_{AVE}\)といいます。そのため、平均値\(V_{AVE}\)を求める式は以下の式で表されます。

\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}|v|d({{\omega}t})\\
\\
&=&\displaystyle\frac{2V_M}{\pi}
\end{eqnarray}

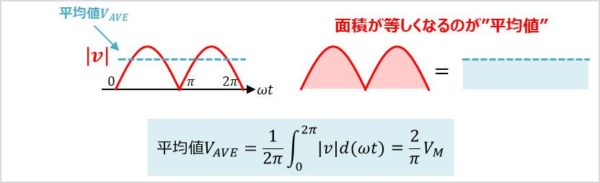
以下の図に示すように、上式は単純に、面積が等しくなることを示します。

補足

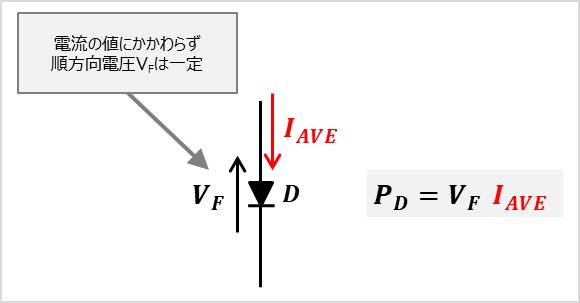
平均値\(V_{AVE}\)は電圧が電流にかかわらず一定となるもの(ダイオードの順方向電圧など)の損失(消費電力)を計算するときに用います。例えば、順方向電圧\(V_{F}\)のダイオードに流れる電流の平均値が\(I_{AVE}\)の場合、ダイオードでの損失(消費電力)\(P_{D}\)は以下の式で表されます。

\begin{eqnarray}
P_{D} &=& V_{F} I_{AVE}
\end{eqnarray}

『実効値』とは

正弦波\(v=V_M\sin{{\omega}t}\)を例にとって考えます。

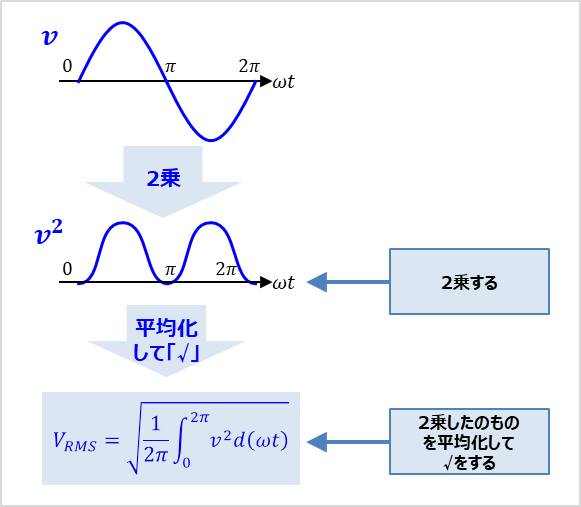
正弦波\(v\)を2乗したもの\(v^2\)の平均値に対してルート(\(\sqrt{}\))をしたものが実効値\(V_{RMS}\)となります。

そのため、実効値\(V_{RMS}\)を求める式は以下の式で表されます。

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}v^2d({{\omega}t}})\
\end{eqnarray}

では、なぜこのような式になるのでしょうか。

これは、実効値は「抵抗に直流電圧を加えた時と同じ電力を発生する電圧の値」だからです(少し難しいですね・・・)。

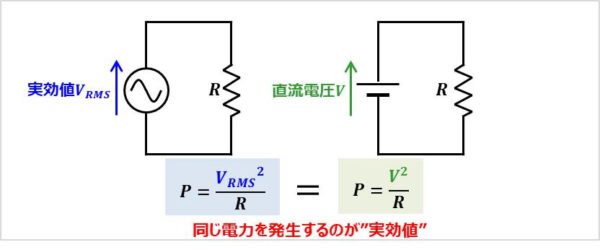
分かりやすく説明するために、ピーク値\(V_M\)が\(1{\mathrm{[V]}}\)、デューティ比\(D\)が\(0.5\)の方形波\(v\)を例にとって説明します。

方形波\(v\)の実効値\(V_{RMS}\)

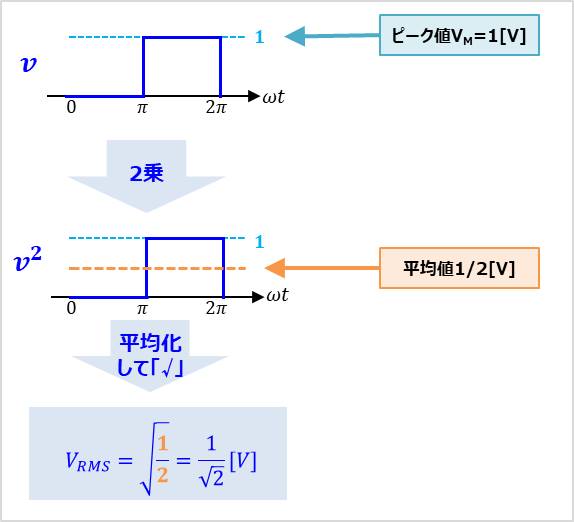
まず、方形波\(v\)の実効値\(V_{RMS}\)を求めてみます。

方形波\(v\)を2乗すると、周期の前半は\(0{\mathrm{[V]}}\)、周期の後半は\(1{\mathrm{[V]}}\)になります。

そのため、方形波\(v\)を2乗したもの\(v^2\)の平均値は\(\displaystyle\frac {1}{2}{\mathrm{[V]}}\)になります。

この平均値に対してルート(\(\sqrt{}\))を付けると\(\displaystyle\frac {1}{\sqrt{2}}{\mathrm{[V]}}\)になります。

すなわち、ピーク値\(V_M\)が\(1{\mathrm{[V]}}\)、デューティ比\(D\)が\(0.5\)の方形波\(v\)の実効値\(V_{RMS}\)は\(\displaystyle\frac {1}{\sqrt{2}}{\mathrm{[V]}}\)になります。

抵抗\(R\)に方形波\(v\)を加えた時の電力

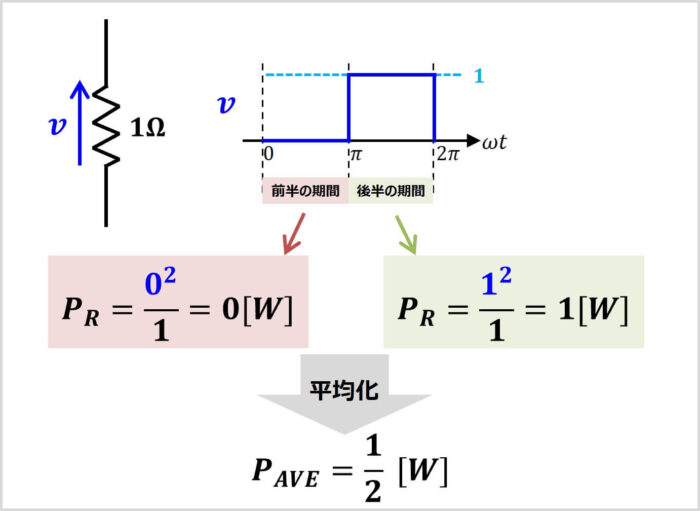
次に、抵抗に方形波\(v\)を加えた時の電力を求めてみます。

ピーク値\(V_M\)が\(1{\mathrm{[V]}}\)、デューティ比\(D\)が\(0.5\)の方形波\(v\)を\(1Ω\)の抵抗\(R\)に加えた時の電力\(P_R\)を考えてみます。

前半の\(0{\mathrm{[V]}}\)の期間で消費する電力は以下の値となります。

\begin{eqnarray}
P_R=\frac{V^2}{R}=\frac{0^2}{1}=0{\mathrm{[W]}}
\end{eqnarray}

後半の\(1{\mathrm{[V]}}\)の期間で消費する電力は以下の値となります。

\begin{eqnarray}
P_R=\frac{V^2}{R}=\frac{1^2}{1}=1{\mathrm{[W]}}
\end{eqnarray}

したがって、平均電力\(P_{AVE}\)は以下の式となります。

\begin{eqnarray}
P_{AVE}=\displaystyle\frac {1}{2}{\mathrm{[W]}}
\end{eqnarray}

抵抗\(R\)に直流電圧\(V\)を加えた時の電力

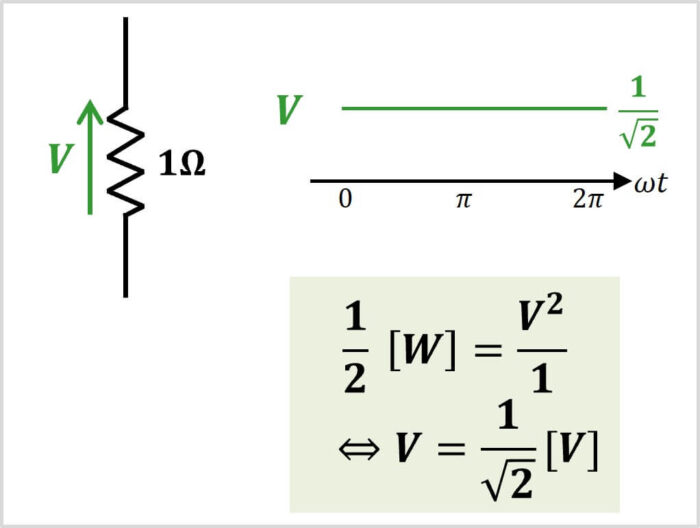
ここで、\(1Ω\)の抵抗\(R\)に直流電圧\(V\)を加えた時の電力が\(\displaystyle\frac {1}{2}{\mathrm{[W]}}\)になるときを考えると、

\begin{eqnarray}
\displaystyle\frac {1}{2}{\mathrm{[W]}}&=&\frac{V^2}{1}\\
\\
{\Leftrightarrow}V&=&\displaystyle\frac {1}{\sqrt{2}}{\mathrm{[V]}}
\end{eqnarray}

となります。これは、先ほど計算した実効値\(V_{RMS}\)と一致していることが分かります。

以上より、実効値\(V_{RMS}\)は抵抗に直流電圧\(V\)を加えた時と同じ電力を発生する電圧の値であることが分かります。

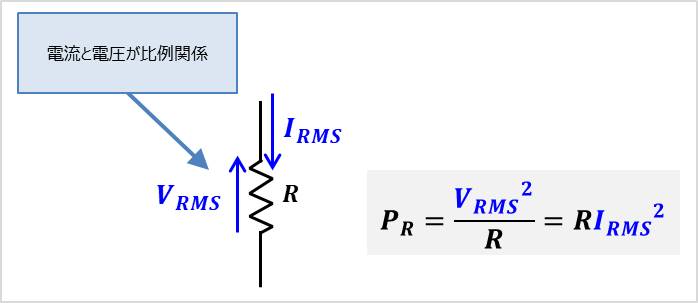
実効値は抵抗負荷の損失(消費電力)を計算するときに用いる

実効値は電圧と電流が比例する場合、すなわち抵抗負荷の損失(消費電力)を計算するときに用います。例えば、抵抗値\(R\)の抵抗にかかる電圧の実効値が\(V_{RMS}\)でその時に流れる電流の実効値が\(I_{RMS}\)の場合、抵抗での損失(消費電力)\(P_{R}\)は以下の式となります。

\begin{eqnarray}
P_{R}=\displaystyle\frac {{V_{RMS}}^2}{R}=R{I_{RMS}}^2
\end{eqnarray}