『台形波』の実効値・平均値の求め方

この記事では『台形波』について

などを図を用いて分かりやすく説明しています。

台形波の実効値・平均値

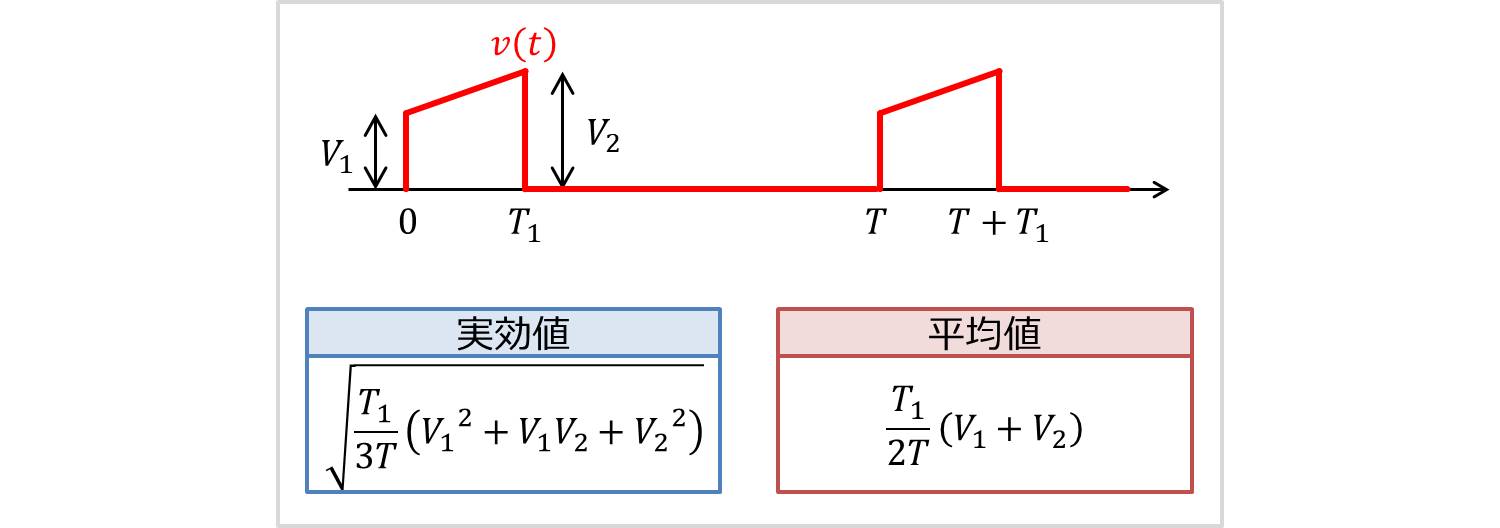
最初に台形波(短辺\(V_1\)、長辺\(V_2\)、オン時間\(T_1\)、周期\(T\))の実効値・平均値を上図に示します。
これから各値がどのように求まるのかを説明します(できるだけ途中式を多くするよう心がけています)。

台形波の波形式

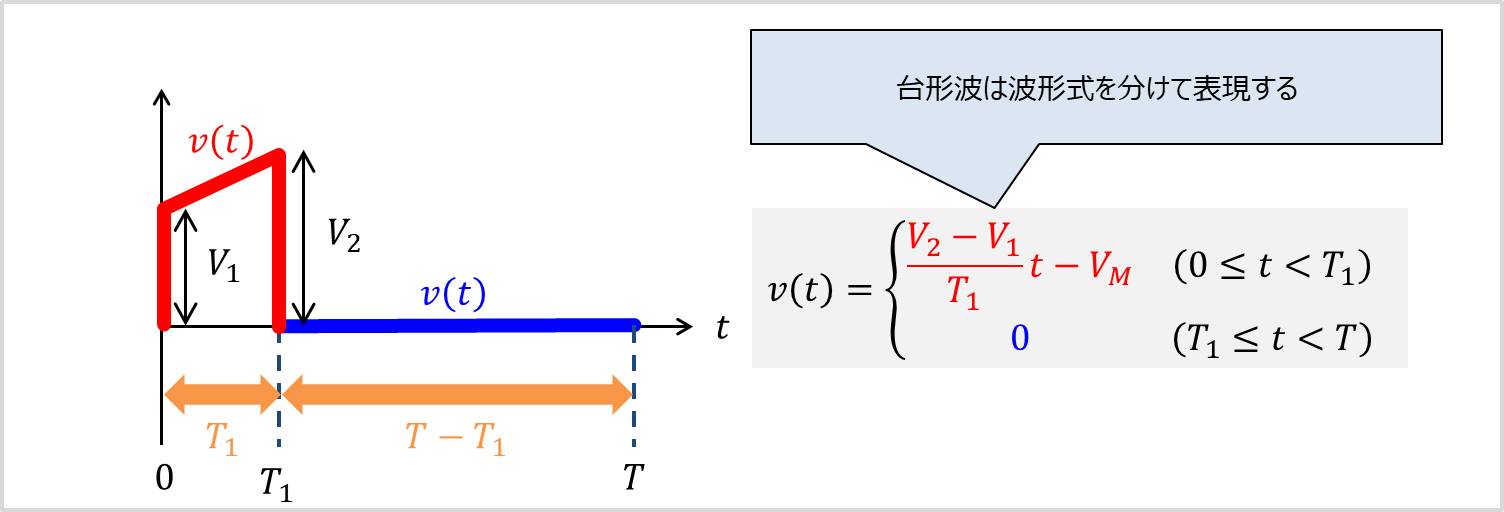
台形波の実効値・平均値を求めるためには、最初に台形波を式で表す必要があります。

台形波は2つの直線で表すことができます。

上図では台形波を赤色の直線と青色の直線で分けています。

赤色の直線の領域は「\(0 \leq t \lt T_1\)」、青色の直線の領域は「\(T_1 \leq t \lt T\)」となっています。

各直線の式を求めます。

赤色の直線

「\(0 \leq t \lt T_1\)」の領域が赤色の直線です。

赤色の直線の傾きは、時間\(T_1\)で\(V_1\)から\(V_2\)に増加しているため、
\begin{eqnarray}
赤色の直線の傾き=\displaystyle \frac{V_2-V_1}{T_1}
\end{eqnarray}
となります。

切片は、y軸と交わる点なので、
\begin{eqnarray}
赤色の直線の接点=V_1
\end{eqnarray}
となります。

そのため、赤色の直線の式は

で表すことができます。

青色の直線

「\(T_1 \leq t \lt T\)」の領域が青色の直線です。

青色の直線部分は常に"0"です。

したがって、青色の直線部分の式は

となります。

赤色の直線と青色の直線を合わせると、

となります。これが台形波の式です。

ここで、実効値・平均値を求める際には式を簡略化するために
\begin{eqnarray}
k = \displaystyle \frac{V_2-V_1}{T_1}
\end{eqnarray}
と置きます。

すると、台形波の式は

となります。

台形波の実効値

波形\(v(t)\)の実効値\(V_{RMS}\)は、\(v(t)\)を2乗して平均した値の平方根なので、

と表されます。

赤色の直線の領域は「\(0 \leq t \lt T_1\)」、青色の直線の領域は「\(T_1 \leq t \lt T\)」です。

絶対値を求める式において、赤色の直線と青色の直線を分けると、
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}v(t)^2dt+\displaystyle \int_{T_1}^{T}v(t)^2dt\right )}
\end{eqnarray}
となります。

このまま上式を解くと式が長くなり計算がしにくくなります。

そのため、
\begin{eqnarray}
X &=& \displaystyle \int_{0}^{T_1}v(t)^2dt\\
Y &=& \displaystyle \int_{T_1}^{T}v(t)^2dt\\
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \left(X+Y\right )}
\end{eqnarray}
と置き、\(X\)と\(Y\)の各値を別々に求めていきます。

\begin{eqnarray}
X&=&\displaystyle \int_{0}^{T_1}v(t)^2dt\\
&=&\displaystyle \int_{0}^{T_1}\left(kt+V_1 \right)^2dt \\
&=&\displaystyle \int_{0}^{T_1}\left(k^2t^2+2kV_1t+{V_1}^2 \right)dt \\
&=&\left[ \displaystyle \frac{1}{3}k^2t^3+kV_1t^2+{V_1}^2t \right]_{0}^{T_1}\\
&=&\displaystyle \frac{1}{3}k^2{T_1}^3+kV_1{T_1}^2+{V_1}^2{T_1}\\
&=&\displaystyle \frac{1}{3}\left(\displaystyle \frac{V_2-V_1}{T_1}\right )^2{T_1}^3+\left(\displaystyle \frac{V_2-V_1}{T_1}\right )V_1{T_1}^2+{V_1}^2{T_1}\\
&=&\displaystyle \frac{T_1}{3}\left({V_1}^2+{V_1}{V_2}+{V_2}^2\right )\\
Y&=&\displaystyle \int_{T_1}^{T}v(t)^2dt\\
&=&\displaystyle \int_{T_1}^{T}0^2dt\\
&=&0\\
\end{eqnarray}

以上より、三角波の実効値\(V_{RMS}\)は、

となります。

三角波の平均値

波形\(v(t)\)の平均値\(V_{AVE}\)は、\(v(t)\)の絶対値\(|v(t)|\)を平均した値なので、

と表されます。

この平均値を求める式は\(v(t)\)の絶対値\(|v(t)|\)を使用します。

台形波には負の領域がありませんので、『波形\(v(t)\)』と『波形\(v(t)\)の絶対値\(|v(t)|\)』は同じになります。

平均値を求める式において、赤色の直線と青色の直線を分けると、
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}|v(t)|dt+\displaystyle \int_{T_1}^{T}|v(t)|dt\right )
\end{eqnarray}
となります。

上式において、
\begin{eqnarray}
X &=& \displaystyle \int_{0}^{T_1}|v(t)|dt\\
Y &=& \displaystyle \int_{T_1}^{T}|v(t)|dt\\
V_{AVE} &=&\displaystyle\frac{1}{T} \left(X+Y\right )
\end{eqnarray}
と置き、\(X\)と\(Y\)の各値を別々に求めていきます。

\begin{eqnarray}
X &=& \displaystyle \int_{0}^{T_1}|v(t)|dt\\
&=& \displaystyle \int_{0}^{T_1}\left(kt+V_1\right )dt\\
&=&\left[ \displaystyle \frac{1}{2}kt^2+V_1t \right]_{0}^{T_1}\\
&=&\left( \displaystyle \frac{1}{2}k{T_1}^2+V_1{T_1} \right)\\
&=&\left( \displaystyle \frac{1}{2}\left(\displaystyle \frac{V_2-V_1}{T_1}\right ){T_1}^2+V_1{T_1} \right)\\
&=&\displaystyle \frac{{V_1+V_2}}{2}{T_1}\\
Y &=& \displaystyle \int_{T_1}^{T}|v(t)|dt\\
&=& \displaystyle \int_{T_1}^{T}0dt\\
&=& 0
\end{eqnarray}

以上より、台形波の平均値\(V_{AVE}\)は、

となります。

台形波の式の変換

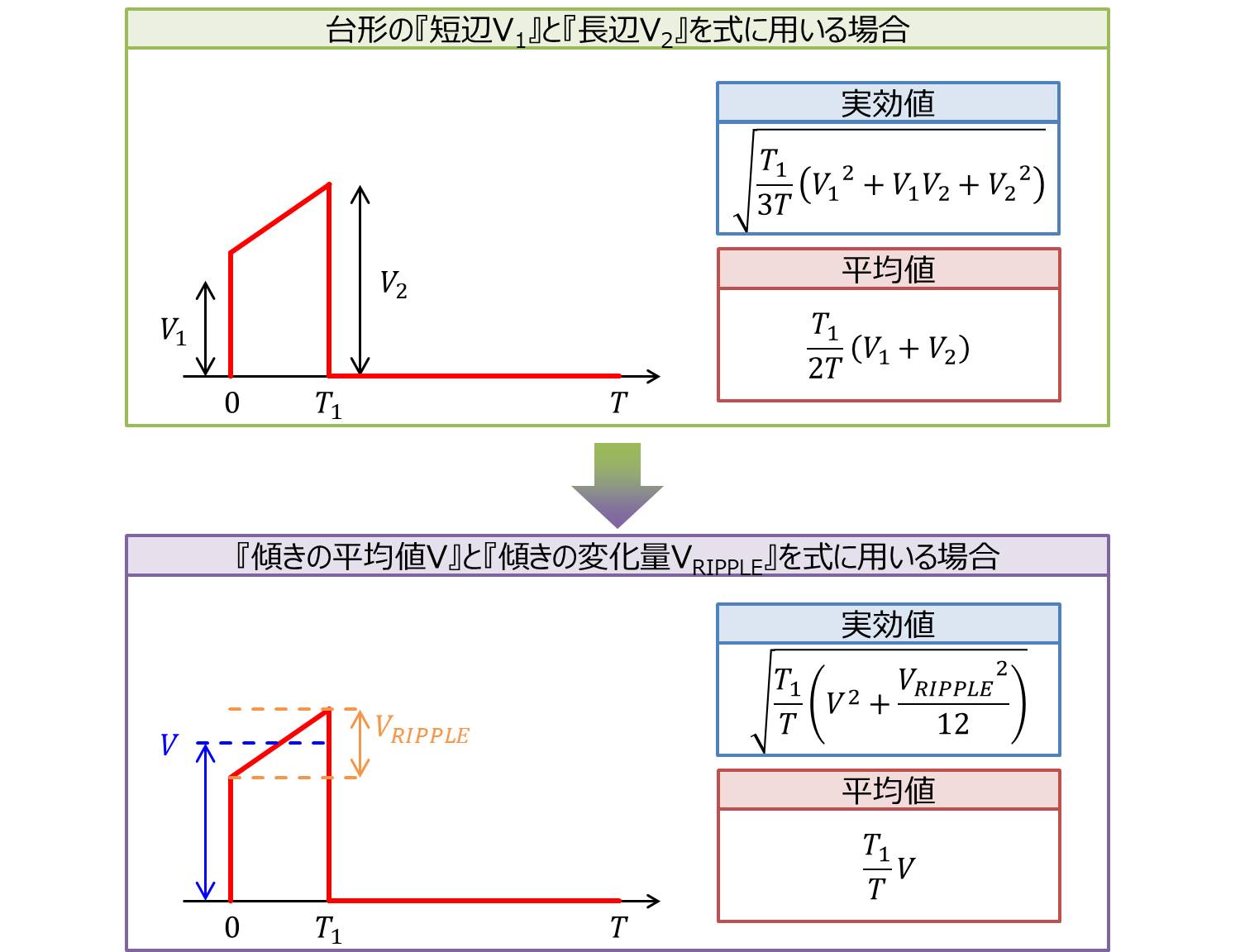
今までは短辺を\(V_1\)、長辺を\(V_2\)として台形波の実効値と平均値を求めてきました。

参考書によって様々なのですが、台形波の実効値・平均値を求める際に台形の短辺\(V_1\)、長辺を\(V_2\)を用いるのではなく、傾きの平均値\(V\)と傾きの変化量\(V_{RIPPLE}\)を用いて台形波の実効値と平均値を求めているのも見かけます。

傾きの平均値\(V\)と傾きの変化量\(V_{RIPPLE}\)を使用した場合の台形波の実効値・平均値も求めてみます。

台形の短辺\(V_1\)、長辺を\(V_2\)を傾きの平均値\(V\)と傾きの変化量\(V_{RIPPLE}\)で表すと以下の式になります。
\begin{eqnarray}
V_1 &=& V-\displaystyle \frac{1}{2}V_{RIPPLE}\\
V_2 &=& V+\displaystyle \frac{1}{2}V_{RIPPLE}
\end{eqnarray}

この式を先ほど求めた実効値と平均値の式に代入すると、
三角波の実効値\(V_{RMS}\)は、
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{T_1}{3T}\left({V_1}^2+{V_1}{V_2}+{V_2}^2\right )}\\
&=& \sqrt{\displaystyle\frac{T_1}{3T}\left(\left(V-\displaystyle \frac{1}{2}V_{RIPPLE}\right )^2+\left(V-\displaystyle \frac{1}{2}V_{RIPPLE}\right )\left( V+\displaystyle \frac{1}{2}V_{RIPPLE}\right )+\left( V+\displaystyle \frac{1}{2}V_{RIPPLE}\right )^2\right )}\\
&=&\sqrt{\displaystyle\frac{T_1}{T}\left(V^2+\displaystyle \frac{{V_{RIPPLE}}^2}{12}\right )}
\end{eqnarray}
となります。

三角波の平均値\(V_{AVE}\)は、
\begin{eqnarray}
V_{AVE} &=&\displaystyle \frac{{T_1}}{2T}\left(V_1+V_2\right)\\
&=&\displaystyle \frac{{T_1}}{2T}\left(\left(V-\displaystyle \frac{1}{2}V_{RIPPLE}\right )+\left( V+\displaystyle \frac{1}{2}V_{RIPPLE}\right )\right)\\
&=&\displaystyle \frac{{T_1}}{2}V
\end{eqnarray}
となります。