この記事では『パルス波』について
- 実効値・平均値・波形率・波高率の求め方
などを図を用いて分かりやすく説明しています。
パルス波の実効値・平均値
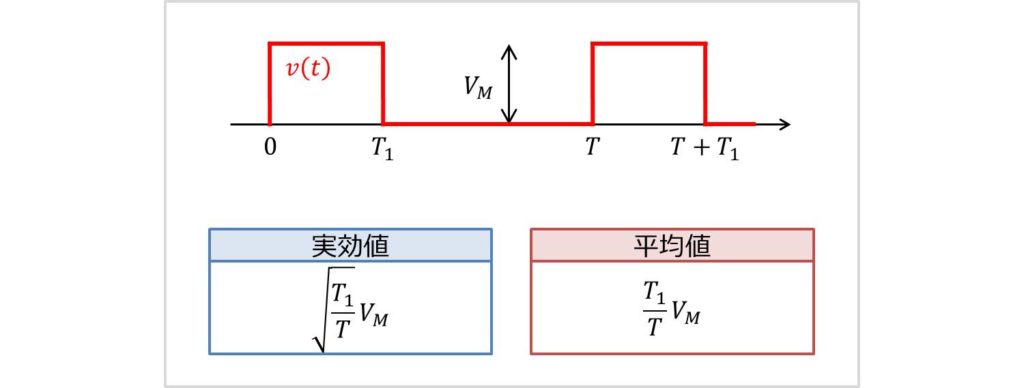
最初にパルス波(最大値\(V_M\)、オン時間\(T_1\)、周期\(T\))の実効値・平均値を上図に示します。
これから各値がどのように求まるのかを説明します(できるだけ途中式を多くするよう心がけています)。
パルス波の波形式
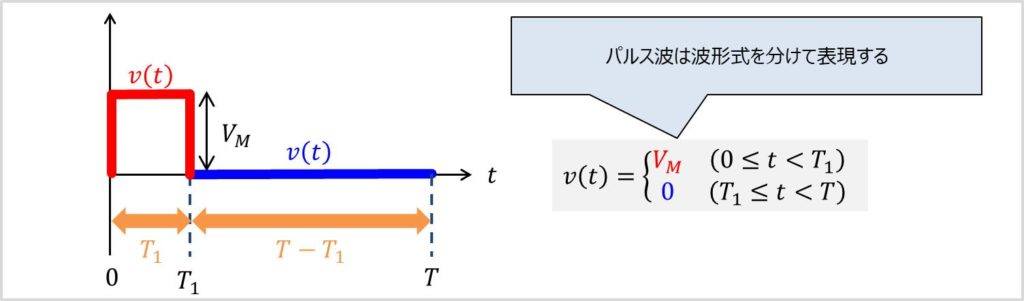
パルス波の実効値・平均値を求めるためには、最初にパルス波を式で表す必要があります。
パルス波は2つの直線で表すことができます。
上図ではパルス波を赤色の直線と青色の直線で分けています。
赤色の直線の領域は「\(0 \leq t \lt T_1\)」、青色の直線の領域は「\(T_1 \leq t \lt T\)」となっています。
各直線の式を求めます。
赤色の直線
「\(0 \leq t \lt T_1\)」の領域が赤色の直線です。
赤色の直線は、時間\(T_1\)の間、常に\(V_M\)となっています。
そのため、赤色の直線の式は
v(t)=V_M
\end{eqnarray}
で表すことができます。
青色の直線
「\(T_1 \leq t \lt T\)」の領域が青色の直線です。
青色の直線は、時間\(T_1\)の間、常に\(0\)となっています。
そのため、青色の直線の式は
v(t)=0
\end{eqnarray}
で表すことができます。
赤色の直線と青色の直線を合わせると、
v(t) = \begin{cases}
V_M & \left(0 \leq t \lt T_1\right) \\
0 & \left(T_1 \leq t \lt T\right)
\end{cases}
\end{eqnarray}
となります。
これがパルス波の波形式です。
パルス波の実効値
波形\(v(t)\)の実効値\(V_{RMS}\)は、\(v(t)\)を2乗して平均した値の平方根なので、
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}v(t)^2dt}
\end{eqnarray}
と表されます。
絶対値を求める式において、赤色の直線と青色の直線を分けると、
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}v(t)^2dt+\displaystyle \int_{T_1}^{T}v(t)^2dt\right )}
\end{eqnarray}
となります。
「\(T_1 \leq t \lt T\)」の領域では\(v(t)=0\)なので上式は、
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}v(t)^2dt+\displaystyle \int_{T_1}^{T}0\right )}\\
&=& \sqrt{\displaystyle\frac{1}{T} \displaystyle \int_{0}^{T_1}v(t)^2dt}
\end{eqnarray}
となります。
上式において、\(v(t)=V_M\)を代入すると、
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T_1} \displaystyle \int_{0}^{T}V_M^2dt}
\end{eqnarray}
となります。\(V_M^2\)は時間\(t\)によって変化する変数ではなく定数なので積分の外に出すことができます。
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T_1} V_M^2\displaystyle \int_{0}^{T}1dt}\\
&=& V_M\sqrt{\displaystyle\frac{1}{T_1} \displaystyle \int_{0}^{T}1dt}
\end{eqnarray}
上式を計算すると、
\begin{eqnarray}
V_{RMS} &=& V_M\sqrt{\displaystyle\frac{1}{T} \left[t\right]_{0}^{T_1}}\\
&=& V_M\sqrt{\displaystyle\frac{1}{T} \left(T_1-0\right)}\\
&=& \sqrt{\displaystyle\frac{T_1}{T}}V_M
\end{eqnarray}
以上より、パルス波の実効値\(V_{RMS}\)は、
V_{RMS} =\sqrt{\displaystyle\frac{T_1}{T}}V_M
\end{eqnarray}
となります。
パルス波の平均値
波形\(v(t)\)の平均値\(V_{AVE}\)は\(v(t)\)の絶対値\(|v(t)|\)を平均した値なので、
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}|v(t)|dt
\end{eqnarray}
と表されます。
この平均値を求める式は『\(v(t)\)の絶対値\(|v(t)|\)』を使用します。
そのため、波形のマイナスの領域はプラスになるように変換する必要があります。
パルス波の場合はマイナスの領域はないため、『\(v(t)\)の式』と『\(v(t)\)の絶対値\(|v(t)|\)の式』は同じになります。
したがって、\(v(t)\)の絶対値\(|v(t)|\)の式は
|v(t)| = \begin{cases}
V_M & \left(0 \leq t \lt T_1\right) \\
0 & \left(T_1 \leq t \lt T\right)
\end{cases}
\end{eqnarray}
となります。
平均値を求める式において、赤色の直線と青色の直線を分けると、
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}|v(t)|dt+\displaystyle \int_{T_1}^{T}|v(t)|dt\right )
\end{eqnarray}
となります。
「\(T_1 \leq t \lt T\)」の領域では\(|v(t)|=0\)なので上式は、
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}|v(t)|dt+\displaystyle \int_{T_1}^{T}0dt\right )\\
&=&\displaystyle\frac{1}{T} \displaystyle \int_{0}^{T_1}|v(t)|dt\\
\end{eqnarray}
となります。
上式において、\(|v(t)|=V_M\)を代入すると、
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T_1}V_Mdt\\
&=& \displaystyle\frac{1}{T} V_M\displaystyle \int_{0}^{T_1}1dt\\
&=& \displaystyle\frac{1}{T}V_M \left[t\right]_{0}^{T_1}\\
&=& \displaystyle\frac{1}{T}V_M \left(T_1-0\right)\\
&=&\displaystyle\frac{T_1}{T}V_M
\end{eqnarray}
となります。
以上よりパルス波の平均値\(V_{AVE}\)は、
V_{AVE} &=& \displaystyle\frac{T_1}{T}V_M
\end{eqnarray}
となります。
