今回は正弦波、方形波、三角波、パルス波など様々な波形の『実効値・平均値・波形率・波高率』をまとめました。
これから各波形について紹介します。
様々な波形の『実効値・平均値・波形率・波高率』のまとめ
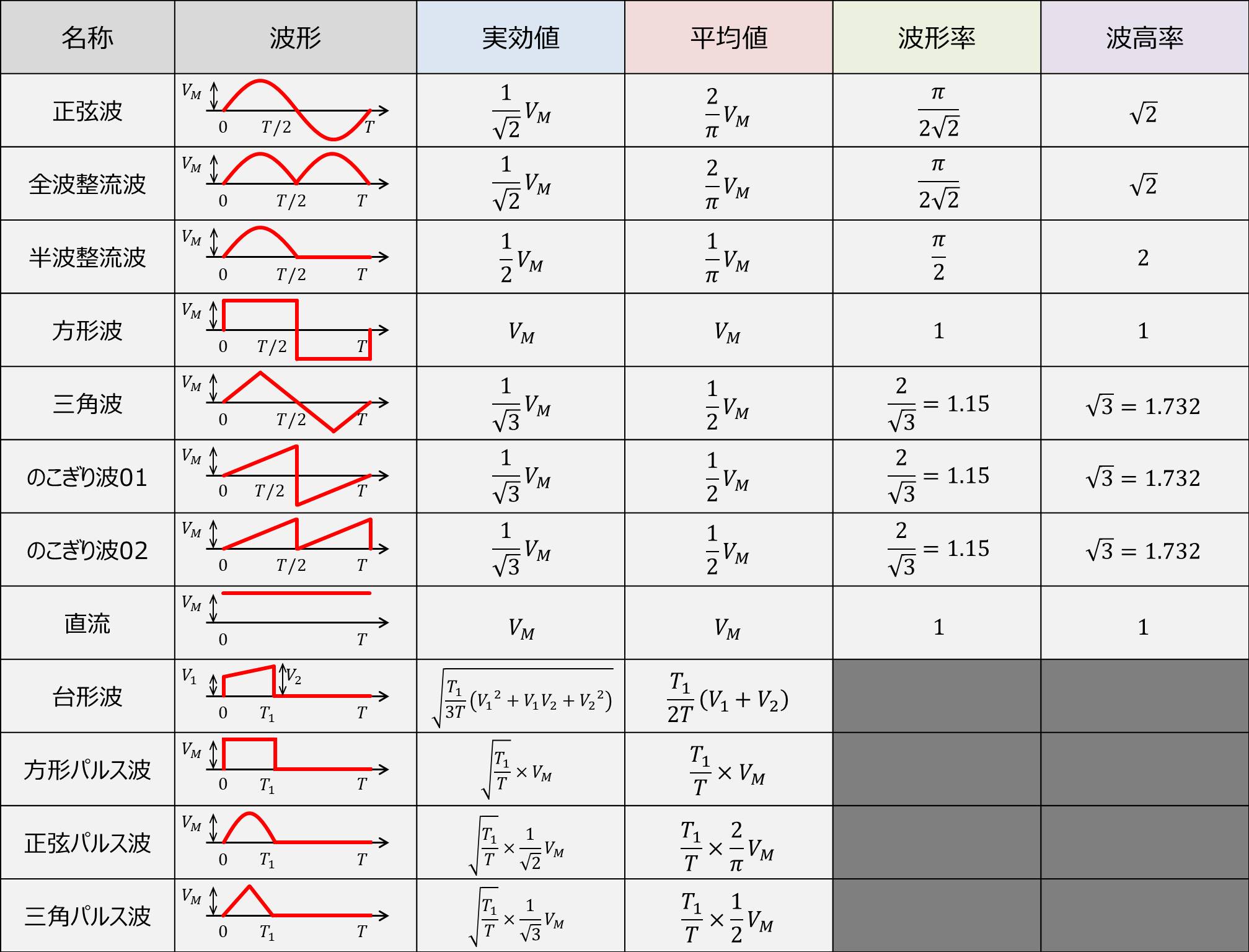
『実効値・平均値・波形率・波高率』をまとめると上表のようになります。
下から4つの波形はパルス波なので、波形率と波高率がありません。
正弦波や方形波といった周期波形に関しては波形率と波高率を求めています。
これから各波形を波形の外形で分類し、その分類毎に特徴を説明します。
分類は以下のように行っています。
- 正弦波関係
- 三角波関係
- 方形波関係
- その他
正弦波、全波整流波、半波整流波、正弦パルス波
三角波、のこぎり波01、のこぎり波02、三角パルス波
方形波、直流、方形パルス波
台形波
正弦波関係の『実効値・平均値・波形率・波高率』

上に正弦波、全波整流波、半波整流波、正弦パルス波の『実効値・平均値・波形率・波高率』をまとめています。
正弦波の実行値は\(V_{RMS}=\displaystyle\frac{1}{\sqrt{2}}V_M\)、平均値は\(V_{AVE}=\displaystyle\frac{2}{\pi}V_M\)です。
全波整流波の実行値と平均値は正弦波と同じ値となります。
半波整流波・正弦パルス波の実行値と平均値を求める方法は簡単です。
周期を\(T\)、オン時間を\(T_1\)とすると、
以下の方法で求めることができます。
ポイント
正弦波の実行値\(\displaystyle\frac{1}{\sqrt{2}}V_M\)に、\(\sqrt{\displaystyle\frac{オン時間}{周期}}\)を掛ける
正弦波の平均値\(\displaystyle\frac{2}{\pi}V_M\)に、\(\displaystyle\frac{オン時間}{周期}\)を掛ける
ことで求めることができます。
この後に出てくる三角波や正弦波も同じ要領で求めることができます。
周期を\(T\)、半波整流波のオン時間を\(\displaystyle\frac{T}{2}\)、正弦パルス波のオン時間を\(T_1\)とすると、
\begin{eqnarray}
半波整流波の実行値&=&\sqrt{\displaystyle\frac{\displaystyle\frac{T}{2}}{T}}×\displaystyle\frac{1}{\sqrt{2}}V_M=\displaystyle\frac{1}{2}V_M\\
正弦パルス波の実行値&=&\sqrt{\displaystyle\frac{T_1}{T}}×\displaystyle\frac{1}{\sqrt{2}}V_M\\
半波整流波の平均値&=&\displaystyle\frac{\displaystyle\frac{T}{2}}{T}×\displaystyle\frac{2}{\pi}V_M=\displaystyle\frac{1}{\pi}V_M\\
正弦パルス波の平均値&=&\displaystyle\frac{T_1}{T}×\displaystyle\frac{2}{\pi}V_M
\end{eqnarray}
となります。
各波形の細かい計算方法については以下を参照してください。
『正弦波』の実効値・平均値・波形率・波高率の求め方
『全波整流波』の実効値・平均値・波形率・波高率の求め方
『半波整流波』の実効値・平均値・波形率・波高率の求め方
三角波関係の『実効値・平均値・波形率・波高率』
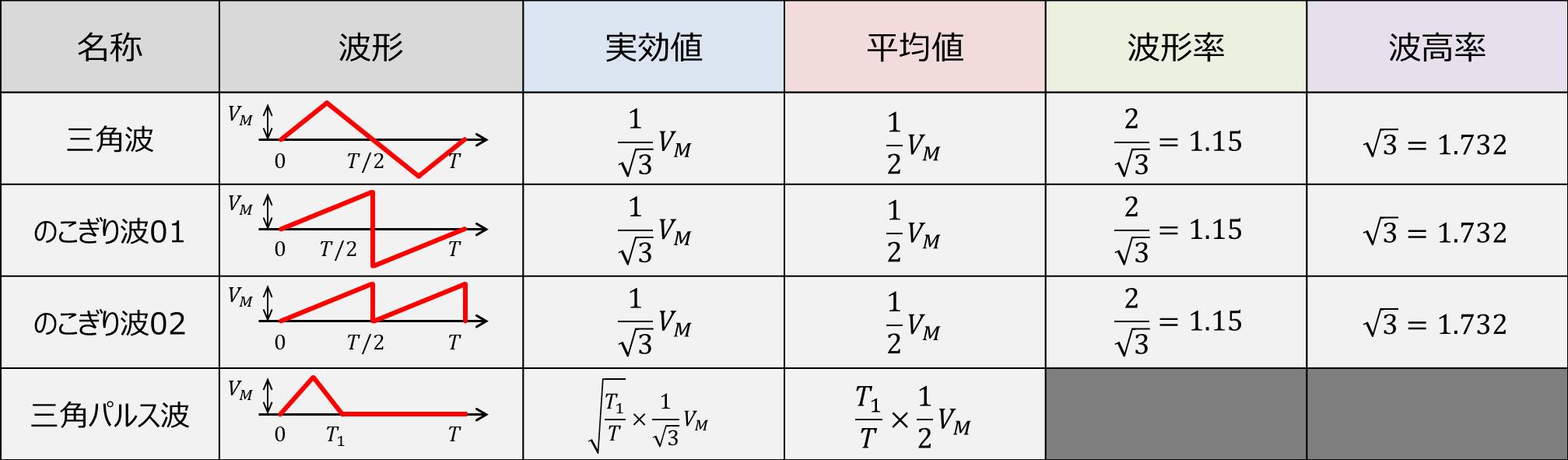
上に三角波、のこぎり波01、のこぎり波02、三角パルス波の『実効値・平均値・波形率・波高率』をまとめています。
三角波の実行値は\(V_{RMS}=\displaystyle\frac{1}{\sqrt{3}}V_M\)、平均値は\(V_{AVE}=\displaystyle\frac{1}{2}V_M\)です。
のこごり波01とのこごり波02の実行値と平均値は正弦波と同じ値となります。
三角パルス波の実行値と平均値を求める方法は正弦波で求めた方法と同じです。
周期を\(T\)、三角パルス波のオン時間を\(T_1\)とすると、
\begin{eqnarray}
三角パルス波の実行値&=&\sqrt{\displaystyle\frac{T_1}{T}}×\displaystyle\frac{1}{\sqrt{3}}V_M\\
三角パルス波の平均値&=&\displaystyle\frac{T_1}{T}×\displaystyle\frac{1}{2}V_M
\end{eqnarray}
となります。
各波形の細かい計算方法については以下を参照してください。
『三角波』の実効値・平均値・波形率・波高率の求め方
方形波関係の『実効値・平均値・波形率・波高率』
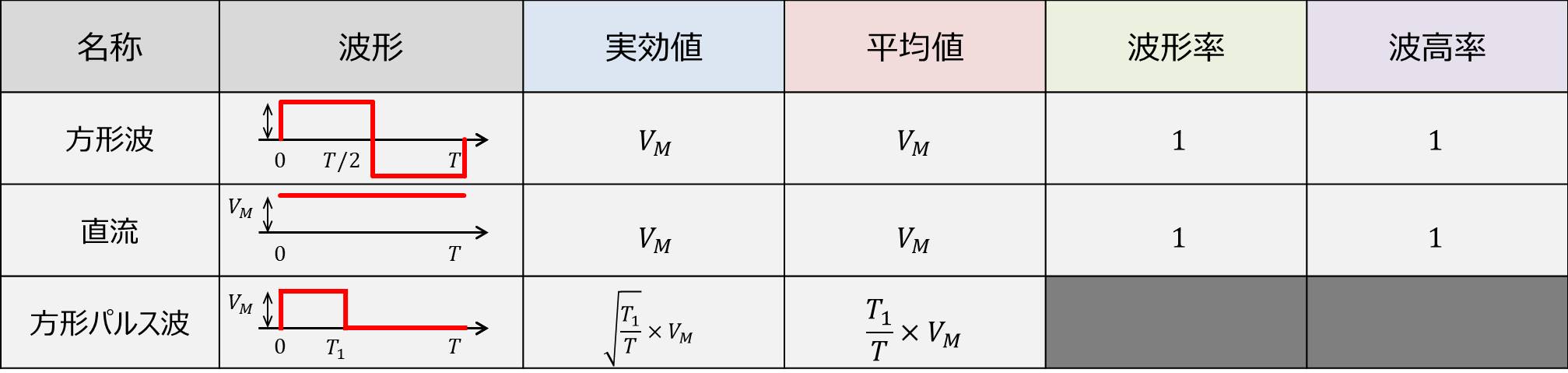
上に方形波、直流、方形パルス波の『実効値・平均値・波形率・波高率』をまとめています。
方形波の実行値は\(V_{RMS}=V_M\)、平均値は\(V_{AVE}=V_M\)です。
直流の実行値と平均値は正弦波と同じ値となります。
方形パルス波の実行値と平均値を求める方法は正弦波で求めた方法と同じです。
周期を\(T\)、方形パルス波のオン時間を\(T_1\)とすると、
\begin{eqnarray}
方形パルス波の実行値&=&\sqrt{\displaystyle\frac{T_1}{T}}×V_M\\
方形パルス波の平均値&=&\displaystyle\frac{T_1}{T}×V_M
\end{eqnarray}
となります。
各波形の細かい計算方法については以下を参照してください。
『方形波』の実効値・平均値・波形率・波高率の求め方
『直流』の実効値・平均値・波形率・波高率の求め方
『パルス波』の実効値・平均値・波形率・波高率の求め方
その他波形の『実効値・平均値・波形率・波高率』

上に台形波の『実効値・平均値・波形率・波高率』をまとめています。
台形波はパルス波なので、波形率と波高率がありません。
細かい計算方法については以下を参照してください。
『台形波』の実効値・平均値の求め方






