テブナンの定理とは？分かりやすく説明します！

この記事では『テブナンの定理』について

テブナンの定理とは
テブナンの定理を用いて電圧を求める手順

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

テブナンの定理とは

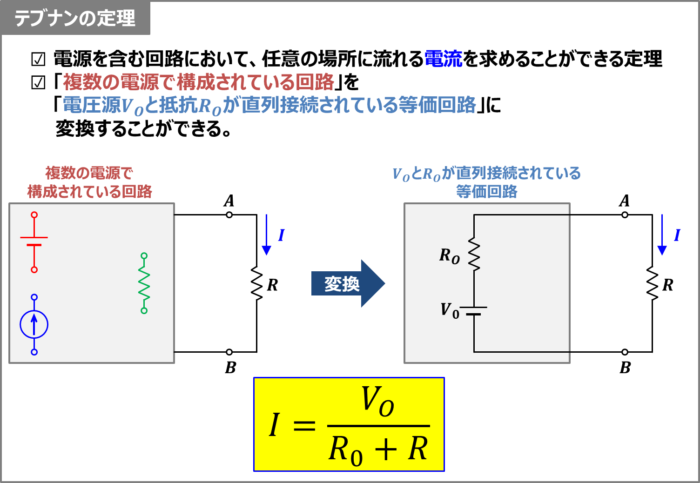
テブナンの定理は、電源(電圧源、電流源)を含む回路において、任意の場所に流れる電流を求めることができる定理です。

テブナンの定理を用いれば、上図に示すような「複数の電源で構成されている回路」を「電圧源\(V_O\)と抵抗\(R_O\)が直列接続されている等価回路」に変換することができます。この時、抵抗\(R\)に流れる電流\(I\)は次式で求めることができます。

\begin{eqnarray}
I=\frac{V_O}{R_O+R}\tag{1}
\end{eqnarray}

上式において、\(R_O\)、\(V_O\)、\(R\)は以下の意味となっています。

\(R_O\)

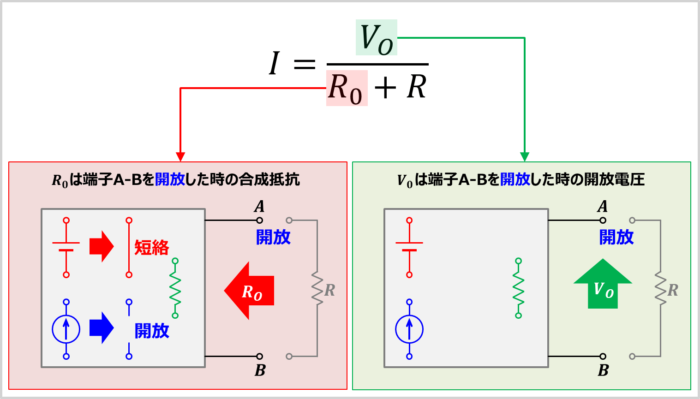
\(R_O\)は端子A-Bを開放した時の合成抵抗です。合成抵抗\(R_O\)を求める際には、電圧源は短絡し、電流源は開放させます。

\(V_O\)

\(V_O\)は端子A-Bを開放した時の開放電圧です。

\(R\)

\(R\)は抵抗\(R\)の抵抗値です。

では次に、実際の回路で抵抗\(R\)に流れる電流\(I\)をテブナンの定理を用いて求めてみましょう。

補足

テブナンの定理は「鳳(ほう)-テブナンの定理」、「ヘルムホルツ・テブナンの定理」、「等価電圧源の定理」とも呼ばれています。
テブナンの定理は英語では「Thevenin's theorem」と書きます。
テブナンの定理の「テブナン」はフランスの電気通信技術者「レオン・シャルル・テブナン(Léon Charles Thévenin)」が由来です。
「鳳(ほう)-テブナンの定理」の「鳳(ほう)」は1922年に交流電源に場合にも「テブナンの定理」が成立することを発表した東京帝国大学工学部電気工学科(当時)の「鳳秀太郎教授」が由来です。

テブナンの定理を用いて電流を求める手順

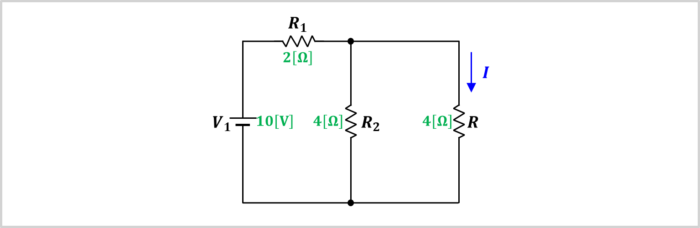
では実際に、上図に示している回路(電圧源\(V_1\)、抵抗\(R_1\),\(R_2\),\(R\)で構成)において、抵抗\(R\)に流れる電流\(I\)を求めてみましょう。

抵抗\(R\)に流れる電流\(I\)は下記の手順(ステップ1～5)で求めることができます。

テブナンの定理を用いて電圧を求める手順

流れる電流\(I\)を求めたい抵抗\(R\)の両端に端子Aと端子Bを割り当てる
端子A-B間を開放した時の合成抵抗\(R_O\)を求める
端子A-B間を開放した時の開放電圧\(V_O\)を求める
電圧源\(V_O\)と合成抵抗\(R_O\)の等価回路に変換する
テブナンの定理の公式に\(R_O\),\(V_O\),\(R\)を代入して、電流\(I\)を求める

流れる電流\(I\)を求めたい抵抗\(R\)の両端に端子Aと端子Bを割り当てる

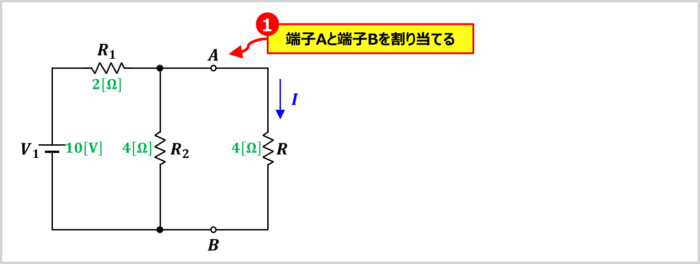
上図に示すように、抵抗\(R\)の両端に端子Aと端子Bを割り当てます。

端子A-B間を開放した時の合成抵抗\(R_O\)を求める

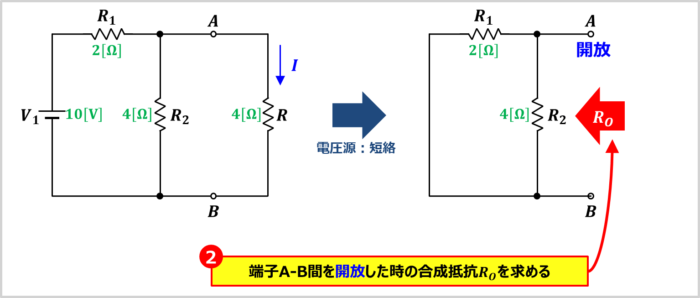
端子A-B間を開放した時の合成抵抗\(R_O\)を求めます。合成抵抗\(R_O\)を求める際には、電圧源は短絡し、電流源は開放させて求めます。

上図に示している回路の場合、電圧源を短絡させると、抵抗\(R_1\)と抵抗\(R_2\)が並列接続された回路となります。並列接続された回路の場合、合成抵抗\(R_O\)の逆数\(\displaystyle\frac{1}{R_O}\)は「各々の抵抗の逆数の和」になるため、次式で表されます。

\begin{eqnarray}
\frac{1}{R_O}&=&\frac{1}{R_1}+\frac{1}{R_2}\\
\\
{\Leftrightarrow}R_O&=&\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}}=\frac{1}{\displaystyle\frac{1}{2}+\displaystyle\frac{1}{4}}=\frac{1}{\displaystyle\frac{2+1}{4}}=\frac{4}{3}{\mathrm{[{\Omega}]}}\tag{2}\\
\end{eqnarray}

端子A-B間を開放した時の開放電圧\(V_O\)を求める

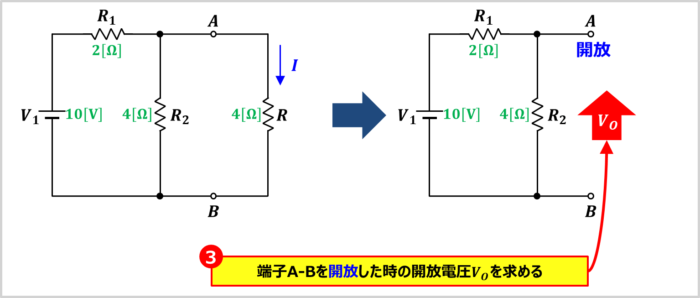
端子A-B間を開放した時の開放電圧\(V_O\)を求めます。

端子A-B間を開放すると、上図に示すような回路になります。開放電圧\(V_O\)は電圧源\(V_1\)を抵抗\(R_1\)と抵抗\(R_2\)で分圧した値になるため、次式で表されます。

\begin{eqnarray}
V_O=\frac{R_2}{R_1+R_2}V_1=\frac{4}{2+4}×10=\frac{2}{3}×10=\frac{20}{3}{\mathrm{[V]}}\tag{3}
\end{eqnarray}

電圧源\(V_O\)と合成抵抗\(R_O\)の等価回路に変換する

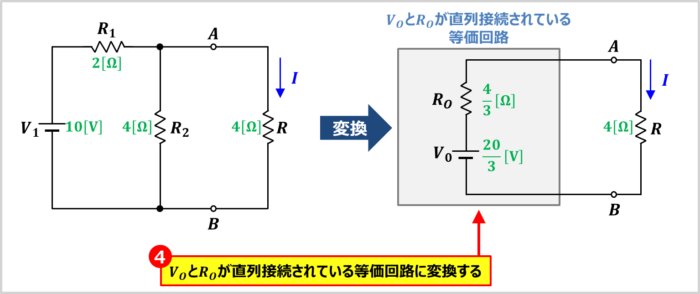
ステップ2,3で求めた合成抵抗\(R_O\)と開放電圧\(V_O\)を用いると、上図に示すような「電圧源\(V_O\)と抵抗\(R_O\)が直列接続されている等価回路」に変換することができ、複雑な回路をシンプルにすることができます。

補足

テブナンの定理を用いて変換した等価回路は「テブナンの等価回路」や「等価電圧源表示」と呼ばれています。

テブナンの定理の公式に\(R_O\),\(V_O\),\(R\)を代入して、電流\(I\)を求める

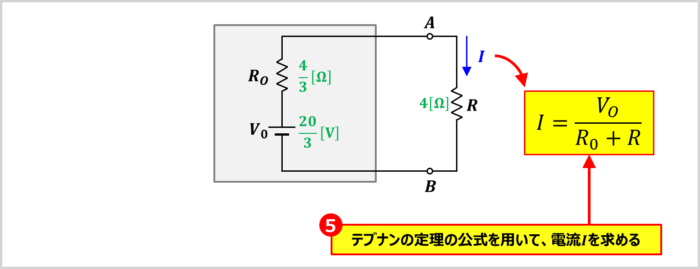
「電圧源\(V_O\)と抵抗\(R_O\)が直列接続されている等価回路」より、抵抗\(R\)に流れる電流\(I\)は次式で表されます。

\begin{eqnarray}
I=\frac{V_O}{R_O+R}\tag{4}
\end{eqnarray}

上式に、各値を代入すると、抵抗\(R\)に流れる電流\(I\)は以下の値となります。

\begin{eqnarray}
I=\frac{V_O}{R_O+R}=\frac{\displaystyle\frac{20}{3}}{\displaystyle\frac{4}{3}+4}=\frac{20}{4+12}=\frac{5}{4}=1.25{\mathrm{[A]}}\tag{5}
\end{eqnarray}

なお、抵抗\(R\)にかかる電圧\(V\)はオームの法則より以下の値となります。

\begin{eqnarray}
V=R×I=4×1.25=5{\mathrm{[V]}}\tag{6}
\end{eqnarray}

【関連記事】ノートンの定理

なお、抵抗\(R\)にかかる電圧\(V\)は『ノートンの定理』でも求めることができます。

『ノートンの定理』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。

ノートンの定理とは？分かりやすく説明します！
ノートンの定理の例題
ノートンの定理の証明