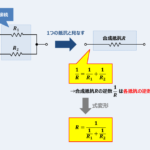
この記事では抵抗の『並列接続』と『和分の積』について
- 和分の積とは
- 和分の積の『証明』と『注意点』
- 和分の積は『抵抗』以外にも『コンデンサ』と『インダクタ』にも使用できること
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
和分の積とは
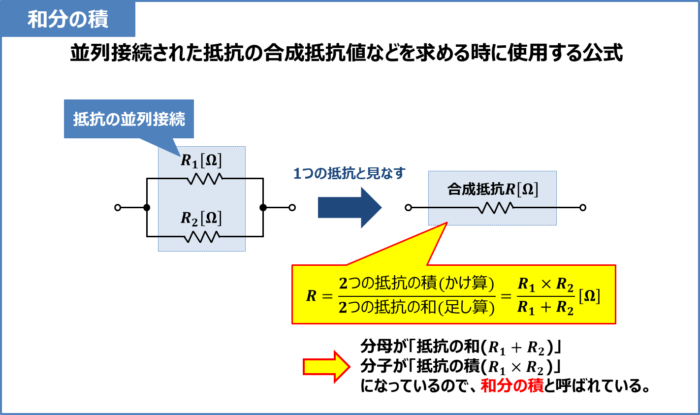
和分の積は、並列接続された抵抗の合成抵抗値などを求める時に使用する公式です。
例えば、上図に示すように「\(R_1{\mathrm{[{\Omega}]}}\)の抵抗」と「\(R_2{\mathrm{[{\Omega}]}}\)の抵抗」が並列接続されている時、合成抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表されます。
\begin{eqnarray}
R=\frac{\mbox{2つの抵抗の積(かけ算)}}{\mbox{2つの抵抗の和(足し算)}}=\frac{R_1×R_2}{R_1+R_2}{\mathrm{[{\Omega}]}}\tag{1}
\end{eqnarray}
(1)式から分かるように、分母が「抵抗の和(\(R_1+R_2\))」、分子が「抵抗の積(\(R_1×R_2\))」になっているので、和分の積と呼ばれています。
あわせて読みたい
並列接続された抵抗の合成抵抗の『求め方』と『例題』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-

抵抗の並列接続!合成抵抗の『式』や『証明』などを解説!
続きを見る
和分の積の『証明』
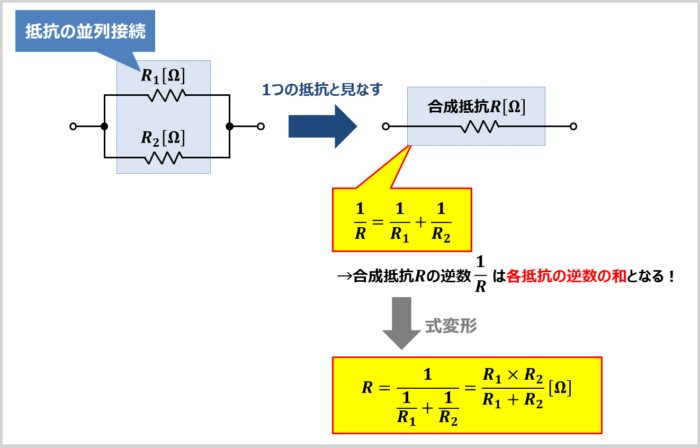

「\(R_1{\mathrm{[{\Omega}]}}\)の抵抗」と「\(R_2{\mathrm{[{\Omega}]}}\)の抵抗」が並列接続されている時、合成抵抗\(R\)の逆数\(\displaystyle\frac{1}{R}\)は各抵抗の逆数の和で計算することができ、次式で表されます。
\begin{eqnarray}
\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\tag{2}
\end{eqnarray}
上式を変形すると、合成抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表されます。
\begin{eqnarray}
R=\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}}{\mathrm{[{\Omega}]}}\tag{3}
\end{eqnarray}
(3)式において、分母と分子に「\(R_1×R_2\)」を掛けると、次式となります。
\begin{eqnarray}
R=\frac{R_1×R_2}{\displaystyle\frac{R_1×R_2}{R_1}+\displaystyle\frac{R_1×R_2}{R_2}}{\mathrm{[{\Omega}]}}\tag{4}
\end{eqnarray}
(4)式において、分母の箇所を約分すると、次式のようになり、和分の積の公式を導出することができます。
\begin{eqnarray}
R=\frac{R_1×R_2}{R_2+R_1}=\frac{R_1×R_2}{R_1+R_2}{\mathrm{[{\Omega}]}}\tag{5}
\end{eqnarray}
和分の積が使えるのは、2つの抵抗が並列接続されている時のみ
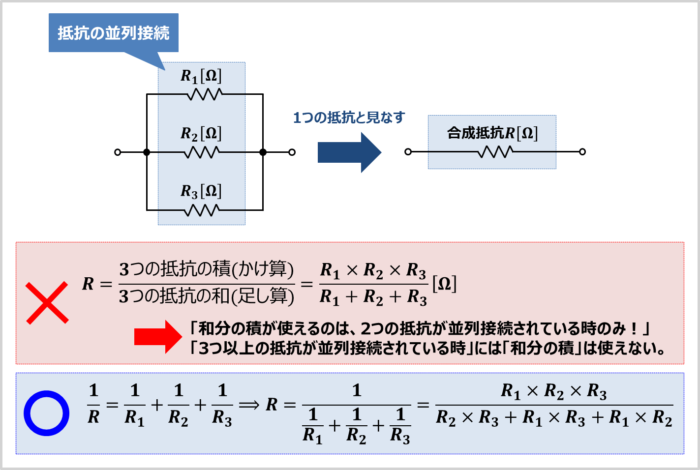

「和分の積が使えるのは、2つの抵抗が並列接続されている時のみ!」です。
「3つ以上の抵抗が並列接続されている時」には「和分の積」は使えません。
例えば、「\(R_1{\mathrm{[{\Omega}]}}\)の抵抗」と「\(R_2{\mathrm{[{\Omega}]}}\)の抵抗」と「\(R_3{\mathrm{[{\Omega}]}}\)の抵抗」が並列接続されている時、合成抵抗\(R{\mathrm{[{\Omega}]}}\)を
間違った計算式
\begin{eqnarray}
R=\frac{\mbox{3つの抵抗の積(かけ算)}}{\mbox{3つの抵抗の和(足し算)}}=\frac{R_1×R_2×R_3}{R_1+R_2+R_3}{\mathrm{[{\Omega}]}}\tag{6}
\end{eqnarray}
のように計算してはダメ!ということです。
「3つ以上の抵抗が並列接続されている時」に和分の積が使えない理由は、合成抵抗\(R{\mathrm{[{\Omega}]}}\)が複雑になるからです。
では実際に合成抵抗\(R{\mathrm{[{\Omega}]}}\)を計算してみましょう。
「\(R_1{\mathrm{[{\Omega}]}}\)の抵抗」と「\(R_2{\mathrm{[{\Omega}]}}\)の抵抗」と「\(R_3{\mathrm{[{\Omega}]}}\)の抵抗」が並列接続されている時、合成抵抗\(R\)の逆数\(\displaystyle\frac{1}{R}\)は各抵抗の逆数の和で計算することができ、次式で表されます。
\begin{eqnarray}
\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\tag{7}
\end{eqnarray}
上式を変形すると、合成抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表されます。
正しい計算式
\begin{eqnarray}
R&=&\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}}\\
\\
&=&\frac{R_1×R_2×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}\tag{8}
\end{eqnarray}
(6)式と(8)式は式が異なっており、(8)式の方が複雑ですよね。これが、「3つ以上の抵抗が並列接続されている時」には「和分の積」が使えない理由です。
ただし、和分の積を2回使えば、(6)式と等しくなります。
では実際に、和分の積を2回使って、合成抵抗\(R{\mathrm{[{\Omega}]}}\)を計算してみましょう。
「\(R_1{\mathrm{[{\Omega}]}}\)の抵抗」と「\(R_2{\mathrm{[{\Omega}]}}\)の抵抗」の合成抵抗\(R_{12}{\mathrm{[{\Omega}]}}\)は「和分の積」を用いると、次式で表されます。
\begin{eqnarray}
R_{12}=\frac{R_1×R_2}{R_1+R_2}{\mathrm{[{\Omega}]}}\tag{9}
\end{eqnarray}
次に、「\(R_{12}{\mathrm{[{\Omega}]}}\)の合成抵抗」と「\(R_3{\mathrm{[{\Omega}]}}\)の抵抗」の合成抵抗\(R{\mathrm{[{\Omega}]}}\)は「和分の積」を用いると、次式で表されます。
\begin{eqnarray}
R&=&\frac{R_{12}×R_3}{R_{12}+R_3}\\
\\
&=&\frac{\displaystyle\frac{R_1×R_2}{R_1+R_2}×R_3}{\displaystyle\frac{R_1×R_2}{R_1+R_2}+R_3}\\
\\
&=&\frac{R_1×R_2×R_3}{R_1×R_2+R_3(R_1+R_2)}\\
\\
&=&\frac{R_1×R_2×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}\tag{10}
\end{eqnarray}
(6)式と(10)式が等しくなりましたね。
和分の積は『コンデンサ』と『インダクタ』にも使用できる
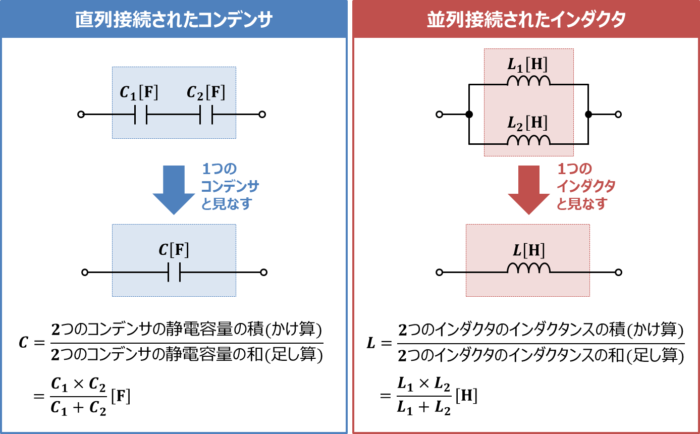

和分の積は、「並列接続された抵抗の合成抵抗値」を求める以外にも、
- 直列接続されたコンデンサの合成静電容量
- 並列接続されたインダクタの合成インダクタンス
を求める時にも使用することができます。
上図の左に「\(C_1{\mathrm{[F]}}\)のコンデンサ」と「\(C_2{\mathrm{[F]}}\)のコンデンサ」が直列接続されている図を示しています。この時、合成静電容量\(C{\mathrm{[F]}}\)は次式となります。
\begin{eqnarray}
C=\frac{\mbox{2つのコンデンサの静電容量の積(かけ算)}}{\mbox{2つのコンデンサの静電容量の和(足し算)}}=\frac{C_1×C_2}{C_1+C_2}{\mathrm{[F]}}\tag{11}
\end{eqnarray}
また、上図の右に「\(L_1{\mathrm{[H]}}\)のインダクタ」と「\(L_2{\mathrm{[H]}}\)のインダクタ」が並列接続されている図を示しています。この時、合成インダクタンス\(L{\mathrm{[H]}}\)は次式となります。
\begin{eqnarray}
L=\frac{\mbox{2つのインダクタのインダクタンスの積(かけ算)}}{\mbox{2つのインダクタのインダクタンスの和(足し算)}}=\frac{L_1×L_2}{L_1+L_2}{\mathrm{[H]}}\tag{12}
\end{eqnarray}
あわせて読みたい
直列接続されたコンデンサの合成静電容量の『求め方』と『例題』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-


【コンデンサの直列接続】静電容量の『計算』と『証明』について!
続きを見る
まとめ
この記事では、抵抗の『並列接続』と『和分の積』について、以下の内容を説明しました。
- 和分の積とは
- 和分の積の『証明』と『注意点』
- 和分の積は『抵抗』以外にも『コンデンサ』と『インダクタ』にも使用できること
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。