PFC回路(力率改善回路)の設計方法【詳細説明】

この記事ではPFC回路(力率改善回路)の設計方法を図を用いてかなり詳しく説明します。

PFC回路(力率改善回路)は動作モードとして、臨界モード(BCMモード)、電流連続モード(CCMモード)、電流不連続モード(DCMモード)があります。

一般的に200W程度までの小電力では臨界モード、200Wを超える大電力では電流連続モードで動作するように制御を行います。

まず、臨界モードの設計方法から詳しく説明します。電流連続モードの設計方法については、この記事の後半に記載しています。

PFC回路(力率改善回路)の設計方法(臨界モード/BCMモード)

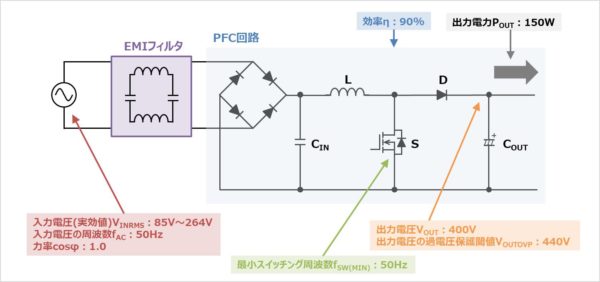
今回の設計条件を以下に示します。

上記の条件を用いてこれから臨界モードにおける力率改善回路(PFC回路)の設計を行うが、最小入力電圧(実効値)V_INRMS(MIN)時、MOSFETやインダクタに流れる電流が最大となり、その結果、電力損失も最大となります。そのため、設計においては最小入力電圧(実効値)V_INRMS(MIN)を用いて設計を行います。

電力の計算

PFC回路の設計にあたり、最初に入力電力P_INと皮相電力Sを導出する必要があります。

入力電力P_IN

入力電力P_INは、出力電力P_OUTと効率ηより以下の値となります。
\begin{eqnarray}
P_{IN}=\frac{P_{OUT}}{{\eta}}=166.666[W]
\end{eqnarray}

皮相電力S

皮相電力Sは、入力電力P_INと力率cosφより以下の値となります。
\begin{eqnarray}
S=\frac{P_{IN}}{cosφ}=\frac{P_{OUT}}{{\eta}・cosφ}=166.666[VA]
\end{eqnarray}

電流の計算

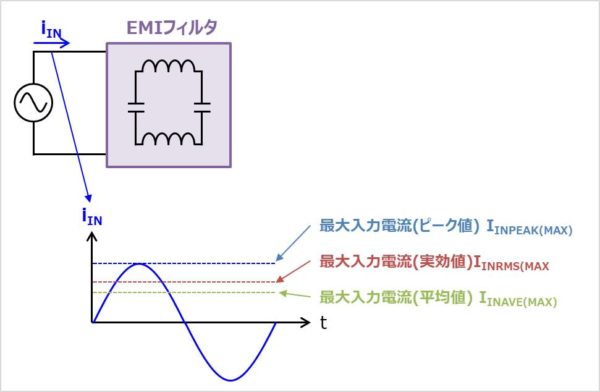
次に入力電流と出力電流を導出します。ここで求めた入力電流と出力電流はインダクタやMOSFETの設計の際に使用するパラメータです。

入力電流の導出

最大入力電流(実効値)I_INRMS(MAX)

最大入力電流(実効値)I_INRMS(MAX)は、皮相電力Sと最小入力電圧(実効値)V_INRMS(MIN)より、以下の値となります。
\begin{eqnarray}
I_{INRMS(MAX)}=\frac{S}{V_{INRMS(MIN)}}=\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=1.960[A]
\end{eqnarray}
通常は、上式のように力率cosφが分母に入ります。しかし、前提条件として力率cosφを”1”とすることで、力率cosφを省略している論文等もあります。

最大入力電流(ピーク値)I_INPEAK(MAX)

入力電流を正弦波と仮定すると、最大入力電流(ピーク値)I_INPEAK(MAX)は以下の値となります。
\begin{eqnarray}
I_{INPEAK(MAX)}=\sqrt{2}I_{INRMS(MAX)}= \sqrt{2}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=2.772[A]
\end{eqnarray}

最大入力電流(平均値)I_INAVE(MAX)

同様に、入力電流を正弦波と仮定すると、最大入力電流(平均値)I_INAVE(MAX)は以下の値となります。
\begin{eqnarray}
I_{INAVE(MAX)}=\frac{2}{{\pi}}I_{INPEAK(MAX)}=\displaystyle\frac{2\sqrt{2}}{{\pi}}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=1.765[A]
\end{eqnarray}
なお、正弦波の実行値と平均値の求め方については以下の記事に詳しく記載しています。

出力電流の導出

出力電流I_OUT

出力電流I_OUTは、出力電力P_OUTと出力電圧V_OUTから以下の値となります。
\begin{eqnarray}
I_{OUT}=\frac{P_{OUT}}{V_{OUT}}=0.375[A]
\end{eqnarray}

電圧の計算

次に入力電圧(ピーク値)を導出します。ここで求めた入力電圧(ピーク値)はインダクタやMOSFETの設計の際に使用するパラメータです。

最大入力電圧(ピーク値)V_INPEAK(MAX)

最大入力電圧(ピーク値)V_INPEAK(MAX)は以下の値となります。
\begin{eqnarray}
V_{INPEAK(MAX)}= \sqrt{2}V_{INRMS(MAX)}=373.352[V]
\end{eqnarray}

ブリッジダイオードの設計

ブリッジダイオードの設計では必要定格電圧・必要定格電流・消費電力(損失)を導出します。ここで求めた必要定格電圧と必要定格電流を満たすブリッジダイオードを選定します。

ブリッジダイオードの必要定格電圧の導出

最大ブリッジダイオード電圧V_BRIDGE(MAX)

最大ブリッジダイオード電圧V_BRIDGE(MAX)は最大入力電圧(ピーク値)V_INPEAK(MAX)と等しくなるため、以下の値となります。
\begin{eqnarray}
V_{BRIDGE(MAX)}= V_{INPEAK(MAX)}=373.352[V]
\end{eqnarray}
ここでディレーティングを80%とすると、ブリッジダイオードの必要定格電圧V_{BRIDGE(RATED)}は以下の値となります。
\begin{eqnarray}
V_{BRIDGE(RATED)}=\frac{V_{BRIDGE(MAX)}}{0.8}=466.690[V]
\end{eqnarray}

ブリッジダイオードの必要定格電流の導出

最大ブリッジダイオード電流(平均値)I_{BRIDGEAVE(MAX)}

最大ブリッジダイオード電流(平均値)I_{BRIDGEAVE(MAX)}は最大入力電流(平均値)I_INAVE(MAX)と等しくなるため、以下の値となります。
\begin{eqnarray}
I_{BRIDGEAVE(MAX)}=I_{INAVE(MAX)}=1.765[A]
\end{eqnarray}
ここでディレーティングを80%とすると、ブリッジダイオードの必要定格電流I_{BRIDGEAVE(RATED)}は以下の値となります。
\begin{eqnarray}
I_{BRIDGEAVE(RATED)}=\frac{ I_{BRIDGEAVE(MAX)}}{0.8}=2.207[A]
\end{eqnarray}

ブリッジダイオードの消費電力(損失)の導出

ブリッジダイオードの消費電力(損失)は主に順方向電圧V_Fによる導通損失となります。

ブリッジダイオードの導通損失P_BRIDGE

ブリッジダイオードの導通損失P_BRIDGEは「ブリッジダイオード内の2つのダイオードの順方向電圧V_Fと最大ブリッジダイオード電流(平均値)I_{BRIDGEAVE(MAX)}」から導出することができ、以下の値となります。ここでは順方向電圧V_Fを1.0[V]としています。
\begin{eqnarray}
P_{BRIDGE}= I_{BRIDGEAVE(MAX)}×2V_{F}=\frac{4\sqrt{2}}{{\pi}}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}} V_{F}=3.531[W]
\end{eqnarray}

インダクタの設計

インダクタの設計ではインダクタ電流・インダクタンスL・インダクタの導通損失を導出します。最大インダクタ電流(ピーク値)I_LPEAK(MAX)で飽和しないインダクタを選定します。

インダクタ電流の導出

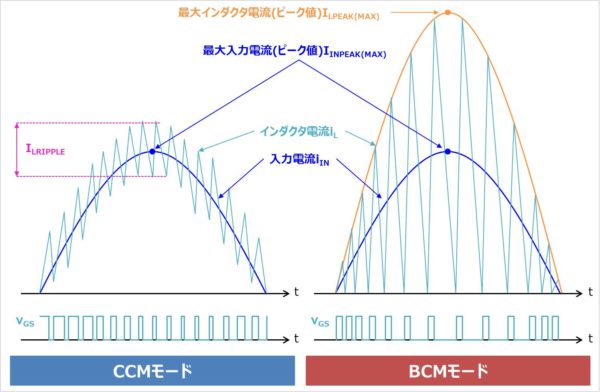
最大インダクタ電流(ピーク値)I_LPEAK(MAX)

インダクタLに流れる電流は、上図のように入力電流i_INにリプル電流が重畳します。ここで、上図より明らかですが、BCMモードの場合、最大インダクタ電流(ピーク値)I_LPEAK(MAX)は最大入力電流(ピーク値)I_INPEAK(MAX)の2倍となるため、以下の値となります。
\begin{eqnarray}
I_{LPEAK(MAX)}= 2I_{INPEAK(MAX)}=2\sqrt{2}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=5.546[A]
\end{eqnarray}

最大インダクタ電流(実効値)I_LRMS(MAX)

最大インダクタ電流(実効値)I_LRMS(MAX)は以下の値となります。
\begin{eqnarray}
I_{LRMS(MAX)}= \frac{I_{LPEAK(MAX)}}{\sqrt{6}}=\frac {2}{\sqrt{3}}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=2.264[A]
\end{eqnarray}

インダクタンスの導出

インダクタンスL

インダクタンスLは以下の値となります。インダクタンスLは最小入力電圧(実効値)V_INRMS(MIN)、最小スイッチング周波数f_SW(MIN)の条件で設計します。
\begin{eqnarray}
L{≥} \frac{{\eta}×{\cos}{\varphi}×{V_{INRMS(MIN)}}^2×(V_{OUT}-\sqrt{2} V_{INRMS(MIN)})}{2×P_{OUT}×V_{OUT}×f_{SW(MIN)}}=303.224[uH]
\end{eqnarray}
上式の導出は少し複雑ですので、この記事の最後の補足に導出方法を説明しています。

インダクタの導通損失の導出

ここで、選定したインダクタの直流抵抗R_Lを0.1Ωとすると、インダクタの導通損失P_Lは以下の値となります。
\begin{eqnarray}
P_{L}=R_{L}{ I_{LRMS(MAX)}}^2=0.513[W]
\end{eqnarray}

MOSFETの設計

MOSFETの設計では必要定格電圧・必要定格電流・消費電力(損失)を導出します。ここで求めた必要定格電圧と必要定格電流を満たすMOSFETを選定します。

MOSFETの必要定格電圧の導出

最大MOSFET電圧V_S(MAX)

最大MOSFET電圧V_S(MAX)は、出力電圧の過電圧保護閾値V_OUTOVPに出力ダイオードDの順方向電圧V_FDが加わった値となります。ここでは順方向電圧V_FDを1Vとします。
\begin{eqnarray}
V_{S(MAX)}= V_{OUTOVP}+V_{FD}=441.000[V]
\end{eqnarray}
ここでディレーティングを80%とすると、MOSFETの必要定格電圧V_S(RATED)は以下の値となります。
\begin{eqnarray}
V_{S(RATED)}=\frac{V_{S(MAX)}}{0.8}=551.250[V]
\end{eqnarray}

MOSFETの必要定格電流の導出

最大MOSFET電流(ピーク値)I_SPEAK(MAX)

最大MOSFET電流(ピーク値)I_SPEAK(MAX)は最大インダクタ電流(ピーク値)I_LPEAK(MAX)と等しいため以下の値となります。
\begin{eqnarray}
I_{SPEAK(MAX)}= I_{LPEAK(MAX)}=5.546[A]
\end{eqnarray}
ここでディレーティングを80%とすると、MOSFETの必要定格電流(ピーク値)I_SPEAK(RATED)は以下の値となります。
\begin{eqnarray}
I_{SPEAK(RATED)}=\frac{I_{SPEAK(MAX)}}{0.8}=6.932[A]
\end{eqnarray}

最大MOSFET電流(実効値)I_SRMS(MAX)

最大MOSFET電流(実効値)I_SRMS(MAX)は最大インダクタ電流(実効値)I_LRMS(MAX)を用いると以下の値となります。
\begin{eqnarray}
I_{SRMS (MAX)}&=&I_{LRMS (MAX)}×\sqrt{1-\displaystyle\frac{8\sqrt{2}×V_{INRMS(MIN)}}{3{\pi}V_{OUT}}}\\
&=& \frac {2}{\sqrt{3}}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}×\sqrt{1-\displaystyle\frac{8\sqrt{2}×V_{INRMS(MIN)}}{3{\pi}V_{OUT}}}\\
&=&1.954[A]
\end{eqnarray}
また最大インダクタ電流(ピーク値)I_LPEAK(MAX)を使用した下式でも同様の値となります。
\begin{eqnarray}
I_{SRMS (MAX)}&=&I_{LPEAK(MAX)}×\sqrt{\displaystyle\frac{1}{6}-\displaystyle\frac{4\sqrt{2}×V_{INRMS(MIN)}}{9{\pi}V_{OUT}}}\\
&=&2\sqrt{2}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}×\sqrt{\displaystyle\frac{1}{6}-\displaystyle\frac{4\sqrt{2}×V_{INRMS(MIN)}}{9{\pi}V_{OUT}}}\\
&=&1.954[A]
\end{eqnarray}
ここでディレーティングを80%とすると、MOSFETの必要定格電流(実効値)I_SRMS(RATED)は以下の値となります。
\begin{eqnarray}
I_{SRMS(RATED)}=\frac{I_{SRMS(MAX)}}{0.8}=2.443[A]
\end{eqnarray}

MOSFETの消費電力(損失)の導出

MOSFETの消費電力(損失)には導通損失、スイッチング損失、ディスチャージ損失があります。ここで、選定したMOSFETのパラメータが下記だと仮定して、損失計算を行います。下記のデータはMOSFETのデータシートに記載されているので、選定したMOSFETによって変えてください。

• オン抵抗R_ON：0.8Ω
• 立ち上がり時間T_R：10ns
• 立ち下がり時間T_F：10ns
• 出力容量C_OSS：100pF

MOSFETの導通損失P_SCOND

最大MOSFET電流(実効値)I_SRMS(MAX)とオン抵抗R_ONより、導通損失P_SCONDは以下の値となります。
\begin{eqnarray}
P_{SCOND}=R_{ON}{I_{SRMS(MAX)}}^2=3.055[W]
\end{eqnarray}

MOSFETのスイッチング損失P_SSW

BCMモードの場合、MOSFETのターンオン時は流れている電流が0Aなので、ターンオン損失は無視できます。したがって、スイッチング損失はターンオフ損失のみを考慮します。また、常に最大MOSFET電流(ピーク値)I_SPEAK(MAX)でターンオフするわけではないため、最大MOSFET電流(ピーク値)I_SPEAK(MAX)の平均化を行います。ターンオフ点をプロットすると、正弦波となっており、そのピーク値は入力電流の2倍となります。したがって、ターンオフ点をプロットすることにより作成された正弦波の平均値I_SOFFAVEは以下の値となります。
\begin{eqnarray}
I_{SOFFAVE}=2I_{INAVE(MAX)}=3.531[A]
\end{eqnarray}
また、BCMモードでは入力電圧の大きさにより、スイッチング周波数が常に変化しています。そのため、スイッチング損失を導出する際には最小スイッチング周波数f_SW(MIN)ではなく、平均スイッチング周波数f_SW(AVE)を使用します。平均スイッチング周波数f_SW(AVE)は厳密には求めることが困難のため、ここでは最小スイッチング周波数f_SW(MIN)を1.2倍した値を平均スイッチング周波数f_SW(AVE)と定義します。
\begin{eqnarray}
f_{SW(AVE)}=1.2×f_{SW(MIN)}=60[kHz]
\end{eqnarray}
以上より、MOSFETのスイッチング損失P_SSWは以下の値となります。
\begin{eqnarray}
P_{SSW}=\frac{1}{6}V_{OUT} I_{SOFFAVE}×T_{F}×f_{SW(AVE)}=0.141[W]
\end{eqnarray}
上式のスイッチング損失の導出方法は以下の記事に記載しています。

MOSFETのディスチャージ損失P_SCOSS

MOSFETのターンオン時において、出力容量C_OSSに蓄積された電荷が放電することでディスチャージ損失P_SCOSSが発生します。このディスチャージ損失P_SCOSSは以下の値となります。
\begin{eqnarray}
P_{SCOSS}=\frac{1}{2}C_{OSS}{V_{OUT}}^2 f_{SW(AVE)}=0.480[W]
\end{eqnarray}

以上をまとめると、MOSFETの合計損失P_Sは以下の値となります。
\begin{eqnarray}
P_{S}=P_{SCOND}+ P_{SSW}+ P_{SCOSS}=3.676[W]
\end{eqnarray}

ダイオードの設計

ダイオードの設計では必要定格電圧・必要定格電流・消費電力(損失)を導出します。ここで求めた必要定格電圧と必要定格電流を満たすダイオードを選定します。

ダイオードの必要定格電圧の導出

最大ダイオード電圧V_D(MAX)

MOSFETのオン時、ダイオードには出力電圧V_OUTが印加されます。そのため、出力電圧の過電圧保護閾値V_OUTOVPを用いると、最大ダイオード電圧V_D(MAX)は以下の値となります。
\begin{eqnarray}
V_{D(MAX)}=V_{OUTOVP}=440.000[V]
\end{eqnarray}
ここでディレーティングを80%とすると、ダイオードの必要定格電圧V_D(RATED)は以下の値となります。
\begin{eqnarray}
V_{D(RATED)}=\frac{V_{D(MAX)}}{0.8}=550.000[V]
\end{eqnarray}

ダイオードの必要定格電流の導出

最大ダイオード電流(ピーク値)I_DPEAK(MAX)

最大ダイオード電流(ピーク値) I_DPEAK(MAX)は最大インダクタ電流(ピーク値)I_LPEAK(MAX)と等しいため以下の値となります。
\begin{eqnarray}
I_{DPEAK(MAX)}= I_{LPEAK(MAX)}=5.546[A]
\end{eqnarray}
ここでディレーティングを80%とすると、ダイオードの必要定格電流(ピーク値)I_DPEAK(RATED)は以下の値となります。
\begin{eqnarray}
I_{DPEAK(RATED)}=\frac{I_{DPEAK(MAX)}}{0.8}=6.932[A]
\end{eqnarray}

最大ダイオード電流(平均値)I_DAVE(MAX)

出力コンデンサC_OUTに流れる電流の平均値は0Aとなります。そのため、最大ダイオード電流(平均値)I_DAVE(MAX)は出力電流I_OUTと等しくなります。
\begin{eqnarray}
I_{DAVE(MAX)}= I_{OUT}=0.375[A]
\end{eqnarray}
ここでディレーティングを80%とすると、ダイオードの必要定格電流(平均値)I_DAVE(RATED)は以下の値となります。
\begin{eqnarray}
I_{DAVE(RATED)}=\frac{I_{DAVE(MAX)}}{0.8}=0.496[A]
\end{eqnarray}

ダイオードの消費電力(損失)の導出

ダイオードの消費電力(損失)は主に順方向電圧V_FDによる導通損失となります。

ダイオードの導通損失P_DCOND

ダイオードの導通損失P_DCONDは以下の値となります。ここでは順方向電圧V_FDを1.0[V]としています。
\begin{eqnarray}
P_{DCOND}= I_{DAVE(MAX)}V_{FD}=0.375[W]
\end{eqnarray}

出力コンデンサの設計

出力コンデンサの設計では容量を導出します。また、補足として出力コンデンサに流れる電流も導出しています。

出力コンデンサの容量の導出

出力コンデンサC_OUTの容量はこれから説明する「出力電圧リプル」と「保持時間」で求めた容量のうち、大きい容量にディレーティングを考慮して選定します。

出力電圧リプルV_OUTRIPPLE

出力電圧リプルV_OUTRIPPLEは以下の式で導出することができます。
\begin{eqnarray}
V_{OUTRIPPLE}=\frac{I_{OUT}}{2{\pi}f_{AC}C_{OUT}}=\frac{P_{OUT}}{2{\pi}f_{AC}C_{OUT}V_{OUT}}
\end{eqnarray}
上式の導出方法はこの記事の最後に記載しています。

以上より、出力電圧リプルV_OUTRIPPLEによる出力コンデンサC_OUTの条件は以下の値となります。
\begin{eqnarray}
C_{OUT}{≥}\frac{I_{OUT}}{2{\pi}f_{AC} V_{OUTRIPPLE}}=119.366[uF]
\end{eqnarray}

保持時間T_HOLD

入力が遮断されると、出力電圧V_OUTが低下します。ここで、出力電圧がV_OUT(MIN)になる時間を保持時間T_HOLDとすると、保持時間T_HOLDは以下の式で導出することができます。
\begin{eqnarray}
T_{HOLD}=\frac{C_{OUT}({V_{OUT}}^2-{V_{OUT(MIN)}}^2)}{2P_{OUT}}
\end{eqnarray}
上式の導出方法と保持時間については以下の記事に詳しく記載しています。

以上より、保持時間T_HOLDによる出力コンデンサC_OUTの条件は以下の値となります。
\begin{eqnarray}
C_{OUT}{≥}\frac{2P_{OUT}T_{HOLD}}{{V_{OUT}}^2-{V_{OUT(MIN)}}^2}=85.714[uF]
\end{eqnarray}

コンデンサには誤差(±20%程度)があるため、最悪条件においても上記の条件を満たせるようにディレーティングを考慮します。上記で求めた出力コンデンサC_OUTの条件において、ディレーティングを80%とすると、出力コンデンサの必要容量C_OUT1は以下の値となります。
\begin{eqnarray}
C_{OUT1}=\frac{C_{OUT}}{0.8}=149.208[uF]
\end{eqnarray}

出力コンデンサに流れる電流の導出

最大出力コンデンサ電流(実効値)I_COUTRMS(MAX)

最大出力コンデンサ電流(実効値)I_COUTRMS(MAX)は以下の値となります。
\begin{eqnarray}
I_{COUTRMS(MAX)}= \sqrt{\displaystyle\frac{32\sqrt{2}×{P_{OUT}}^2}{9{\pi} V_{INRMS(MIN)}V_{OUT}}-\left(\displaystyle\frac{ P_{OUT}}{ V_{OUT}}\right)^2}=0.958[A]
\end{eqnarray}
出力コンデンサに流れる電流と出力コンデンサの等価直列抵抗(ESR)によっても電圧変動は生じますが、出力電圧が大きく出力電流が小さいため、この電圧変動は無視することができます。しかし、この最大出力コンデンサ電流(実効値)I_COUTRMS(MAX)は出力コンデンサの電力損失に影響を与えます。

入力コンデンサの設計

入力コンデンサの設計では必要定格電圧と容量を導出します。ここで求めた必要定格電圧を満たす入力コンデンサを選定します。
なお、入力コンデンサはインダクタに流れる高周波リプル電流とMOSFETのオン/オフによって生じるスイッチングノイズをフィルタするために接続されています。また入力コンデンサにはフィルムコンデンサを使用します。

入力コンデンサの必要定格電圧の導出

最大入力コンデンサ電圧V_CIN(MAX)

ブリッジダイオードの順方向電圧V_Fを無視すると、最大入力コンデンサ電圧V_CIN(MAX)は最大入力電圧(ピーク値)V_INPEAK(MAX)と等しくなるため以下の値となります。
\begin{eqnarray}
V_{CIN(MAX)}=V_{INPEAK(MAX)}=373.352[V]
\end{eqnarray}
ここでディレーティングを80%とすると、入力コンデンサの必要定格電圧V_CIN(RATED)は以下の値となります。
\begin{eqnarray}
V_{CIN(RATED)}=\frac{V_{CIN(MAX)}}{0.8}=466.690[V]
\end{eqnarray}

入力コンデンサの容量の導出

入力コンデンサの容量の導出方法には2つの設計方法があります。

設計方法１

設計方法1では、最大入力電流(実効値)I_INRMS(MAX)と最小入力電圧(実効値)V_INRMS(MIN)を用いた設計です。まず、最小入力電圧(実効値)V_INRMS(MIN)のリプル率rを決めます。リプル率rは一般的には1%～10%の間に設定します。ここではrを10%(0.1)として設計をします。この場合、入力コンデンサの容量は以下の値となります。
\begin{eqnarray}
C_{IN}=2×\frac{I_{INRMS(MAX)}}{2{\pi}f_{SW(MIN)}rV_{INRMS(MIN)}}=1.469[uF]
\end{eqnarray}

設計方法２

設計方法2では、まずインダクタリプル電流I_LRIPPLEと入力コンデンサ電圧のリプル電圧V_CINRIPPLEを用いた設計です。
インダクタリプル電流I_LRIPPLEは以下の式で求めることができます。
\begin{eqnarray}
I_{LRIPPLE}=2×I_{INPEAK(MAX)}
\end{eqnarray}
また、入力コンデンサ電圧のリプル電圧V_CINRIPPLEは以下の式で求めることができます(ブリッジダイオードの順方向電圧は入力コンデンサ電圧に比べて十分小さいため省略しています)。リプル率rは一般的には1%～10%の間に設定します。ここではrを10%(0.1)として設計をします。
\begin{eqnarray}
V_{CINRIPPLE}=r×V_{INPEAK(MIN)}
\end{eqnarray}
上式のインダクタリプル電流I_LRIPPLEと入力コンデンサ電圧のリプル電圧V_CINRIPPLEを用いると、入力コンデンサの容量は以下の値となります。
\begin{eqnarray}
C_{IN}=\frac{I_{LRIPPLE}}{8f_{SW(MIN)}V_{CINRIPPLE}}=1.153[uF]
\end{eqnarray}

上記の設計で求めた入力コンデンサC_INの容量に近い値を選定します。この時、入力コンデンサC_INの容量が大きいほど、EMIフィルタを小さくすることができますが、電流歪みが発生するため、力率が低下します(特に高入力電圧＆高負荷時に力率が低下します)。

PFC回路(力率改善回路)の設計方法(電流連続モード/CCMモード)

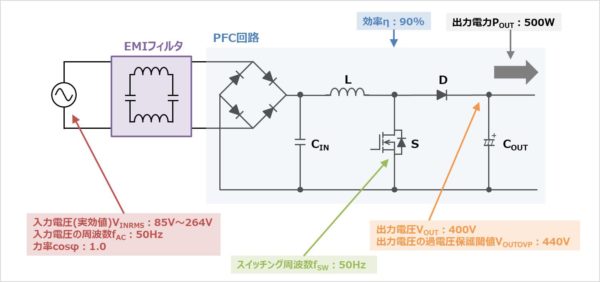
今回の設計条件を以下に示します。

上記の条件を用いてこれから臨界モードにおける力率改善回路(PFC回路)の設計を行うが、最小入力電圧(実効値)V_INRMS(MIN)時、MOSFETやインダクタに流れる電流が最大となり、その結果、電力損失も最大となります。そのため、設計においては最小入力電圧(実効値)V_INRMS(MIN)を用いて設計を行います。

電力の計算

PFC回路の設計にあたり、最初に入力電力P_INと皮相電力Sを導出する必要があります。

入力電力P_IN

入力電力P_INは、出力電力P_OUTと効率ηより以下の値となります。
\begin{eqnarray}
P_{IN}=\frac{P_{OUT}}{{\eta}}=555.556[W]
\end{eqnarray}

皮相電力S

皮相電力Sは、入力電力P_INと力率cosφより以下の値となります。
\begin{eqnarray}
S=\frac{P_{IN}}{cosφ}=\frac{P_{OUT}}{{\eta}・cosφ}=555.556[VA]
\end{eqnarray}

電流の計算

次に入力電流と出力電流を導出します。ここで求めた入力電流と出力電流はインダクタやMOSFETの設計の際に使用するパラメータです。

入力電流の導出

最大入力電流(実効値)I_INRMS(MAX)

最大入力電流(実効値)I_INRMS(MAX)は、皮相電力Sと最小入力電圧(実効値)V_INRMS(MIN)より、以下の値となります。
\begin{eqnarray}
I_{INRMS(MAX)}=\frac{S}{V_{INRMS(MIN)}}=\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=6.536[A]
\end{eqnarray}
通常は、上式のように力率cosφが分母に入ります。しかし、前提条件として力率cosφを”1”とすることで、力率cosφを省略している論文等もあります。

最大入力電流(ピーク値)I_INPEAK(MAX)

入力電流を正弦波と仮定すると、最大入力電流(ピーク値)I_INPEAK(MAX)は以下の値となります。
\begin{eqnarray}
I_{INPEAK(MAX)}=\sqrt{2}I_{INRMS(MAX)}= \sqrt{2}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=9.243 [A]
\end{eqnarray}

最大入力電流(平均値)I_INAVE(MAX)

同様に、入力電流を正弦波と仮定すると、最大入力電流(平均値)I_INAVE(MAX)は以下の値となります。
\begin{eqnarray}
I_{INAVE(MAX)}=\frac{2}{{\pi}}I_{INPEAK(MAX)}=\displaystyle\frac{2\sqrt{2}}{{\pi}}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=5.884[A]
\end{eqnarray}
なお、正弦波の実行値と平均値の求め方については以下の記事に詳しく記載しています。

出力電流の導出

出力電流I_OUT

出力電流I_OUTは、出力電力P_OUTと出力電圧V_OUTから以下の値となります。
\begin{eqnarray}
I_{OUT}=\frac{P_{OUT}}{V_{OUT}}=1.250[A]
\end{eqnarray}

電圧の計算

次に入力電圧(ピーク値)を導出します。ここで求めた入力電圧(ピーク値)はインダクタやMOSFETの設計の際に使用するパラメータです。

最大入力電圧(ピーク値)V_INPEAK(MAX)

最大入力電圧(ピーク値)V_INPEAK(MAX)は以下の値となります。
\begin{eqnarray}
V_{INPEAK(MAX)}= \sqrt{2}V_{INRMS(MAX)}=373.352[V]
\end{eqnarray}

ブリッジダイオードの設計

ブリッジダイオードの設計では必要定格電圧・必要定格電流・消費電力(損失)を導出します。ここで求めた必要定格電圧と必要定格電流を満たすブリッジダイオードを選定します。

ブリッジダイオードの必要定格電圧の導出

最大ブリッジダイオード電圧V_BRIDGE(MAX)

最大ブリッジダイオード電圧V_BRIDGE(MAX)は最大入力電圧(ピーク値)V_INPEAK(MAX)と等しくなるため、以下の値となります。
\begin{eqnarray}
V_{BRIDGE(MAX)}= V_{INPEAK(MAX)}=373.352[V]
\end{eqnarray}
ここでディレーティングを80%とすると、ブリッジダイオードの必要定格電圧V_{BRIDGE(RATED)}は以下の値となります。
\begin{eqnarray}
V_{BRIDGE(RATED)}=\frac{V_{BRIDGE(MAX)}}{0.8}=466.690[V]
\end{eqnarray}

ブリッジダイオードの必要定格電流の導出

最大ブリッジダイオード電流(平均値)I_{BRIDGEAVE(MAX)}

最大ブリッジダイオード電流(平均値)I_{BRIDGEAVE(MAX)}は最大入力電流(平均値)I_INAVE(MAX)と等しくなるため、以下の値となります。
\begin{eqnarray}
I_{BRIDGEAVE(MAX)}=I_{INAVE(MAX)}=5.884[A]
\end{eqnarray}
ここでディレーティングを80%とすると、ブリッジダイオードの必要定格電流I_{BRIDGEAVE(RATED)}は以下の値となります。
\begin{eqnarray}
I_{BRIDGEAVE(RATED)}=\frac{ I_{BRIDGEAVE(MAX)}}{0.8}=7.356[A]
\end{eqnarray}

ブリッジダイオードの消費電力(損失)の導出

ブリッジダイオードの消費電力(損失)は主に順方向電圧V_Fによる導通損失となります。

ブリッジダイオードの導通損失P_BRIDGE

ブリッジダイオードの導通損失P_BRIDGEは「ブリッジダイオード内の2つのダイオードの順方向電圧V_Fと最大ブリッジダイオード電流(平均値)I_{BRIDGEAVE(MAX)}」から導出することができ、以下の値となります。ここでは順方向電圧V_Fを1.0[V]としています。
\begin{eqnarray}
P_{BRIDGE}= I_{BRIDGEAVE(MAX)}×2V_{F}=\frac{4\sqrt{2}}{{\pi}}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}} V_{F}=11.769[W]
\end{eqnarray}

インダクタの設計

インダクタの設計ではインダクタ電流・インダクタンスL・インダクタの導通損失を導出します。最大インダクタ電流(ピーク値)I_LPEAK(MAX)で飽和しないインダクタを選定します。

インダクタ電流の導出

最大インダクタ電流(ピーク値)I_LPEAK(MAX)

CCMモードの場合はまず、インダクタリプル電流を求めます。入力電流i_INに対するリプル電流の割合を%RIPPLEとすると、インダクタリプル電流I_LRIPPLEは以下の値となります。ここでは、入力電流i_INに対するリプル電流の割合%RIPPLEを30%(0.3)として設計をしています。
\begin{eqnarray}
I_{LRIPPLE}= I_{INPEAK(MAX)}×{\%}RIPPLE=2.773[A]
\end{eqnarray}
したがって、最大インダクタ電流(ピーク値)I_LPEAK(MAX)は以下の値となります。
\begin{eqnarray}
I_{LPEAK(MAX)}&=&I_{INPEAK(MAX)}+\frac{1}{2}I_{LRIPPLE}\\
&=&\sqrt{2}\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}\left(1+\frac{{\%}RIPPLE}{2}\right)=10.630[A]
\end{eqnarray}
上式において、%RIPPLEに2を代入すると、BCMモードの時と同じ式となります。ここで、リプル電流の割合%RIPPLEの目安は、インダクタのサイズを考慮して一般的に15%～40%程度が最適となります。リプル電流が小さい場合、ゼロクロス付近でのひずみの低減、出力コンデンサと入力コンデンサに流れるリプル電流の低減、MOSFETとダイオードに流れるピーク電流の低減とメリットが多いですが、インダクタが大型化します。また、ピーク電流で飽和しないようにコアの選定により一層注意が必要になります。

最大インダクタ電流(実効値)I_LRMS(MAX)

インダクタリプル電流I_LRIPPLEを無視すると、最大インダクタ電流(実効値)I_LRMS(MAX)は最大入力電流(実効値) I_INRMS(MAX)と等しくなります。したがって、最大インダクタ電流(実効値)I_LRMS(MAX)は以下の値となります。
\begin{eqnarray}
I_{LRMS(MAX)}= I_{INRMS(MAX)}= \frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}=6.536[A]
\end{eqnarray}

インダクタンスの導出

インダクタンスL

インダクタンスLは以下の値となります。インダクタンスLは最小入力電圧(実効値)V_INRMS(MIN)、最小スイッチング周波数f_SW(MIN)の条件で設計します。
\begin{eqnarray}
L{≥} \frac{{\eta}×{\cos}{\varphi}×{V_{INRMS(MIN)}}^2×(V_{OUT}-\sqrt{2} V_{INRMS(MIN)})}{{\%}RIPPLE×P_{OUT}×V_{OUT}×f_{SW}}=606.449[uH]
\end{eqnarray}
上式の導出は少し複雑ですので、この記事の最後の補足に導出方法を説明しています。導出はBCMモードにおいて行っていますが、考え方はCCMモードでも同じです。

インダクタの導通損失の導出

ここで、選定したインダクタの直流抵抗R_Lを0.1Ωとすると、インダクタの導通損失P_Lは以下の値となります。
\begin{eqnarray}
P_{L}=R_{L}{ I_{LRMS(MAX)}}^2=4.272[W]
\end{eqnarray}

MOSFETの設計

MOSFETの設計では必要定格電圧・必要定格電流・消費電力(損失)を導出します。ここで求めた必要定格電圧と必要定格電流を満たすMOSFETを選定します。

MOSFETの必要定格電圧の導出

最大MOSFET電圧V_S(MAX)

最大MOSFET電圧V_S(MAX)は、出力電圧の過電圧保護閾値V_OUTOVPに出力ダイオードDの順方向電圧V_FDが加わった値となります。ここでは順方向電圧V_FDを1Vとします。
\begin{eqnarray}
V_{S(MAX)}= V_{OUTOVP}+V_{FD}=441.000[V]
\end{eqnarray}
ここでディレーティングを80%とすると、MOSFETの必要定格電圧V_S(RATED)は以下の値となります。
\begin{eqnarray}
V_{S(RATED)}=\frac{V_{S(MAX)}}{0.8}=551.250[V]
\end{eqnarray}

MOSFETの必要定格電流の導出

最大MOSFET電流(ピーク値)I_SPEAK(MAX)

最大MOSFET電流(ピーク値)I_SPEAK(MAX)は最大インダクタ電流(ピーク値)I_LPEAK(MAX)と等しいため以下の値となります。
\begin{eqnarray}
I_{SPEAK(MAX)}= I_{LPEAK(MAX)}=10.630 [A]
\end{eqnarray}
ここでディレーティングを80%とすると、MOSFETの必要定格電流(ピーク値)I_SPEAK(RATED)は以下の値となります。
\begin{eqnarray}
I_{SPEAK(RATED)}=\frac{I_{SPEAK(MAX)}}{0.8}=13.287 [A]
\end{eqnarray}

最大MOSFET電流(実効値)I_SRMS(MAX)

最大MOSFET電流(実効値)I_SRMS(MAX)は最大インダクタ電流(実効値)I_LRMS(MAX)を用いると以下の値となります。
\begin{eqnarray}
I_{SRMS (MAX)}&=&I_{LRMS (MAX)}×\sqrt{1-\displaystyle\frac{8\sqrt{2}×V_{INRMS(MIN)}}{3{\pi}V_{OUT}}}\\
&=&\frac{P_{OUT}}{{\eta}・cosφ・V_{INRMS(MIN)}}×\sqrt{1-\displaystyle\frac{8\sqrt{2}×V_{INRMS(MIN)}}{3{\pi}V_{OUT}}}\\
&=&5.641[A]
\end{eqnarray}
ここでディレーティングを80%とすると、MOSFETの必要定格電流(実効値)I_SRMS(RATED)は以下の値となります。
\begin{eqnarray}
I_{SRMS(RATED)}=\frac{I_{SRMS(MAX)}}{0.8}=7.651[A]
\end{eqnarray}

MOSFETの消費電力(損失)の導出

MOSFETの消費電力(損失)には導通損失、スイッチング損失、ディスチャージ損失があります。ここで、選定したMOSFETのパラメータが下記だと仮定して、損失計算を行います。下記のデータはMOSFETのデータシートに記載されているので、選定したMOSFETによって変えてください。

• オン抵抗R_ON：0.8Ω
• 立ち上がり時間T_R：10ns
• 立ち下がり時間T_F：10ns
• 出力容量C_OSS：100pF

MOSFETの導通損失P_SCOND

最大MOSFET電流(実効値)I_SRMS(MAX)とオン抵抗R_ONより、導通損失P_SCONDは以下の値となります。
\begin{eqnarray}
P_{SCOND}=R_{ON}{I_{SRMS(MAX)}}^2=25.457[W]
\end{eqnarray}

MOSFETのスイッチング損失P_SSW

CCMモードでは、MOSFETのターンオンとターンオフの中間点の箇所をプロットすると、正弦波となっており、そのピーク値は入力電流と等しくなります。そのため、MOSFETのターンオンとターンオフの中間点の箇所をプロットすることにより作成された正弦波の平均値I_SAVEは以下の値となります。
\begin{eqnarray}
I_{SAVE}=I_{INAVE(MAX)}=5.884[A]
\end{eqnarray}
以上より、MOSFETのスイッチング損失P_SSWは以下の値となります。
\begin{eqnarray}
P_{SSW}=\frac{1}{6}V_{OUT} I_{SAVE}×(T_{F}+T_{R})×f_{SW}=0.785[W]
\end{eqnarray}
上式のスイッチング損失の導出方法は以下の記事に記載しています。

MOSFETのディスチャージ損失P_SCOSS

MOSFETのターンオン時において、出力容量C_OSSに蓄積された電荷が放電することでディスチャージ損失P_SCOSSが発生します。このディスチャージ損失P_SCOSSは以下の値となります。
\begin{eqnarray}
P_{SCOSS}=\frac{1}{2}C_{OSS}{V_{OUT}}^2 f_{SW}=0.400[W]
\end{eqnarray}

以上をまとめると、MOSFETの合計損失P_Sは以下の値となります。
\begin{eqnarray}
P_{S}=P_{SCOND}+ P_{SSW}+ P_{SCOSS}=26.642[W]
\end{eqnarray}

ダイオードの設計

ダイオードの設計では必要定格電圧・必要定格電流・消費電力(損失)を導出します。ここで求めた必要定格電圧と必要定格電流を満たすダイオードを選定します。

ダイオードの必要定格電圧の導出

最大ダイオード電圧V_D(MAX)

MOSFETのオン時、ダイオードには出力電圧V_OUTが印加されます。そのため、出力電圧の過電圧保護閾値V_OUTOVPを用いると、最大ダイオード電圧V_D(MAX)は以下の値となります。
\begin{eqnarray}
V_{D(MAX)}=V_{OUTOVP}=440.000[V]
\end{eqnarray}
ここでディレーティングを80%とすると、ダイオードの必要定格電圧V_D(RATED)は以下の値となります。
\begin{eqnarray}
V_{D(RATED)}=\frac{V_{D(MAX)}}{0.8}=550.000[V]
\end{eqnarray}

ダイオードの必要定格電流の導出

最大ダイオード電流(ピーク値)I_DPEAK(MAX)

最大ダイオード電流(ピーク値)I_DPEAK(MAX)は最大インダクタ電流(ピーク値)I_LPEAK(MAX)と等しいため以下の値となります。
\begin{eqnarray}
I_{DPEAK(MAX)}= I_{LPEAK(MAX)}=10.630[A]
\end{eqnarray}
ここでディレーティングを80%とすると、ダイオードの必要定格電流(ピーク値)I_DPEAK(RATED)は以下の値となります。
\begin{eqnarray}
I_{DPEAK(RATED)}=\frac{I_{DPEAK(MAX)}}{0.8}=13.287[A]
\end{eqnarray}

最大ダイオード電流(平均値)I_DAVE(MAX)

出力コンデンサC_OUTに流れる電流の平均値は0Aとなります。そのため、最大ダイオード電流(平均値) I_DAVE(MAX)は出力電流I_OUTと等しくなります。
\begin{eqnarray}
I_{DAVE(MAX)}= I_{OUT}=1.250[A]
\end{eqnarray}
ここでディレーティングを80%とすると、ダイオードの必要定格電流(平均値)I_DAVE(RATED)は以下の値となります。
\begin{eqnarray}
I_{DAVE(RATED)}=\frac{I_{DAVE(MAX)}}{0.8}=1.563[A]
\end{eqnarray}

ダイオードの消費電力(損失)の導出

ダイオードの消費電力(損失)は主に順方向電圧V_FDによる導通損失となります。

ダイオードの導通損失P_DCOND

ダイオードの導通損失P_DCONDは以下の値となります。ここでは順方向電圧V_FDを1.0[V]としています。
\begin{eqnarray}
P_{DCOND}= I_{DAVE(MAX)}V_{FD}=1.250[W]
\end{eqnarray}

出力コンデンサの設計

出力コンデンサの設計では容量を導出します。また、補足として出力コンデンサに流れる電流も導出しています。

出力コンデンサの容量の導出

出力コンデンサC_OUTの容量はこれから説明する「出力電圧リプル」と「保持時間」で求めた容量のうち、大きい容量にディレーティングを考慮して選定します。

出力電圧リプルV_OUTRIPPLE

出力電圧リプルV_OUTRIPPLEは以下の式で導出することができます。
\begin{eqnarray}
V_{OUTRIPPLE}=\frac{I_{OUT}}{2{\pi}f_{AC}C_{OUT}}=\frac{P_{OUT}}{2{\pi}f_{AC}C_{OUT}V_{OUT}}
\end{eqnarray}
上式の導出方法はこの記事の最後に記載しています。

以上より、出力電圧リプルV_OUTRIPPLEによる出力コンデンサC_OUTの条件は以下の値となります。
\begin{eqnarray}
C_{OUT}{≥}\frac{I_{OUT}}{2{\pi}f_{AC} V_{OUTRIPPLE}}=397.887[uF]
\end{eqnarray}

保持時間T_HOLD

入力が遮断されると、出力電圧V_OUTが低下します。ここで、出力電圧がV_OUT(MIN)になる時間を保持時間T_HOLDとすると、保持時間T_HOLDは以下の式で導出することができます。
\begin{eqnarray}
T_{HOLD}=\frac{C_{OUT}({V_{OUT}}^2-{V_{OUT(MIN)}}^2)}{2P_{OUT}}
\end{eqnarray}
上式の導出方法と保持時間については以下の記事に詳しく記載しています。

以上より、保持時間T_HOLDによる出力コンデンサC_OUTの条件は以下の値となります。
\begin{eqnarray}
C_{OUT}{≥}\frac{2P_{OUT}T_{HOLD}}{{V_{OUT}}^2-{V_{OUT(MIN)}}^2}=285.714[uF]
\end{eqnarray}

コンデンサには誤差(±20%程度)があるため、最悪条件においても上記の条件を満たせるようにディレーティングを考慮します。上記で求めた出力コンデンサC_OUTの条件において、ディレーティングを80%とすると、出力コンデンサの必要容量C_OUT1は以下の値となります。
\begin{eqnarray}
C_{OUT1}=\frac{C_{OUT}}{0.8}=497.359 [uF]
\end{eqnarray}

出力コンデンサに流れる電流の導出

最大出力コンデンサ電流(実効値)I_COUTRMS(MAX)

最大出力コンデンサ電流(実効値)I_COUTRMS(MAX)は以下の値となります。
\begin{eqnarray}
I_{COUTRMS(MAX)}= \sqrt{\displaystyle\frac{8\sqrt{2}×{P_{OUT}}^2}{3{\pi} V_{INRMS(MIN)}V_{OUT}}-\left(\displaystyle\frac{ P_{OUT}}{ V_{OUT}}\right)^2}=2.695[A]
\end{eqnarray}
出力コンデンサに流れる電流と出力コンデンサの等価直列抵抗(ESR)によっても電圧変動は生じますが、出力電圧が大きく出力電流が小さいため、この電圧変動は無視することができます。しかし、この最大出力コンデンサ電流(実効値)I_COUTRMS(MAX)は出力コンデンサの電力損失に影響を与えます。

入力コンデンサの設計

入力コンデンサの設計では必要定格電圧と容量を導出します。ここで求めた必要定格電圧を満たす入力コンデンサを選定します。
なお、入力コンデンサはインダクタに流れる高周波リプル電流とMOSFETのオン/オフによって生じるスイッチングノイズをフィルタするために接続されています。また入力コンデンサにはフィルムコンデンサを使用します。

入力コンデンサの必要定格電圧の導出

最大入力コンデンサ電圧V_CIN(MAX)

ブリッジダイオードの順方向電圧V_Fを無視すると、最大入力コンデンサ電圧V_CIN(MAX)は最大入力電圧(ピーク値)V_INPEAK(MAX)と等しくなるため以下の値となります。
\begin{eqnarray}
V_{CIN(MAX)}=V_{INPEAK(MAX)}=373.352[V]
\end{eqnarray}
ここでディレーティングを80%とすると、入力コンデンサの必要定格電圧V_CIN(RATED)は以下の値となります。
\begin{eqnarray}
V_{CIN(RATED)}=\frac{V_{CIN(MAX)}}{0.8}=466.690[V]
\end{eqnarray}

入力コンデンサの容量の導出

入力コンデンサの容量の導出方法には2つの設計方法があります。

設計方法１

設計方法1では、最大入力電流(実効値)I_INRMS(MAX)と最小入力電圧(実効値)V_INRMS(MIN)を用いた設計です。まず、最小入力電圧(実効値)V_INRMS(MIN)のリプル率rを決めます。リプル率rは一般的には1%～10%の間に設定します。ここではrを10%(0.1)として設計をします。この場合、入力コンデンサの容量は以下の値となります。
\begin{eqnarray}
C_{IN}={\%}RIPPLE×\frac{I_{INRMS(MAX)}}{2{\pi}f_{SW}rV_{INRMS(MIN)}}=0.734[uF]
\end{eqnarray}

設計方法２

設計方法2では、まずインダクタリプル電流I_LRIPPLEと入力コンデンサ電圧のリプル電圧V_CINRIPPLEを用いた設計です。
インダクタリプル電流I_LRIPPLEは以下の式で求めることができます。
\begin{eqnarray}
I_{LRIPPLE}={\%}RIPPLE×I_{INPEAK(MAX)}
\end{eqnarray}
また、入力コンデンサ電圧のリプル電圧V_CINRIPPLEは以下の式で求めることができます(ブリッジダイオードの順方向電圧は入力コンデンサ電圧に比べて十分小さいため省略しています)。リプル率rは一般的には1%～10%の間に設定します。ここではrを10%(0.1)として設計をします。
\begin{eqnarray}
V_{CINRIPPLE}=r×V_{INPEAK(MIN)}
\end{eqnarray}
上式のインダクタリプル電流I_LRIPPLEと入力コンデンサ電圧のリプル電圧V_CINRIPPLEを用いると、入力コンデンサの容量は以下の値となります。
\begin{eqnarray}
C_{IN}=\frac{I_{LRIPPLE}}{8f_{SW}V_{CINRIPPLE}}=0.577 [uF]
\end{eqnarray}

上記の設計で求めた入力コンデンサC_INの容量に近い値を選定します。この時、入力コンデンサC_INの容量が大きいほど、EMIフィルタを小さくすることができますが、電流歪みが発生するため、力率が低下します(特に高入力電圧＆高負荷時に力率が低下します)。

補足：インダクタンスLの設計式の導出方法

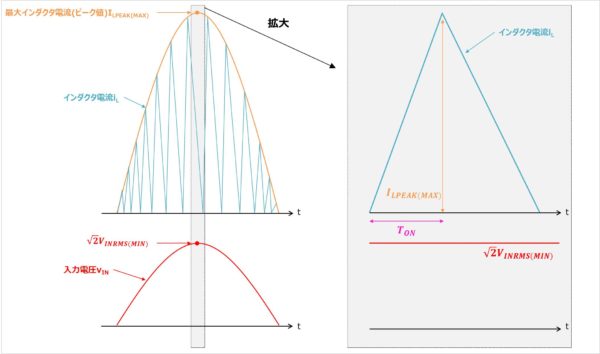
BCMモードにおいて、入力電圧v_INのピーク時にPFC回路の最小オンデューティ比D_MINとなります。そのため、最小オンデューティ比D_MINは以下の式で求めることができます。下式ではブリッジダイオードの順方向電圧V_Fは無視しています。
\begin{eqnarray}
D_{MIN}=\frac{V_{OUT}-\sqrt{2}V_{INRMS(MIN)}}{V_{OUT}}
\end{eqnarray}
また、オン時間T_ONは以下の式で求めることができます。
\begin{eqnarray}
T_{ON}=\frac{D_{MIN}}{f_{SW(MIN)}}
\end{eqnarray}
このオン時間T_ONにおいて、インダクタに流れる電流が0AからI_LPEAK(MAX)まで増加する必要があります。したがって、インダクタの有名な式\(v=L\displaystyle\frac{di}{dt}\)を用いると、インダクタンスLは以下の式となり、インダクタンスLの設計式を導出することができます。
\begin{eqnarray}
L=\frac{\sqrt{2}V_{INRMS(MIN)}}{I_{LPEAK(MAX)}}T_{ON}=\frac{{\eta}×{\cos}{\varphi}×{V_{INRMS(MIN)}}^2×(V_{OUT}-\sqrt{2} V_{INRMS(MIN)})}{2×P_{OUT}×V_{OUT}×f_{SW(MIN)}}
\end{eqnarray}

補足：出力コンデンサC_OUTの設計式の導出方法

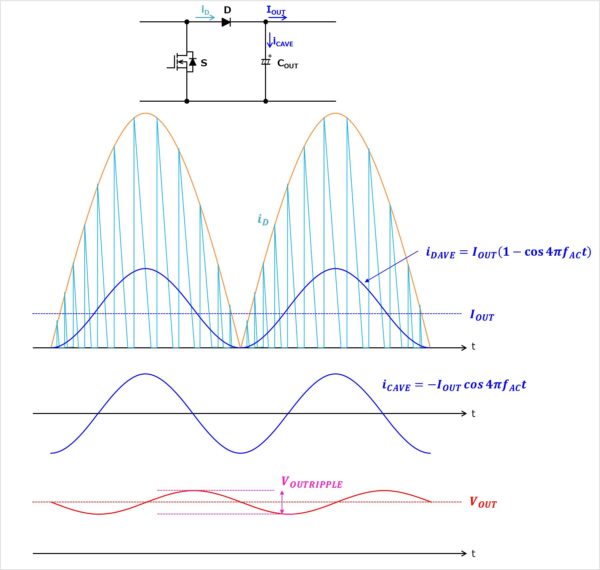
ダイオードに流れる電流の平均電流i_DAVEは以下の式で表すことができます。
\begin{eqnarray}
i_{DAVE}= I_{OUT}(1-{\cos}4{\pi}f_{AC}t)
\end{eqnarray}
出力コンデンサには上式から出力電流I_OUTを引いた値が流れるため、出力コンデンサに流れる電流の平均電流i_CAVE以下の式となります。
\begin{eqnarray}
i_{CAVE}=-I_{OUT}{\cos}4{\pi}f_{AC}t
\end{eqnarray}
この電流によって出力電圧にはリプルが生じます。上図より、\(t=\displaystyle\frac{1}{8 f_{AC}}\)から\(t=\displaystyle\frac{3}{8 f_{AC}}\)の期間で出力電圧V_OUTRIPPLEが増加するため、以下の式となり、出力コンデンサC_OUTの設計式の導出することができます。
\begin{eqnarray}
V_{OUTRIPPLE}&=&\frac{1}{C_{OUT}}\displaystyle\int_{\frac{1}{8 f_{AC}}}^{\frac{3}{8 f_{AC}}}-I_{OUT}{\cos}4{\pi}f_{AC}t dt\\
&=&\frac{I_{OUT}}{4{\pi}f_{AC}}\left[-{\sin}4{\pi}f_{AC}t \right]_ {\frac{1}{8 f_{AC}}}^{\frac{3}{8 f_{AC}}}\\
&=&\frac{I_{OUT}}{ C_{OUT}4{\pi}f_{AC}}\left(-{\sin}\frac{3}{2}{\pi}+{\sin}\frac{1}{2}{\pi} \right)\\
&=&\frac{I_{OUT}}{ C_{OUT}2{\pi}f_{AC}}
\end{eqnarray}
上式を変形すると、
\begin{eqnarray}
C_{OUT}＝\frac{I_{OUT}}{2{\pi}f_{AC} V_{OUTRIPPLE}}
\end{eqnarray}
となります。