この記事では『誘電率』について図を用いて詳しく説明してます。
誘電率とは

面積\(S{\mathrm{[m^2]}}\)の2つの電極板を距離\(d{\mathrm{[m]}}\)離して平行においたコンデンサの静電容量\(C{\mathrm{[F]}}\)は面積\(S\)に比例し、距離\(d\)に反比例します。ここで比例定数を\({\varepsilon}\)とすると、コンデンサの静電容量\(C\)は次式で表されます。
\begin{eqnarray}
C={\varepsilon}\frac{S}{d}{\mathrm{[F]}}\tag{1}
\end{eqnarray}
この比例定数\({\varepsilon}\)を誘電率といいます。\({\varepsilon}\)はギリシャ文字であり「イプシロン」と読みます。(1)式より、誘電率\({\varepsilon}\)が大きいほど、静電容量\(C\)が大きくなることが分かります。
また「\(Q=CV\)」の式より、静電容量\(C\)が大きいということは、電荷\(Q\)をたくさん蓄えられるということになります。つまり、誘電率\({\varepsilon}\)が大きいほど、電荷\(Q\)を蓄えやすいということになります。
ポイント
- 誘電率\({\varepsilon}\)はギリシャ文字であり「イプシロン」と読む。
- 誘電率\({\varepsilon}\)が大きいほど、静電容量\(C\)が大きくなる(電荷\(Q\)を蓄えやすくなる)。
補足
誘電率は英語では『Permittivity』と書きます。
誘電率の単位
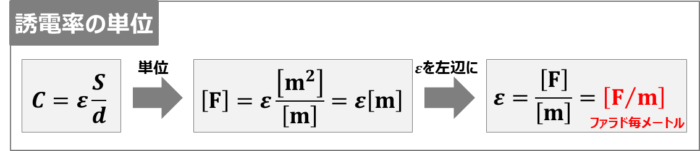
(1)式より誘電率の単位は以下のように変形できるため、誘電率の単位には\({\mathrm{[F/m]}}\)(←ファラド毎メートル)を用います。
\begin{eqnarray}
{\mathrm{[F]}}&=&{\varepsilon}\frac{{\mathrm{[m^2]}}}{{\mathrm{[m]}}}\\
&=&{\varepsilon}{\mathrm{[m]}}\\
{\Leftrightarrow}{\varepsilon}&=&\frac{{\mathrm{[F]}}}{{\mathrm{[m]}}}\tag{2}
\end{eqnarray}
\({\mathrm{[F/m]}}\)の\({\mathrm{[F]}}\)は静電容量\(C\)の単位から決めれられているのです。
ポイント
- 誘電率の単位には\({\mathrm{[F/m]}}\)(←ファラド毎メートル)を用いる。
真空の誘電率
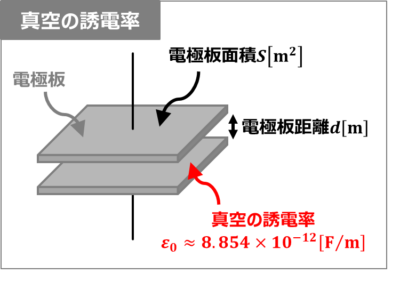
真空の誘電率の記号は誘電率\({\varepsilon}\)に「\(0\)」を付けて「\({\varepsilon}_0\)」と書きます。
真空の誘電率\({\varepsilon}_0\)の大きさは、以下の値となります。
\begin{eqnarray}
{\varepsilon}_0{\;}{\approx}{\;}8.854×10^{-12}{\mathrm{[F/m]}}\tag{3}
\end{eqnarray}
クーロンの法則
少し話がずれますが、クーロンの法則に真空の誘電率\({\varepsilon}_0\)が出てくるので説明します。
クーロンの法則の公式は次式で表されます。
\begin{eqnarray}
F=k\frac{Q_{A}Q_{B}}{r^2}\tag{4}
\end{eqnarray}
(4)式に出てくる比例定数\(k\)は以下の式で表されます。
\begin{eqnarray}
k=\frac{1}{4{\pi}{\varepsilon}_{0}}\tag{5}
\end{eqnarray}
ここで、比例定数\(k\)の式中にある\({\pi}\)は円周率の\({\pi}\)であり「\({\pi}=3.14{\cdots}\)」、\({\varepsilon}_0\)は真空の誘電率であり「\({\varepsilon}_0{\;}{\approx}{\;}8.854×10^{-12}\)」となるため、比例定数\(k\)の値は真空中では以下の値となります。
\begin{eqnarray}
k=\frac{1}{4{\pi}{\varepsilon}_{0}}{\;}{\approx}{\;}9×10^{9}{\mathrm{[N{\cdot}m^2/C^2]}}\tag{6}
\end{eqnarray}
誘電率が大きい場合には、比例定数\(k\)が小さくなるため、クーロン力\(F\)が小さくなるということも分かりますね。
なお、『クーロンの法則』については下記の記事で詳しく説明していますのでご参考にしてください。
-

【クーロンの法則】『公式』や『比例定数』や『歴史』などを解説!
続きを見る
ポイント
- 真空の誘電率\({\varepsilon}_0\)の大きさは「\({\varepsilon}_0{\;}{\approx}{\;}8.854×10^{-12}{\mathrm{[F/m]}}\)」である。
比誘電率とは


比誘電率の記号は誘電率\({\varepsilon}\)に「\(r\)」を付けて「\({\varepsilon}_r\)」と書きます。
比誘電率\({\varepsilon}_r\)は真空の誘電率\({\varepsilon}_0\)を1とした時のある誘電体の誘電率\({\varepsilon}\)を表したものであり、次式で表されます。
\begin{eqnarray}
{\varepsilon}_r=\frac{{\varepsilon}}{{\varepsilon}_0}\tag{7}
\end{eqnarray}
比誘電率\({\varepsilon}_r\)は物質により異なります。例えば、紙の比誘電率\({\varepsilon}_r\)はほぼ2となっています。そのため、紙の誘電率\({\varepsilon}\)は(7)式に代入すると以下のように求めることができます。
\begin{eqnarray}
{\varepsilon}&=&{\varepsilon}_r{\varepsilon}_0\\
&=&2×8.854×10^{-12}\\
&=&17.71×10^{-12}{\mathrm{[F/m]}}\tag{8}
\end{eqnarray}
なお、空気の比誘電率\({\varepsilon}_r\)はほぼ1なので、空気の誘電率\({\varepsilon}\)は真空の誘電率\({\varepsilon}_0\)とほぼ同じになります。
その他の物質としては、ゴムの比誘電率\({\varepsilon}_r\)は約2、陶器の比誘電率\({\varepsilon}_r\)は約6、水の比誘電率\({\varepsilon}_r\)は約60となっています。コンデンサによく用いられるチタン酸バリウムの比誘電率\({\varepsilon}_r\)は約5000となります。
比誘電率\({\varepsilon}_r\)は「比」なので単位はありません。
補足
- 比誘電率は英語では『Relative Permittivity』と書きます。
- 誘電率は誘電体の誘電分極のしやすさを表します。誘電分極しやすい物質ほど比誘電率\({\varepsilon}_r\)が大きくなります。誘電分極については下記の記事で詳しく説明していますのでご参考にしてください。
-


【静電誘導と誘電分極】違いと仕組みをわかりやすく解説!
続きを見る
-
ポイント
- 比誘電率\({\varepsilon}_r\)は真空の誘電率\({\varepsilon}_0\)を1とした時のある誘電体の誘電率\({\varepsilon}\)を表したものである。
- 誘電率は誘電体の誘電分極のしやすさを表す。
誘電体とコンデンサ
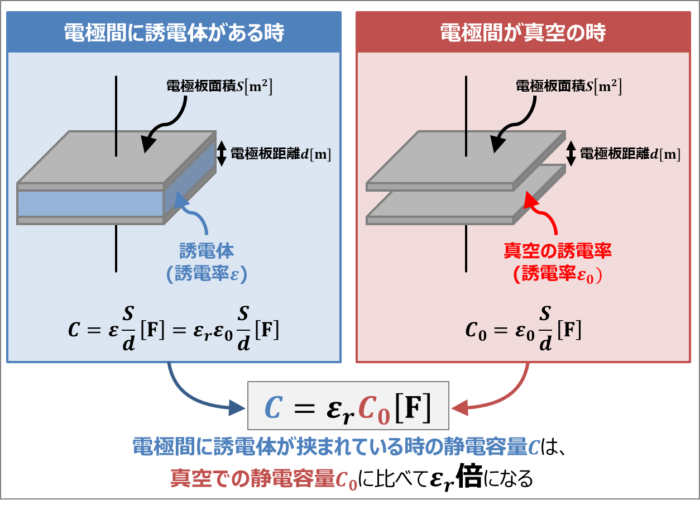

(7)式を変形した「\({\varepsilon}={\varepsilon}_r{\varepsilon}_0\)」を(1)式に代入すると、次式となります。
\begin{eqnarray}
C={\varepsilon}_r{\varepsilon}_0\frac{S}{d}{\mathrm{[F]}}\tag{9}
\end{eqnarray}
真空での静電容量を「\(C_0={\varepsilon}_0\displaystyle\frac{S}{d}\)」とすると、(9)式は次式となります。
\begin{eqnarray}
C={\varepsilon}_rC_0{\mathrm{[F]}}\tag{10}
\end{eqnarray}
つまり、2つの電極板の面積\(S{\mathrm{[m^2]}}\)と距離\(d{\mathrm{[m]}}\)が変わらない時(つまり、コンデンサの形が変わらない時)、電極間に誘電体が挟まれている時の静電容量\(C\)は、真空での静電容量\(C_0\)に比べて\({\varepsilon}_r\)倍になるということが分かります。電極間に挟まれている誘電体の比誘電率\({\varepsilon}_r\)が2の場合、静電容量\(C\)は真空での静電容量\(C_0\)と比べると2倍になるということです。
また、(10)式を「\(Q=CV\)」に代入すると、次式となります。
\begin{eqnarray}
Q={\varepsilon}_rC_0V\tag{11}
\end{eqnarray}
真空の時の式「\(Q_0=C_0V_0\)」と比較すると、電極間に誘電体を挿入することにより、以下の特徴となることが分かります。
- 電荷\(Q\)が一定の場合、コンデンサにかかる電圧\(V\)が「\(\displaystyle\frac{1}{{\varepsilon}_r}\)倍」になる。
- 電圧\(V\)が一定の場合、コンデンサに蓄えられる電荷\(Q\)が「\({\varepsilon}_r\)倍」になる。
電極間に誘電体が挟まれている時の式「\(Q={\varepsilon}_rC_0V\)」と真空の時の式「\(Q_0=C_0V_0\)」において、電荷\(Q\)を一定にすると(\(Q=Q_0\)にすると)、
\begin{eqnarray}
{\varepsilon}_rC_0V&=&C_0V_0\\
{\Leftrightarrow}V&=&\frac{1}{{\varepsilon}_r}V_0\tag{12}
\end{eqnarray}
となり、電極間に誘電体を挟むとコンデンサにかかる電圧\(V\)が真空の時の電圧\(V_0\)の「\(\displaystyle\frac{1}{{\varepsilon}_r}\)倍」になることが分かります。
電極間に誘電体が挟まれている時の式「\(Q={\varepsilon}_rC_0V\)」と真空の時の式「\(Q_0=C_0V_0\)」において、電圧\(V\)を一定にすると(\(V=V_0\)にすると)、
\begin{eqnarray}
\frac{Q}{{\varepsilon}_rC_0}&=&\frac{Q_0}{C_0}\\
{\Leftrightarrow}Q&=&{\varepsilon}_rQ_0\tag{13}
\end{eqnarray}
となり、電極間に誘電体を挟むとコンデンサに蓄えられる電荷\(Q\)が真空の時の電荷\(Q_0\)の「\({\varepsilon}_r\)倍」になることが分かります。
ではこの特徴を実際に確認してみましょう。
コンデンサを充電後、電池をつなげずに誘電体を挿入する
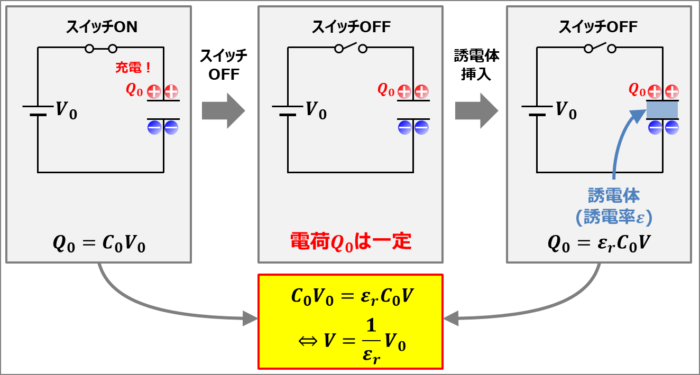

真空中において上図に示すように電圧\(V_0\)の電池、スイッチ、コンデンサ(真空での静電容量\(C_0\))を直列接続します。この状態において、スイッチをONすると、コンデンサが充電され電荷\(Q_0\)が蓄えられます。コンデンサに蓄えられている電荷\(Q_0\)は次式で表されます。
\begin{eqnarray}
Q_0=C_0V_0\tag{14}
\end{eqnarray}
ここで、コンデンサを充電してある状態からスイッチをOFFさせます。スイッチをOFFすることにより、電池から電荷の供給を受けることができなくなり、コンデンサに蓄えられている電荷\(Q_0\)は一定となります。
この状態で比誘電率が\({\varepsilon}_r\)の誘電体をコンデンサに挿入すると、静電容量が\(C_0\)から\({\varepsilon}_rC_0\)に変化します。
そのため、コンデンサに蓄えられている電荷\(Q_0\)は次式で表されます。
\begin{eqnarray}
Q_0={\varepsilon}_rC_0V\tag{15}
\end{eqnarray}
(14)式と(15)式を比較すると、以下の式が成り立ちます。
\begin{eqnarray}
{\varepsilon}_rC_0V&=&C_0V_0\\
{\Leftrightarrow}V&=&\frac{1}{{\varepsilon}_r}V_0\tag{16}
\end{eqnarray}
以上より、コンデンサに電池が接続されていない状態で、電極間に誘電体を挟むと、コンデンサにかかる電圧\(V\)が真空の時の電圧\(V_0\)の「\(\displaystyle\frac{1}{{\varepsilon}_r}\)倍」になることが分かります。
ポイント
コンデンサを充電後、電池をつなげずに誘電体を挿入すると、コンデンサに蓄えられている電荷\(Q_0\)は一定で、静電容量は「\({\varepsilon}_r\)倍」、コンデンサにかかる電圧は「\(\displaystyle\frac{1}{{\varepsilon}_r}\)倍」となる。
コンデンサを充電後、電池をつなげたまま誘電体を挿入する
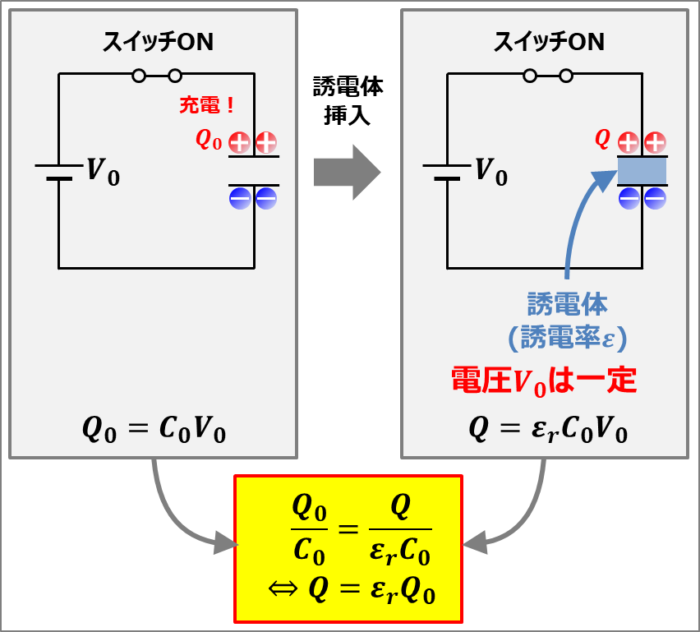

真空中において上図に示すように電圧\(V_0\)の電池、スイッチ、コンデンサ(真空での静電容量\(C_0\))を直列接続します。この状態において、スイッチをONすると、コンデンサが充電され電荷\(Q_0\)が蓄えられます。コンデンサに蓄えられている電荷\(Q_0\)は次式で表されます。
\begin{eqnarray}
Q_0=C_0V_0\tag{17}
\end{eqnarray}
ここで、コンデンサを充電してある状態のまま比誘電率が\({\varepsilon}_r\)の誘電体をコンデンサに挿入すると、静電容量が\(C_0\)から\({\varepsilon}_rC_0\)に変化します。また、スイッチがONのため、コンデンサに印加されている電圧\(V_0\)は一定となります。
そのため、コンデンサに蓄えられている電荷\(Q_0\)は次式で表されます。
\begin{eqnarray}
Q={\varepsilon}_rC_0V_0\tag{18}
\end{eqnarray}
(17)式と(18)式を比較すると、以下の式が成り立ちます。
\begin{eqnarray}
\frac{Q}{{\varepsilon}_rC_0}&=&\frac{Q_0}{C_0}\\
{\Leftrightarrow}Q&=&{\varepsilon}_rQ_0\tag{19}
\end{eqnarray}
以上より、コンデンサに電池が接続されている状態で、電極間に誘電体を挟むと、コンデンサに蓄えられる電荷\(Q\)が真空の時の電荷\(Q_0\)の「\({\varepsilon}_r\)倍」になることが分かります。
ポイント
コンデンサを充電後、電池をつなげたまま誘電体を挿入すると、コンデンサに印加されている電圧\(V_0\)は一定で、静電容量は「\({\varepsilon}_r\)倍」、コンデンサに蓄えられる電荷は「\({\varepsilon}_r\)倍」となる。
誘電体を挿入することによる静電容量の変化
面積\(S{\mathrm{[m^2]}}\)の2つの電極板を距離\(d{\mathrm{[m]}}\)離して平行においたコンデンサにおいて、2つの電極板との間に誘電率\({\varepsilon}\)の誘電体を挟む時、コンデンサの静電容量\(C\)は次式で表されます。
\begin{eqnarray}
C={\varepsilon}\frac{S}{d}={\varepsilon}_r{\varepsilon}_0\frac{S}{d}{\mathrm{[F]}}\tag{20}
\end{eqnarray}
ではここで、誘電体をコンデンサの一部(直列or並列)に挿入することにより、静電容量\(C\)がどのように変化するかを説明します。
コンデンサに誘電体を直列に挿入することによる静電容量の変化
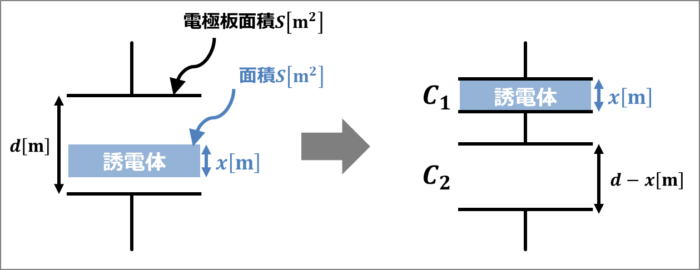

面積\(S{\mathrm{[m^2]}}\)の2つの電極板を距離\(d{\mathrm{[m]}}\)離して平行においたコンデンサにおいて、2つの電極板との間に面積が\(S{\mathrm{[m^2]}}\)、厚さが\(x{\mathrm{[m]}}\)、誘電率\({\varepsilon}\)の誘電体を挟んでいるとします。
この時、静電容量\(C\)はコンデンサを直列接続した場合の合成容量になります。
誘電体が挟まれている方の静電容量\(C_1\)は次式となります。
\begin{eqnarray}
C_1={\varepsilon}_r{\varepsilon}_0\frac{S}{x}{\mathrm{[F]}}\tag{21}
\end{eqnarray}
誘電体が挟まれてない方の静電容量\(C_2\)は次式となります。
\begin{eqnarray}
C_2={\varepsilon}_0\frac{S}{d-x}{\mathrm{[F]}}\tag{22}
\end{eqnarray}
コンデンサを直列接続している場合、合成容量\(C\)の逆数は各々の静電容量の逆数の和となります。そのため、合成容量\(C\)は次式となります。
\begin{eqnarray}
\frac{1}{C}&=&\frac{1}{C_1}+\frac{1}{C_2}\\
&=&\frac{1}{{\varepsilon}_r{\varepsilon}_0\displaystyle\frac{S}{x}}+\frac{1}{{\varepsilon}_0\displaystyle\frac{S}{d-x}}\\
&=&\frac{x}{{\varepsilon}_r{\varepsilon}_0S}+\frac{d-x}{{\varepsilon}_0S}\\
&=&\frac{x}{{\varepsilon}_r{\varepsilon}_0S}+\frac{{\varepsilon}_r(d-x)}{{\varepsilon}_r{\varepsilon}_0S}\\
&=&\frac{x+{\varepsilon}_r(d-x)}{{\varepsilon}_r{\varepsilon}_0S}\\
{\Leftrightarrow}C&=&\frac{{\varepsilon}_r{\varepsilon}_0S}{x+{\varepsilon}_r(d-x)}\tag{23}
\end{eqnarray}
コンデンサに誘電体を並列に挿入することによる静電容量の変化
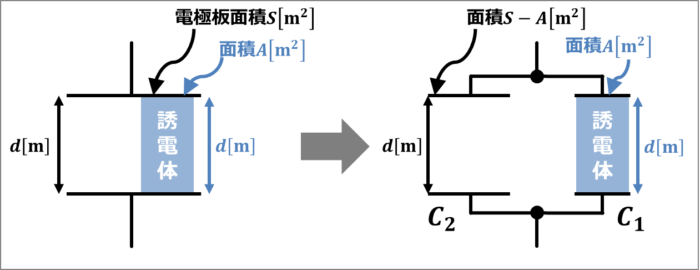

面積\(S{\mathrm{[m^2]}}\)の2つの電極板を距離\(d{\mathrm{[m]}}\)離して平行においたコンデンサにおいて、2つの電極板との間に面積が\(A{\mathrm{[m^2]}}\)、厚さが\(d{\mathrm{[m]}}\)、誘電率\({\varepsilon}\)の誘電体を挟んでいるとします。
この時、静電容量\(C\)はコンデンサを並列接続した場合の合成容量になります。
誘電体が挟まれている方の静電容量\(C_1\)は次式となります。
\begin{eqnarray}
C_1={\varepsilon}_r{\varepsilon}_0\frac{A}{d}{\mathrm{[F]}}\tag{24}
\end{eqnarray}
誘電体が挟まれてない方の静電容量\(C_2\)は次式となります。
\begin{eqnarray}
C_2={\varepsilon}_0\frac{S-A}{d}{\mathrm{[F]}}\tag{25}
\end{eqnarray}
コンデンサを並列接続している場合、合成容量\(C\)は各々の静電容量の和となります。そのため、合成容量\(C\)は次式となります。
\begin{eqnarray}
C&=&C_1+C_2\\
&=&{\varepsilon}_r{\varepsilon}_0\frac{A}{d}+{\varepsilon}_0\frac{S-A}{d}\\
&=&\frac{{\varepsilon}_r{\varepsilon}_0A+{\varepsilon}_0(S-A)}{d}\tag{26}
\end{eqnarray}
誘電率εと透磁率μ
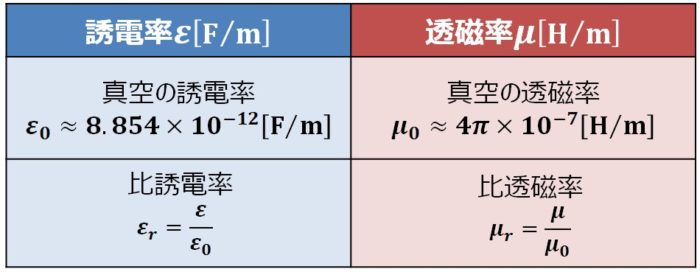

誘電率\({\varepsilon}\)は誘電体の誘電分極のしやすさを表しています。一方、透磁率\({\mu}\)は物質の磁束の通りやすさ(磁化のしやすさ)を表しています。
この誘電率\({\varepsilon}\)と透磁率\({\mu}\)はとても似ている関係なのです。
誘電率\({\varepsilon}\)には『真空の誘電率\({\varepsilon}_0{\;}{\approx}{\;}8.854×10^{-12}{\mathrm{[F/m]}}\)』を1とした時のある誘電体の誘電率\({\varepsilon}\)を表した比誘電率\({\varepsilon}_r\)があることを説明しました。
一方、透磁率\({\mu}\)にも『真空の透磁率\({\mu}_0{\;}{\approx}{\;}4π×10^{-7}{\mathrm{[F/m]}}\)』を1とした時のある物質の透磁率\({\mu}\)を表した比透磁率\({\mu}_r\)があります。
誘電率\({\varepsilon}\)と透磁率\({\mu}\)を整理すると上図のようになります。
透磁率\({\mu}\)については別途下記の記事で詳しく説明していますのでご参考にしてください。
-



【透磁率のまとめ】比透磁率や単位などを詳しく説明します!
続きを見る
まとめ
この記事では『誘電率』について、以下の内容を説明しました。
当記事のまとめ
- 誘電率とは
- 誘電率の単位
- 真空の誘電率
- 比誘電率
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。







