ICのスパイスモデルやSPICEの参考書等を見ると、サブサーキット名がXFMRとなっているトランスのネットリストがあります。
このXFMRはトランスをビヘイビア電源(bi,bv)を用いて再現したものであり、理想トランスとなっています。
この記事では、ビヘイビア電源(bi,bv)を用いたトランスの『等価回路』と『ネットリスト(XFMR)』について説明します。
理想トランス
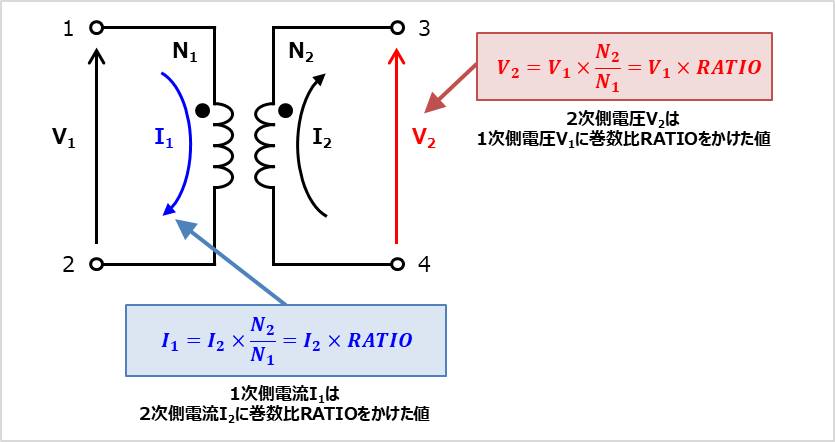
ICのデータシートや参考書に記載されているトランスのネットリスト(XFMRと書いてある場合が多い)は理想トランスとなっているので、まず、理想トランスについて説明します。
理想トランスは結合係数が1(完全に結合)、漏れインダクタンスなし、励磁インダクタンスが無限大で一次二次が絶縁されているトランスです。また、実際のトランスと異なり、直流も通すことができる仮想のトランスとなります。この理想トランスはSPICEにおいてAC-DCコンバータの動作をモデル化するのに役立ちます。
上図の回路の場合、2次側電圧V2は1次側電圧V1に巻数比RATIOをかけた値となり、
\begin{eqnarray}
V_2= V_1×\frac{N_2}{N_1}=V_1×RATIO
\end{eqnarray}
となります。
また、1次側電流I1は2次側電流I2に巻数比RATIOをかけた値となり、
\begin{eqnarray}
I_1= I_2×\frac{N_2}{N_1}=I_2×RATIO
\end{eqnarray}
となります。この関係をビヘイビア電源(bi,bv)を用いて等価回路とネットリストで再現します。
『等価回路』と『ネットリスト(XFMR)』
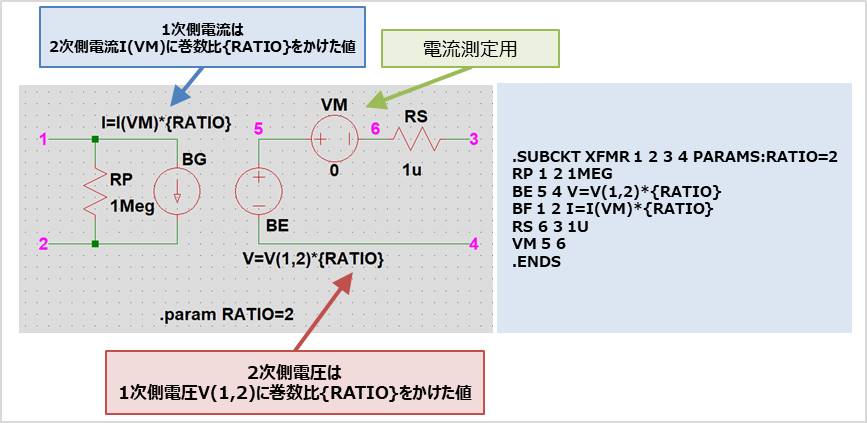
理想トランスのLTspiceにおける等価回路は上図のようになります。
電圧源VMは2次側電流測定用なので電圧値は「0」となっています。また、抵抗RPとRSはシミュレーション実行時にエラーなるのを防ぐために接続されます。RATIOは巻数比となっています。
ビヘイビア電源BEは二次側電圧を作成する電源です。2次側電圧は1次側電圧V(1,2)に巻数比{RATIO}をかけた値となるため、
\begin{eqnarray}
V= V(1,2)×\{RATIO\}
\end{eqnarray}
となります。
ビヘイビア電源BGは1次側電流を作成する電源です。1次側電流は2次側電流I(VM)に巻数比{RATIO}をかけた値となるため、
\begin{eqnarray}
I= I(VM)×\{RATIO\}
\end{eqnarray}
となります。
この回路図をネットリストで表すと、以下のようになります。
.SUBCKT XFMR 1 2 3 4 PARAMS:RATIO=2
RP 1 2 1MEG
BE 5 4 V=V(1,2)*{RATIO}
BG 1 2 I=I(VM)*{RATIO}
RS 6 3 1U
VM 5 6
.ENDS
シミュレーション
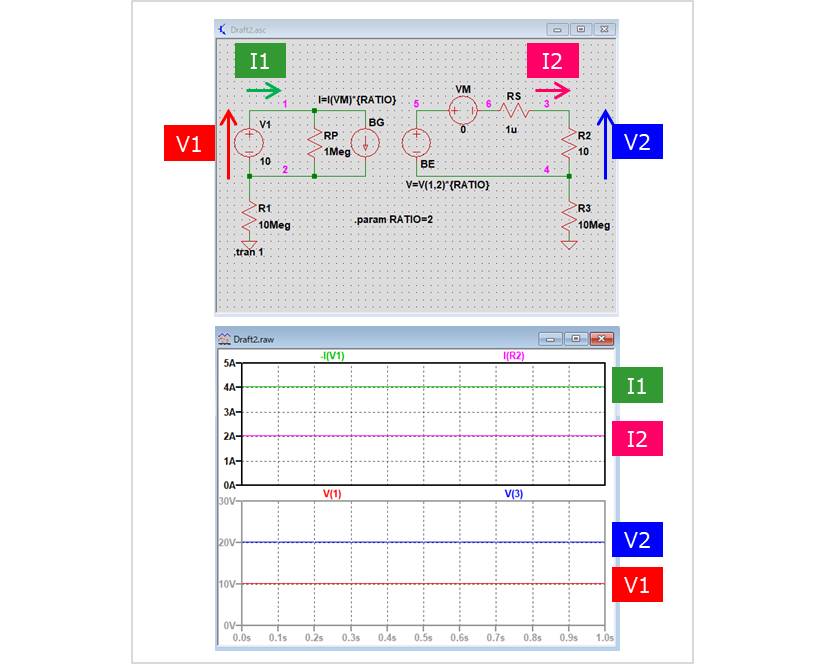
巻数比RATIOを2、一次側電圧V1を10V、二次側に抵抗R2(10Ω)を接続した時のシミュレーションしてみます。抵抗R2とR3はシミュレーションにおけるエラーを防止するための抵抗です。シミュレーションにおいてGNDを接続しないと、エラーとなります。10Megという大きな抵抗値の抵抗を接続することで、疑似的にGNDから浮かせています。
ビヘイビア電源BEは、
\begin{eqnarray}
V= V(1,2)×\{RATIO\}=10×2=20
\end{eqnarray}
となるため、二次側電圧V2は20Vとなります。また、2次側電流I2は、二次側電圧V2が20Vで、抵抗R2が10Ωなので、2Aとなります。
また、ビヘイビア電源BIは、
\begin{eqnarray}
I= I(VM)×\{RATIO\}=2×2=4
\end{eqnarray}
となるため、一次側電流I1は4Aとなります。
【補足】補助巻線を再現する場合
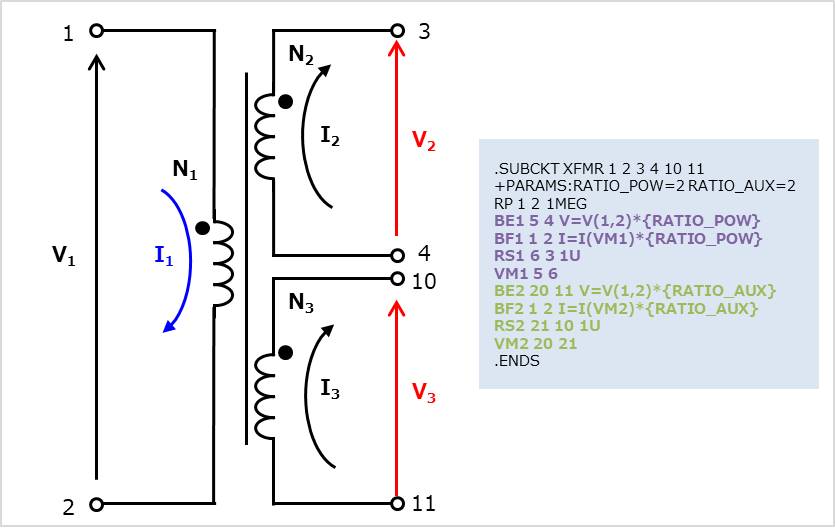
上図のように記載することで補助巻線も再現することができます。
ネットリストで表すと以下のようになります。
.SUBCKT XFMR 1 2 3 4 10 11 PARAMS:RATIO_POW=2 RATIO_AUX=2
RP 1 2 1MEG
BE1 5 4 V=V(1,2)*{RATIO_POW}
BG1 1 2 I=I(VM1)*{RATIO_POW}
RS1 6 3 1U
VM1 5 6
BE2 20 11 V=V(1,2)*{RATIO_AUX}
BG2 1 2 I=I(VM2)*{RATIO_AUX}
RS2 21 10 1U
VM2 20 21
.ENDS






