昇降圧コンバータ(昇降圧チョッパ)とは？原理などを解説！

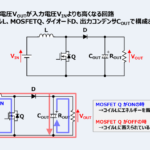
この記事では『昇降圧コンバータ』について

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

昇降圧コンバータ(昇降圧チョッパ)とは

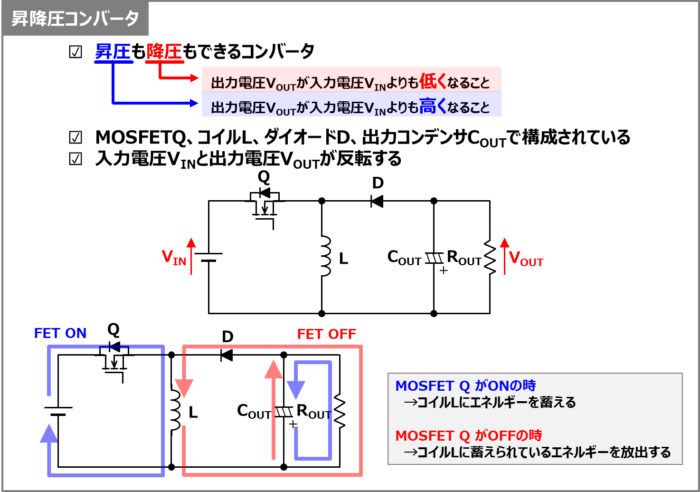
昇降圧コンバータはその名の通り、昇圧も降圧もできるコンバータです。MOSFET\(Q\)、コイル(インダクタ)\(L\)、ダイオード\(D\)、出力コンデンサ\(C_{OUT}\)で構成されています。

昇圧するか降圧するかは、MOSFET\(Q\)のオンデューティ比\(D\)(1周期\(T\)におけるオン期間\(T_{ON}\)の割合)によって決まります。

昇降圧コンバータは、MOSFET\(Q\)がONの時にコイル\(L\)にエネルギーを蓄えます。コイル\(L\)にエネルギーを蓄える期間が長いほど、出力電圧\(V_{OUT}\)を高くすることができます。

なお、昇降圧コンバータは「入力と出力が反転する」という特徴があるので注意してください。基準電位(GND)に対して、入力電圧\(V_{IN}\)がプラス(正)の時に、出力電圧\(V_{OUT}\)はマイナス(負)になります。

『昇降圧コンバータ』と『昇圧コンバータ』と『降圧コンバータ』の違い

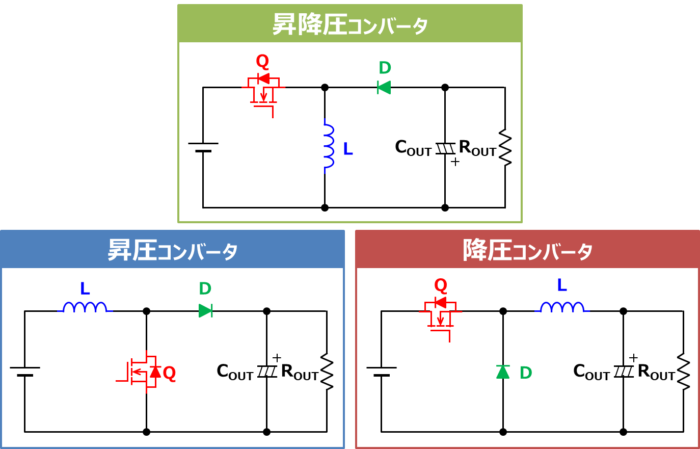
上図に『昇降圧コンバータ』と『昇圧コンバータ』と『降圧コンバータ』の回路図を示しています。

3つのコンバータは全て、MOSFET\(Q\)、コイル\(L\)、ダイオード\(D\)、出力コンデンサ\(C_{OUT}\)で構成されていますが、各部品の接続箇所が異なります。

『昇圧コンバータ』と『昇降圧コンバータ』の回路構成を比較すると、コイル\(L\)とMOSFET\(Q\)の位置が入れ替わり、ダイオード\(D\)の向きが反対になっています。

『降圧コンバータ』と『昇降圧コンバータ』の回路構成を比較すると、コイル\(L\)とダイオード\(D\)の位置が入れ替わっています。

昇降圧コンバータの動作原理

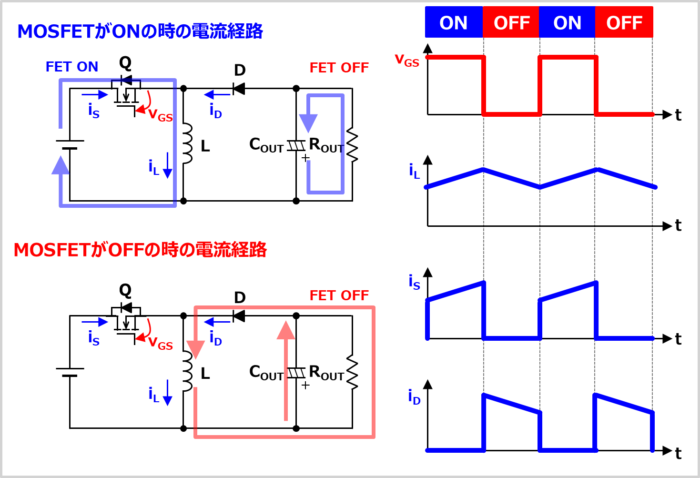
ではこれから、昇降圧コンバータの動作原理について説明します。MOSFET\(Q\)が『ONの時』と『OFFの時』に分けて考えます。

MOSFET\(Q\)がONの時

MOSFET\(Q\)がONの時、電流経路は『入力電圧\(V_{IN}\)→MOSFET\(Q\)→コイル\(L\)』となります。この期間では、出力コンデンサ\(C_{OUT}\)に充電されている電荷が負荷抵抗\(R_{OUT}\)に放電されています。

コイル\(L\)は電流の変化を妨げるように動作するため、MOSFET\(Q\)をONしても、電流は一気には流れず、コイル\(L\)に流れる電流\(i_L\)は徐々に増加します。

コイル\(L\)に電流が流れることで、エネルギーが蓄えられます。

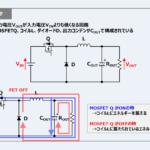
MOSFET\(Q\)がOFFの時

MOSFET\(Q\)がOFFになると、コイル\(L\)に蓄えられているエネルギーを放出して、コイル\(L\)は電流を流し続けようとします。

そのため、この期間の電流経路は『コイル\(L\)→出力部(出力コンデンサ\(C_{OUT}\)＋負荷抵抗\(R_{OUT}\))→ダイオード\(D\)』となります。この期間では、出力コンデンサ\(C_{OUT}\)を充電すると同時に、負荷抵抗\(R_{OUT}\)にも電流が流れています。

コイル\(L\)は電流の変化を妨げるように動作するため、コイル\(L\)に流れる電流\(i_L\)は徐々に減少します。

昇降圧コンバータの出力電圧の式

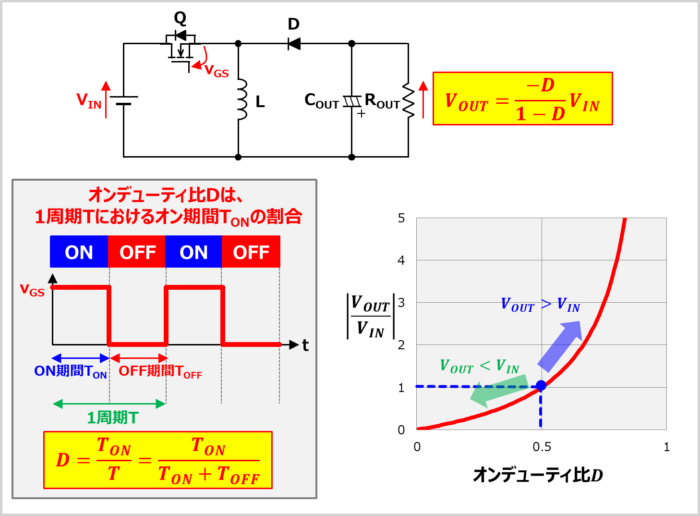
昇降圧コンバータの出力電圧\(V_{OUT}\)は次式となります。

上式において、オンデューティ比\(D\)はMOSFET\(Q\)の1周期\(T\)におけるオン期間\(T_{ON}\)の割合なので、次式で表されます。

\begin{eqnarray}
D=\frac{T_{ON}}{T}=\frac{T_{ON}}{T_{ON}+T_{OFF}}=T_{ON}×f_{SW}\tag{2}
\end{eqnarray}

(2)式において、\(f_{SW}\)はMOSFET\(Q\)のスイッチング周波数です。(2)式から分かるように、オンデューティ比\(D\)は1より小さい値となります。

また、オンデューティ比\(D\)を0～1に変化させた時の\(\left|\displaystyle\frac{V_{OUT}}{V_{IN}}\right|\)のグラフを上図に示しています。

オンデューティ比\(D\)が0.5より大きい時は\(\left|\displaystyle\frac{V_{OUT}}{V_{IN}}\right|\)が1より大きく(\(|V_{OUT}|{>}|V_{IN}|\))、オンデューティ比\(D\)が0.5より小さい時は\(\left|\displaystyle\frac{V_{OUT}}{V_{IN}}\right|\)が1より小さく(\(|V_{OUT}|{<}|V_{IN}|\))なるため、昇降圧できることが式から分かります。

例えば、オンデューティ比\(D\)が0.8の場合と0.2の場合、出力電圧\(V_{OUT}\)は次式で表されます。

\begin{eqnarray}
V_{OUT}&=&\frac{-D}{1-D}V_{IN}=\frac{-0.8}{1-0.8}V_{IN}=-4V_{IN}\tag{3}\\
\\
V_{OUT}&=&\frac{-D}{1-D}V_{IN}=\frac{-0.2}{1-0.2}V_{IN}=-\frac{1}{4}V_{IN}\tag{4}
\end{eqnarray}

上式から分かるように、出力電圧\(V_{OUT}\)の式にマイナスがつきます。すなわち、昇降圧コンバータは昇降圧できますが、「入力と出力が反転する」という特徴があるので注意してください。

昇降圧コンバータのシミュレーション

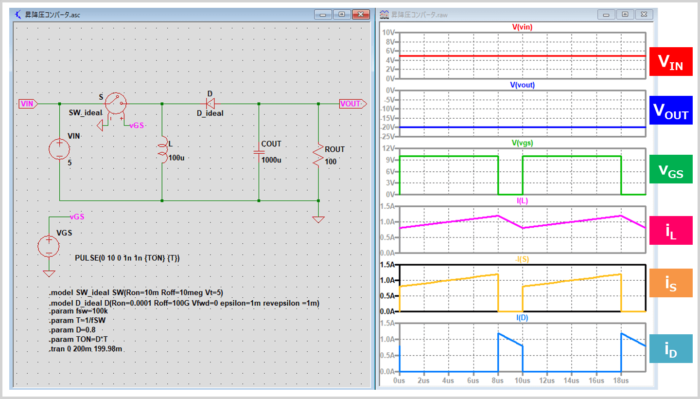
昇降圧コンバータをLTspiceでシミュレーションした時の結果を上図に示しています。

上図の右側に示している波形は上から

となっています。

MOSFET\(Q\)やダイオード\(D\)の損失を無視するために、シミュレーション回路ではMOSFET\(Q\)は理想スイッチ、ダイオード\(D\)は理想ダイオードを用いています。

また、入力電圧\(V_{IN}\)は5V、理想スイッチ\(S\)のオンデューティ比\(D\)は0.8にしています。そのため、出力電圧\(V_{OUT}\)は(1)式より

\begin{eqnarray}
V_{OUT}&=&\frac{-D}{1-D}V_{IN}=\frac{-0.8}{1-0.8}×5=-20{\mathrm{[V]}}
\end{eqnarray}

となります。シミュレーション結果でも、出力電圧\(V_{OUT}\)が-20Vとなり、昇圧動作をしていることが確認できます。

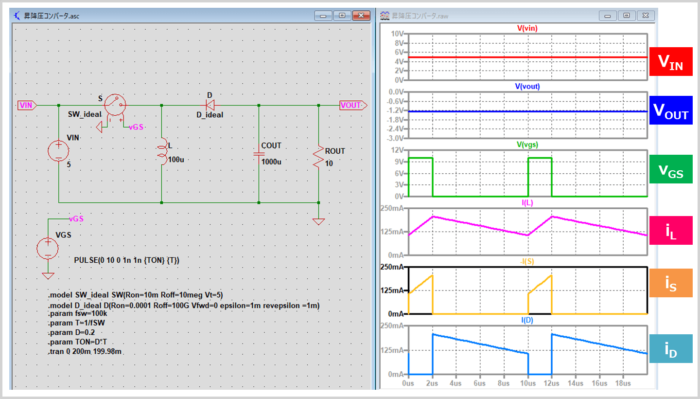
次に、オンデューティ比\(D\)を0.5より小さくした時に、降圧動作をしているかを確認してみましょう。理想スイッチ\(S\)のオンデューティ比\(D\)を0.2にした時のシミュレーション結果を下図に示しています。この場合、出力電圧\(V_{OUT}\)は(1)式より

\begin{eqnarray}
V_{OUT}&=&\frac{-D}{1-D}V_{IN}=\frac{-0.2}{1-0.2}×5=-1.25{\mathrm{[V]}}
\end{eqnarray}

となります。シミュレーション結果でも、出力電圧\(V_{OUT}\)が-1.25Vとなり、降圧動作をしていることが確認できます。

まとめ

この記事では『昇降圧コンバータ』について、以下の内容を説明しました。

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。

全記事一覧

また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。