この記事では『バンドパスフィルタ』について
- バンドパスフィルタとは
- バンドパスフィルタの『中心周波数』と『カットオフ周波数』
- バンドパスフィルタの『周波数特性』
- バンドパスフィルタの『様々な回路』
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
バンドパスフィルタとは
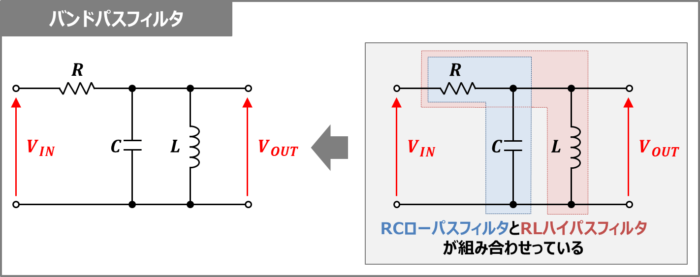
バンドパスフィルタとは、特定の周波数帯域のみを通過させ、それ以外の周波数帯域は減衰させるフィルタのことをいいます。特定の周波数以外の信号をを除去したい時に使用するフィルタです。
バンドパスフィルタは、基本的にはローパスフィルタ(LPF)とハイパスフィルタ(HPF)を組み合わせることで構成することができます。
回路構成には様々な種類がありますが、一例として上図に、抵抗\(R\)、コイル\(L\)、コンデンサ\(C\)で構成されたバンドパスフィルタの回路構成を示しています。コイル\(L\)とコンデンサ\(C\)で並列共振回路を構成しています。上図の回路は『抵抗\(R\)とコンデンサ\(C\)で構成されたRCローパスフィルタ』と『抵抗\(R\)とコイル\(L\)で構成されたRLハイパスフィルタ』を組み合わせることで、バンドパスフィルタを構成しています。
あわせて読みたい
『RCローパスフィルタ』と『RLハイパスフィルタ』については、別途下記の記事で説明していますので、お読みいただければ幸いです。
-

RCローパスフィルタの『伝達関数』や『周波数特性』について
続きを見る
-


RLハイパスフィルタの『伝達関数』や『周波数特性』について
続きを見る
補足
- バンドパスフィルタは英語では『Band-Pass Filter』と書きます。英語の頭文字をとって、『BPF』と表記されることもあります。
- バンドパスフィルタは『帯域通過フィルタ、帯域通過濾波器(ろはき)』とも呼ばれています。
- 特性の周波数帯(バンド)を通過(パス)させるフィルタなので、バンドパスフィルタと呼ばれています。
- バンドパスフィルタとは逆の動作をするフィルタもあります。特定の周波数帯域のみを減衰させ、それ以外の周波数帯域は通過させるフィルタのことを『バンドストップフィルタ(BSF)』といいます。
バンドパスフィルタの『中心周波数』と『カットオフ周波数』
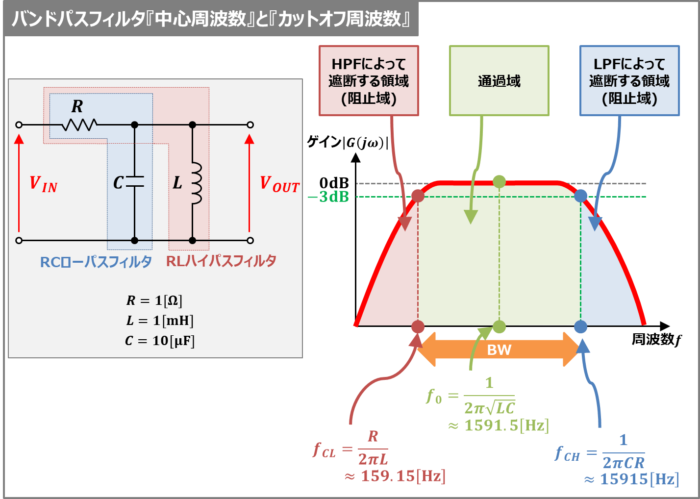

バンドパスフィルタには、下記に示す3つの周波数があります。
- 中心周波数\(f_0\)
- 中心周波数\(f_0\)よりも低いカットオフ周波数\(f_{CL}\)
- 中心周波数\(f_0\)よりも高いカットオフ周波数\(f_{CH}\)
上図に一例として、抵抗\(R=1{\mathrm{[Ω]}}\),コイル\(L=1{\mathrm{[mH]}}\),コンデンサ\(C=10{\mathrm{[μF]}}\)で構成されたバンドパスフィルタを示しています。コイル\(L\)とコンデンサ\(C\)で並列共振回路を構成しています。
上図に示している『LC並列共振回路と抵抗\(R\)で構成されたバンドパスフィルタ』の場合、中心周波数\(f_0\)は『並列共振回路の並列共振周波数(あるいは単に共振周波数)』となり、以下の値となります。
\begin{eqnarray}
f_0=\frac{1}{2{\pi}\sqrt{LC}}=\frac{1}{2{\pi}\sqrt{1×10^{-3}×10×10^{-6}}}{\;}{\approx}{\;}1591.5{\mathrm{[Hz]}}
\end{eqnarray}
中心周波数\(f_0\)よりも低いカットオフ周波数\(f_{CL}\)は『ハイパスフィルタ』のカットオフ周波数となります。上図に示しているバンドパスフィルタでは抵抗\(R\)とコイル\(L\)でハイパスフィルタを構成しており、カットオフ周波数\(f_{CL}\)は以下の値となります。
\begin{eqnarray}
f_{CL}=\frac{R}{2{\pi}L}=\frac{1}{2{\pi}×1×10^{-3}}={\;}{\approx}{\;}159.15{\mathrm{[Hz]}}
\end{eqnarray}
中心周波数\(f_0\)よりも高いカットオフ周波数\(f_{CH}\)は『ローパスフィルタ』のカットオフ周波数となります。上図に示しているバンドパスフィルタでは抵抗\(R\)とコンデンサ\(C\)でローパスフィルタを構成しており、カットオフ周波数\(f_{CH}\)は以下の値となります。
\begin{eqnarray}
f_{CH}=\frac{1}{2{\pi}RC}=\frac{1}{2{\pi}×1×10×10^{-6}}={\;}{\approx}{\;}15915{\mathrm{[Hz]}}
\end{eqnarray}
なお、カットオフ周波数\(f_{CL}\)と\(f_{CH}\)でバンドパスフィルタのバンド幅\(BW\)を求めることができ、以下の値となります。
\begin{eqnarray}
BW=f_{CH}-f_{CL}{\;}{\approx}{\;}15915{\mathrm{[Hz]}}-159.15{\mathrm{[Hz]}}{\;}{\approx}{\;}15756{\mathrm{[Hz]}}
\end{eqnarray}
バンドパスフィルタの中心周波数
バンドパスフィルタの中心周波数\(f_0\)は、次式でも求めることができます。
\begin{eqnarray}
f_0=\sqrt{f_{CL}×f_{CH}}{\;}{\approx}{\;}\sqrt{159.15{\mathrm{[Hz]}}×15915{\mathrm{[Hz]}}}{\;}{\approx}{\;}1591.5{\mathrm{[Hz]}}
\end{eqnarray}
あわせて読みたい
『カットオフ周波数って何?』という方は下記の記事が役に立つと思いますので、ご参考にしてください。
-


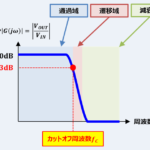
『カットオフ周波数(遮断周波数)』とは?【フィルタ回路】
続きを見る
バンドパスフィルタの『周波数特性』
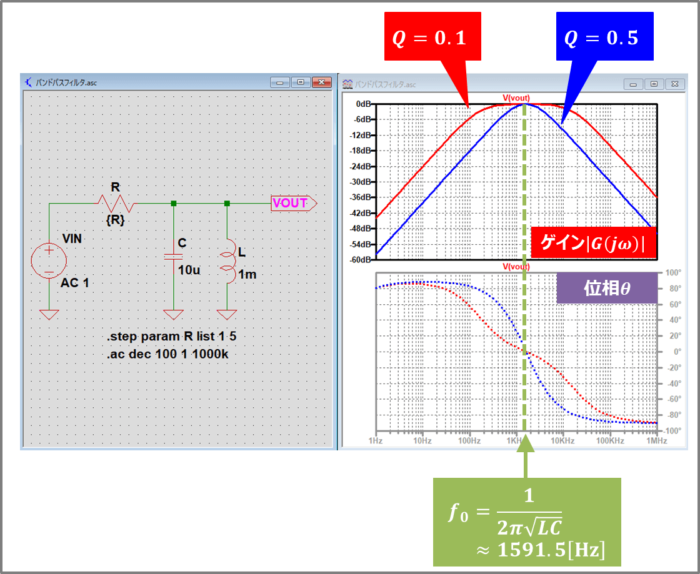

上図に『LC並列共振回路と抵抗\(R\)で構成されたバンドパスフィルタ』の周波数特性を示しています。この周波数特性はLTspiceの『.ac解析』を用いて表示させています。VOUT端子の電圧をプロットすることで、周波数特性を出力することができます。
LTspiceの『.stepコマンド』を用いて抵抗\(R\)の値を\(1{\mathrm{[Ω]}}\)と\(5{\mathrm{[Ω]}}\)で可変させており、赤色の特性と青色の特性は下記のパラメータの時の周波数特性となっています。
- 赤色の特性
- 青色の特性
抵抗\(R=1{\mathrm{[Ω]}}\),コイル\(L=1{\mathrm{[mH]}}\),コンデンサ\(C=10{\mathrm{[μF]}}\)の時の周波数特性
抵抗\(R=5{\mathrm{[Ω]}}\),コイル\(L=1{\mathrm{[mH]}}\),コンデンサ\(C=10{\mathrm{[μF]}}\)の時の周波数特性
ゲイン\(|G(j{\omega})|\)は入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の比率であり、次式で表されます。
\begin{eqnarray}
|G(j{\omega})|=\left|\frac{V_{OUT}}{V_{IN}}\right|
\end{eqnarray}
また、位相\({\theta}\)は入力電圧\(V_{IN}\)に対する出力電圧\(V_{OUT}\)の位相を示しており、位相\({\theta}\)が『正(プラス)』の場合、『入力電圧\(V_{IN}\)』に対して『出力電圧\(V_{OUT}\)』は位相が進んでいることを示し、位相\({\theta}\)が『負(マイナス)』の場合、『入力電圧\(V_{IN}\)』に対して『出力電圧\(V_{OUT}\)』は位相が遅れていることを示しています。
中心周波数\(f_0\)でゲイン\(|G(j{\omega})|\)が0dB(\(\left|\displaystyle\frac{V_{OUT}}{V_{IN}}\right|=1\))になり、中心周波数\(f_0\)から離れるほどゲイン\(|G(j{\omega})|\)が0dBから小さくなります。
また、赤色と青色の周波数特性を見ると、青色の方がゲイン\(|G(j{\omega})|\)が急峻な特性(周波数fが変化した時において、ゲイン\(|G(j{\omega})|\)の変化が大きい)となっていることが分かります。
上図に示すような、『LC並列共振回路を用いたバンドパスフィルタ』の場合、ゲイン\(|G(j{\omega})|\)の急峻具合を表すパラメータとしてQ値というものがあります。Q値は次式で表され、Q値が高いほど、ゲイン\(|G(j{\omega})|\)が急峻になります。
- 赤色の特性のQ値
- 青色の特性のQ値
\begin{eqnarray}
Q=R\sqrt{\displaystyle\frac{C}{L}}=1×\sqrt{\displaystyle\frac{10×10^{-6}}{1×10^{-3}}}=0.1
\end{eqnarray}
\begin{eqnarray}
Q=R\sqrt{\displaystyle\frac{C}{L}}=5×\sqrt{\displaystyle\frac{10×10^{-6}}{1×10^{-3}}}=0.5
\end{eqnarray}
補足
- Q値は英語では『Quality Factor』と書きます。
- Q値は上図に示すような『LC並列共振回路を用いたバンドパスフィルタ』や『LC直列共振回路を用いたバンドパスフィルタ』でなければ定義することができません。
- 『LC並列共振回路を用いたバンドパスフィルタ』や『LC直列共振回路を用いたバンドパスフィルタ』のような共振回路の場合、信号を通過させる周波数を中心周波数ではなく共振周波数と呼ぶことがあります。一方、共振回路を用いないバンドパスフィルタでは信号を通過させる周波数を中心周波数と呼び、共振周波数という用語を用いません。
『.ac dec 100 10 1000k』は『信号源(ここでは入力電圧\(V_{IN}\))の周波数を10Hz~1000kHzに変化させる。この時、1ディケード(10倍)当たりのステップ数を100とする。』という意味です。
LTspiceでのAC解析の方法は下記の記事で説明していますので、ご参考にしてください。
-



【LTspice】周波数特性を観測する『.ac解析』の使い方と応用
続きを見る
また、LTspiceの『.stepコマンド』については下記の記事で説明していますので、ご参考にしてください。
-


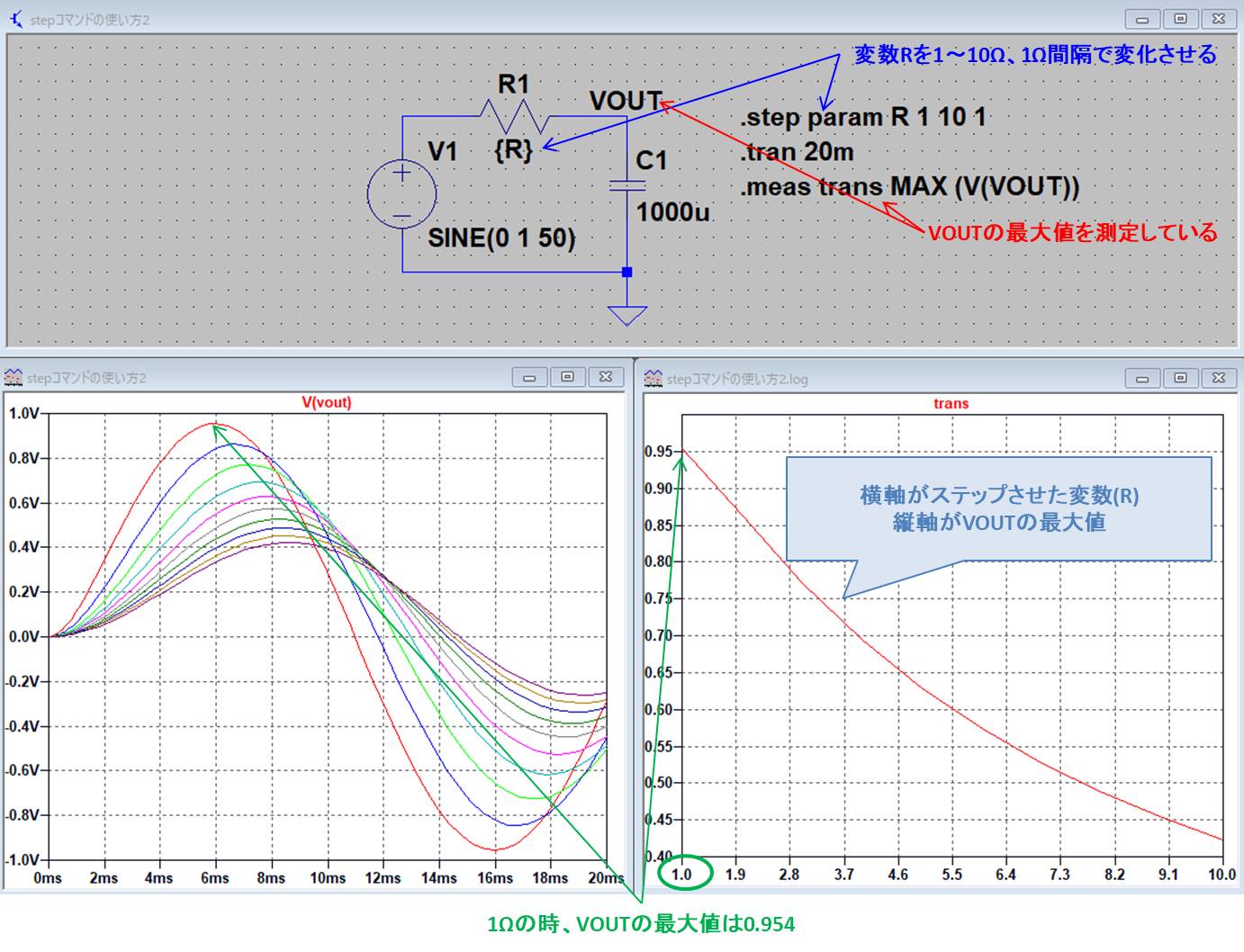
【LTspice】.stepコマンドとは
続きを見る
バンドパスフィルタの『様々な回路』
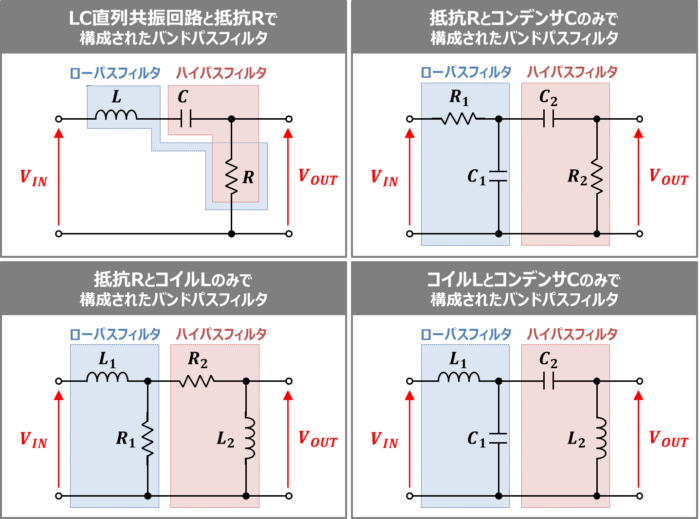

この記事では、一例として『LC並列共振回路と抵抗\(R\)で構成されたバンドパスフィルタ』を取り上げましたが、ローパスフィルタ(LPF)とハイパスフィルタ(HPF)を組み合わせれば、他の回路構成でもバンドパスフィルタを構成することができます。
上図に示している回路は全てバンドパスフィルタです。
- LC直列共振回路と抵抗\(R\)で構成されたバンドパスフィルタ
- 抵抗\(R\)とコンデンサ\(C\)のみで構成されたバンドパスフィルタ
- 抵抗\(R\)とコイル\(L\)のみで構成されたバンドパスフィルタ
- コイル\(L\)とコンデンサ\(C\)のみで構成されたバンドパスフィルタ
→抵抗\(R\)とコイル\(L\)でローパスフィルタを構成しており、抵抗\(R\)とコンデンサ\(C\)でハイパスフィルタを構成している。
→抵抗\(R_1\)とコンデンサ\(C_1\)でローパスフィルタを構成しており、抵抗\(R_2\)とコンデンサ\(C_2\)でハイパスフィルタを構成している。
→コイル\(L_1\)と抵抗\(R_1\)でローパスフィルタを構成しており、コイル\(L_2\)と抵抗\(R_2\)でハイパスフィルタを構成している。
→コイル\(L_1\)とコンデンサ\(C_1\)でローパスフィルタを構成しており、コイル\(L_2\)とコンデンサ\(C_2\)でハイパスフィルタを構成している。
まとめ
この記事では『バンドパスフィルタ』について、以下の内容を説明しました。
- バンドパスフィルタとは
- バンドパスフィルタの『中心周波数』と『カットオフ周波数』
- バンドパスフィルタの『周波数特性』
- バンドパスフィルタの『様々な回路』
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。