この記事では『RCローパスフィルタ』について
- RCローパスフィルタとは
- RCローパスフィルタの『伝達関数』,『ゲイン』,『カットオフ周波数』,『位相』
- RCローパスフィルタの『周波数特性』
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
RCローパスフィルタとは
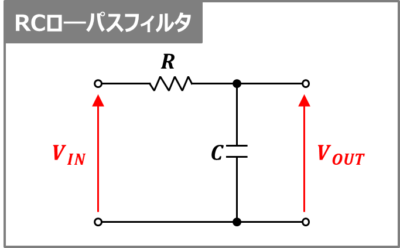
上図にRCローパスフィルタの回路構成を示しています。
RCローパスフィルタは、抵抗\(R\)とコンデンサ\(C\)のみで構成された最も簡単なローパスフィルタです。入力電圧\(V_{IN}\)の低周波成分を通過させ、高周波成分を遮断します。
後ほど導出方法など詳細に説明しますが、RCローパスフィルタの『伝達関数』,『ゲイン』,『カットオフ周波数』,『位相』の式と『周波数特性』をまとめると、下記のようになります。
RCローパスフィルタのまとめ
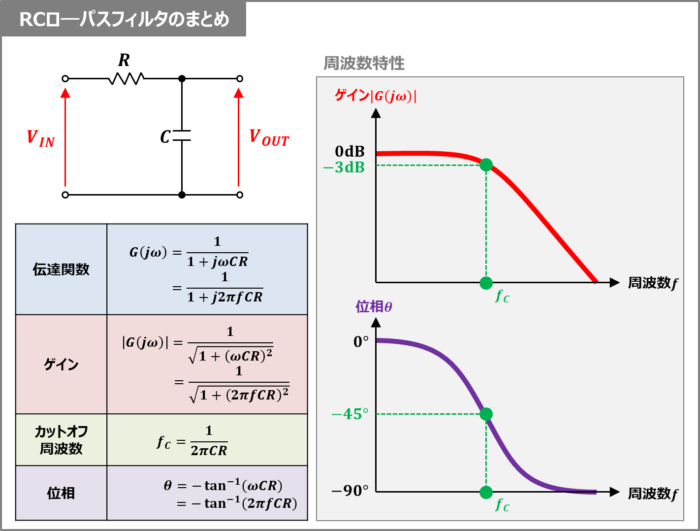
- 伝達関数\(G(j{\omega})\)
- ゲイン\(|G(j{\omega})|\)
- カットオフ周波数\(f_C\)
- 位相\({\theta}\)
→入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の比が伝達関数\(G(j{\omega})\)であり、次式となる。
\begin{eqnarray}
G(j{\omega})=\frac{V_{OUT}}{V_{IN}}=\frac{1}{1+j{\omega}CR}=\frac{1}{1+j2{\pi}fCR}\tag{1-1}
\end{eqnarray}
→伝達関数\(G(j{\omega})\)の絶対値がゲイン\(|G(j{\omega})|\)であり、次式となる。
\begin{eqnarray}
|G(j{\omega})|=\frac{1}{\sqrt{1+({\omega}CR)^2}}=\frac{1}{\sqrt{1+(2{\pi}fCR)^2}}\tag{1-2}
\end{eqnarray}
→ゲイン\(|G(j{\omega})|\)が\(\displaystyle\frac{1}{\sqrt{2}}({\;}{\approx}{\;}0.707)\)になる周波数がカットオフ周波数\(f_C\)であり、次式となる。
\begin{eqnarray}
f_C=\frac{1}{2{\pi}CR}\tag{1-3}
\end{eqnarray}
→入力電圧\(V_{IN}\)に対する出力電圧\(V_{OUT}\)の位相であり、次式となる。
\begin{eqnarray}
{\theta}=-{\tan}^{-1}({\omega}CR)=-{\tan}^{-1}(2{\pi}fCR)\tag{1-4}
\end{eqnarray}
入力電圧\(V_{IN}\)の周波数が高い場合、コンデンサ\(C\)のインピーダンスが小さいので、出力電圧\(V_{OUT}\)が低くなる(すなわち、高周波成分を遮断する)ということは見当がつくと思います。
補足
- ローパスフィルタは『低域通過フィルタ』や『ハイカットフィルタ』とも呼ばれています。
RCローパスフィルタの『伝達関数』と『ゲイン』
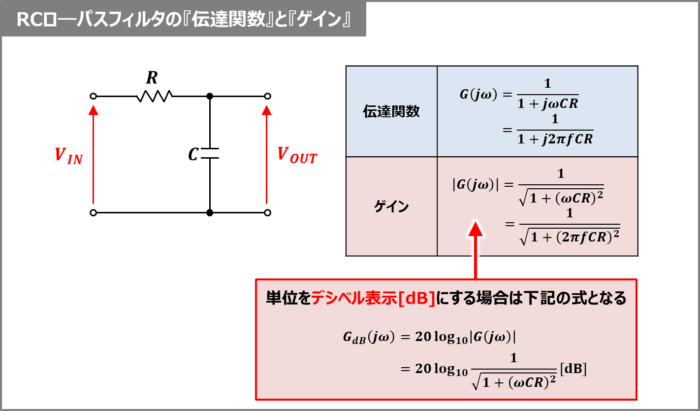
RCローパスフィルタの『伝達関数』と『ゲイン』の導出方法について説明します。
『抵抗\(R\)のインピーダンス\({\dot{Z}_R}\)』と『コンデンサ\(C\)のインピーダンス\({\dot{Z}_C}\)』は次式で表されます。
\begin{eqnarray}
{\dot{Z}_R}&=&R\tag{2-1}\\
\\
{\dot{Z}_C}&=&\frac{1}{j{\omega}C}\tag{2-2}
\end{eqnarray}
したがって、出力電圧\(V_{OUT}\)は入力電圧\(V_{IN}\)を\({\dot{Z}_R}\)と\({\dot{Z}_C}\)で分圧しているので、次式で表されます。
\begin{eqnarray}
V_{OUT}=\displaystyle\frac{{\dot{Z}_C}}{{\dot{Z}_R}+{\dot{Z}_C}}V_{IN}=\frac{\displaystyle\frac{1}{j{\omega}C}}{R+\displaystyle\frac{1}{j{\omega}C}}V_{IN}=\frac{1}{1+j{\omega}CR}V_{IN}\tag{2-3}
\end{eqnarray}
RCローパスフィルタの伝達関数\(G(j{\omega})\)は入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の比です。そのため、(2-3)式を変形すると、伝達関数\(G(j{\omega})\)は次式で表すことができます。
\begin{eqnarray}
G(j{\omega})=\frac{V_{OUT}}{V_{IN}}=\frac{1}{1+j{\omega}CR}\tag{2-4}
\end{eqnarray}
(2-4)式の分母には虚数単位\(j\)があります。ここで分子のみに虚数単位\(j\)がくるようにするために、分母と分子に『\(1-j{\omega}CR\)』を掛けます。すると(2-4)式は次式に変形することができます。
\begin{eqnarray}
G(j{\omega})=\frac{1}{1+j{\omega}CR}×\frac{1-j{\omega}CR}{1-j{\omega}CR}=\frac{1}{1+({\omega}CR)^2}-j\frac{{\omega}CR}{1+({\omega}CR)^2}\tag{2-5}
\end{eqnarray}
伝達関数\(G(j{\omega})\)の絶対値がRCローパスフィルタのゲイン\(|G(j{\omega})|\)となります。もう少し詳しく説明すると、RCローパスフィルタのゲイン\(|G(j{\omega})|\)は(2-5)式において、『実部\(\left\{\displaystyle\frac{1}{1+({\omega}CR)^2}\right\}\)の2乗』と『虚部\(\left\{\displaystyle\frac{-{\omega}CR}{1+({\omega}CR)^2}\right\}\)の2乗』を足して、平方根を取ることで求めることができます。そのため、ゲイン\(|G(j{\omega})|\)は次式となります。
\begin{eqnarray}
|G(j{\omega})|&=&\sqrt{\left\{\frac{1}{1+({\omega}CR)^2}\right\}^2+\left\{\frac{-{\omega}CR}{1+({\omega}CR)^2}\right\}^2}\\
\\
&=&\sqrt{\frac{1+({\omega}CR)^2}{\left\{1+({\omega}CR)^2\right\}^2}}\\
\\
&=&\sqrt{\frac{1}{1+({\omega}CR)^2}}\\
\\
&=&\frac{1}{\sqrt{1+({\omega}CR)^2}}\tag{2-6}
\end{eqnarray}
ここで、角周波数\({\omega}\)は\({\omega}=2{\pi}f\)の関係があるので、(2-6)式の\({\omega}\)を\(2{\pi}f\)に書き換えると、次式となります。
\begin{eqnarray}
|G(j{\omega})|=\frac{1}{\sqrt{1+(2{\pi}fCR)^2}}\tag{2-7}
\end{eqnarray}
なお、RCローパスフィルタのゲイン\(|G(j{\omega})|\)をデシベル表示にしたものを\(G_{dB}(j{\omega})\)とすると、\(G_{dB}(j{\omega})\)は次式となります。
\begin{eqnarray}
G_{dB}(j{\omega})&=&20{\log}_{10}|G(j{\omega})|\\
\\
&=&20{\log}_{10}\frac{1}{\sqrt{1+({\omega}CR)^2}}{\mathrm{[dB]}}\\
\\
&=&20{\log}_{10}\frac{1}{\sqrt{1+(2{\pi}fCR)^2}}{\mathrm{[dB]}}\tag{2-8}
\end{eqnarray}
これで、RCローパスフィルタの『伝達関数』と『ゲイン』の導出は終わりです。
『ラプラス演算子\(s=j{\omega}\)』と『RCローパスフィルタの時定数\({\tau}=RC\)』を用いると、伝達関数\(G(j{\omega})\)は次式となります。
\begin{eqnarray}
G(j{\omega})=\frac{1}{1+j{\omega}CR}=\frac{1}{1+s{\tau}}
\end{eqnarray}
伝達関数\(G(j{\omega})\)を上式で表している資料もよく見かけます。なお、分母の『ラプラス演算子\(s\)』の次数が1次なので、1次ローパスフィルタとなります。
あわせて読みたい
(2-8)式に示すように、ゲイン\(|G(j{\omega})|\)をデシベルで表す場合には、ゲインの常用対数(\({\log}_{10}\))を20倍します。デシベルについて詳しくは下記の記事で説明していますので、ご参考になれば幸いです。
-

電圧や電力の『デシベル(dB)』とは?計算方法や変換方法について
続きを見る
RCローパスフィルタの『カットオフ周波数』
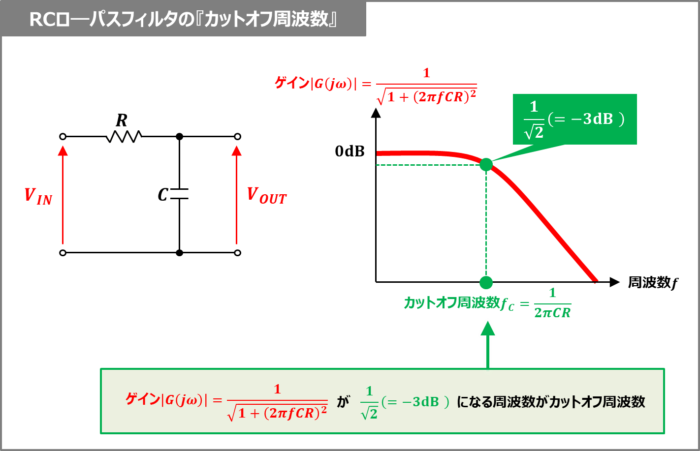

カットオフ周波数\(f_C\)は、RCローパスフィルタのゲイン\(|G(j{\omega})|\)が\(\displaystyle\frac{1}{\sqrt{2}}({\;}{\approx}{\;}0.707)\)になる周波数であり、次式となります。
\begin{eqnarray}
\frac{1}{\sqrt{2}}&=&|G(j{\omega})|\\
\\
&=&\frac{1}{\sqrt{1+(2{\pi}f_CCR)^2}}\\
\\
{\Leftrightarrow}\sqrt{1+(2{\pi}f_CCR)^2}&=&\sqrt{2}\\
\\
1+(2{\pi}f_CCR)^2&=&2\\
\\
(2{\pi}f_CCR)^2&=&1\\
\\
2{\pi}f_CCR&=&1\\
\\
f_C&=&\frac{1}{2{\pi}CR}\tag{3-1}
\end{eqnarray}
入力電圧\(V_{IN}\)はRCローパスフィルタによって、カットオフ周波数\(f_C\)より低い成分の周波数はほとんど通過し、カットオフ周波数\(f_C\)より高い成分の周波数は減衰します。
あわせて読みたい
『カットオフ周波数って何?』『何でゲイン\(|G(j{\omega})|\)が\(\displaystyle\frac{1}{\sqrt{2}}({\;}{\approx}{\;}0.707)\)になる周波数がカットオフ周波数なの?』という方は下記の記事が役に立つと思いますので、ご参考にしてください。
-


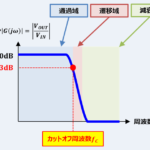
『カットオフ周波数(遮断周波数)』とは?【フィルタ回路】
続きを見る
RCローパスフィルタの時定数\({\tau}\)は『\({\tau}=RC\)』なので、(3-1)式の\(RC\)を\({\tau}\)に置き換えると次式となります。
\begin{eqnarray}
f_C=\frac{1}{2{\pi}CR}=\frac{1}{2{\pi}{\tau}}\tag{3-2}
\end{eqnarray}
つまり、カットオフ周波数\(f_C\)は時定数\({\tau}\)に反比例します。抵抗の抵抗値\(R\)が大きいほど、コンデンサの静電容量\(C\)が大きいほど、カットオフ周波数\(f_C\)は低くなります。
補足
- RCローパスフィルタのゲイン\(|G(j{\omega})|\)が\(\displaystyle\frac{1}{\sqrt{2}}({\;}{\approx}{\;}0.707)\)になる時は、デシベル単位で表すと次式に示すように約-3dBとなります。
\begin{eqnarray}
G_{dB}(j{\omega})&=&20{\log}_{10}\frac{1}{\sqrt{2}}\\
\\
&=&-3.01029{\cdots}{\mathrm{[dB]}}\\
\\
&{\approx}&-3{\mathrm{[dB]}}
\end{eqnarray} - カットオフ周波数は『遮断周波数』とも呼ばれています。
『カットオフ角周波数』について
カットオフ角周波数\({\omega}_C\)は次式となります。
\begin{eqnarray}
{\omega}_C=\frac{1}{CR}
\end{eqnarray}
上式を用いると、伝達関数\(G(j{\omega})\)とゲイン\(|G(j{\omega})|\)は次式となります。
\begin{eqnarray}
G(j{\omega})&=&\frac{1}{1+j{\omega}CR}=\frac{1}{1+j\displaystyle\frac{{\omega}}{{\omega}_C}}\\
\\
|G(j{\omega})|&=&\frac{1}{\sqrt{1+({\omega}CR)^2}}=\frac{1}{\sqrt{1+\left(\displaystyle\frac{{\omega}}{{\omega}_C}\right)^2}}
\end{eqnarray}
伝達関数\(G(j{\omega})\)とゲイン\(|G(j{\omega})|\)を上式で表している資料もよく見かけます。
RCローパスフィルタの『位相』
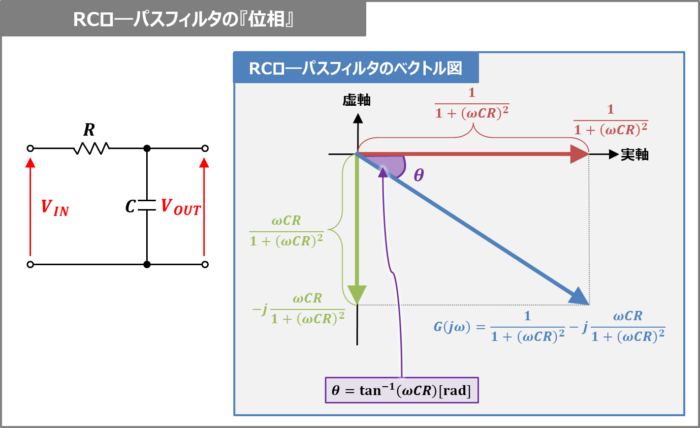

繰り返しになりますが、RCローパスフィルタの伝達関数\(G(j{\omega})\)は次式で表されます。
\begin{eqnarray}
G(j{\omega})=\frac{1}{1+({\omega}CR)^2}-j\frac{{\omega}CR}{1+({\omega}CR)^2}\tag{4-1}
\end{eqnarray}
複素平面(横軸は実数の目盛、縦軸は虚数の目盛であり、ガウス平面とも呼ばれている)上に(4-1)式のベクトルを描くと上図のようになります。このベクトル図よりRCローパスフィルタの位相\({\theta}\)を求めることができ、次式で表されます。
\begin{eqnarray}
{\tan}{\theta}&=&\frac{\displaystyle\frac{-{\omega}CR}{1+({\omega}CR)^2}}{\displaystyle\frac{1}{1+({\omega}CR)^2}}\\
\\
&=&-{\omega}CR\\
\\
{\Leftrightarrow}{\theta}&=&{\tan}^{-1}(-{\omega}CR)\\
\\
&=&-{\tan}^{-1}({\omega}CR)\\
\\
&=&-{\tan}^{-1}(2{\pi}fCR)\tag{4-2}
\end{eqnarray}
なお、カットオフ周波数\(f_C\)における位相\({\theta}_C\)は以下の値となります。
\begin{eqnarray}
{\theta}_C&=&-{\tan}^{-1}(2{\pi}f_CCR)\\
\\
&=&-{\tan}^{-1}(2{\pi}×\frac{1}{2{\pi}CR}×CR)\\
\\
&=&-{\tan}^{-1}(1)\\
\\
&=&-0.7853{\cdots}{\mathrm{[rad]}}\tag{4-3}
\end{eqnarray}
上式の単位は[rad](ラジアン)なので、[rad]を[°(度)]に変換すると、次式に示すように-45°(度)となります。
\begin{eqnarray}
{\theta}_C&=&-{\tan}^{-1}(1)×\frac{180}{{\pi}}\\
\\
&=&-45{\mathrm{°}}\tag{4-4}
\end{eqnarray}
[rad]を[°(度)]に変換するためには、\(\displaystyle\frac{180}{{\pi}}\)を掛けます。
RCローパスフィルタの『周波数特性』
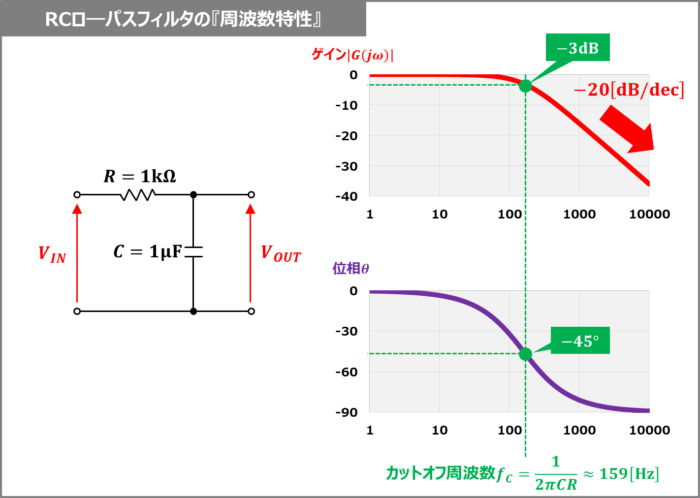

一例として、抵抗\(R=1{\mathrm{[kΩ]}}\)、コンデンサ\(C=1{\mathrm{[μF]}}\)のRCローパスフィルタにおいて、ゲイン\(|G(j{\omega})|\)と位相\({\theta}\)の周波数特性を上図に示しています。
RCローパスフィルタのカットオフ周波数\(f_C\)は以下の値となります。
\begin{eqnarray}
f_C&=&\frac{1}{2{\pi}CR}\\
\\
&=&\frac{1}{2{\pi}×1×10^{-6}×1×10^{3}}\\
\\
&=&159.154{\cdots}\\
\\
&{\approx}&159{\mathrm{[Hz]}}\tag{5-1}
\end{eqnarray}
上図を見ると、カットオフ周波数\(f_C{\;}{\approx}{\;}159{\mathrm{[Hz]}}\)でゲイン\(|G(j{\omega})|\)が約-3dB、位相\({\theta}\)が-45°になっていることが確認できます。
また、周波数\(f\)が高くて『\(1{\;}{\ll}{\;}(2{\pi}fCR)^2\)』とみなせる場合、『1』を無視すると、ゲイン\(|G(j{\omega})|\)は次式で表すことができます。
\begin{eqnarray}
|G(j{\omega})|&=&\frac{1}{\sqrt{1+(2{\pi}fCR)^2}}\\
\\
&{\approx}&\frac{1}{\sqrt{(2{\pi}fCR)^2}}\\
\\
&{\approx}&\frac{1}{2{\pi}fCR}\tag{5-2}\\
\end{eqnarray}
上式より、周波数\(f\)が10倍になると、ゲイン\(|G(j{\omega})|\)が1/10になります(デシベル表記では、『\(G_{dB}(j{\omega})=20{\log}_{10}\displaystyle\frac{1}{10}=-20{\mathrm{[dB]}}\)』となります)。つまり、周波数が高い領域では、-20[dB/dec]の傾きでゲイン\(|G(j{\omega})|\)が減少しています。
同様に、周波数fが2倍になると、ゲイン\(|G(j{\omega})|\)が1/2になります(デシベル表記では、『\(G_{dB}(j{\omega})=20{\log}_{10}\displaystyle\frac{1}{2}=-6{\mathrm{[dB]}}\)』となります)。つまり、周波数が高い領域では、-6[dB/oct]の傾きでゲイン\(|G(j{\omega})|\)が減少しているとも言います。
周波数fが2倍になることをoct(オクターブ)、10倍になることをdec(ディケード)といいます。
RCローパスフィルタの『周波数特性』をLTspiceで描く方法
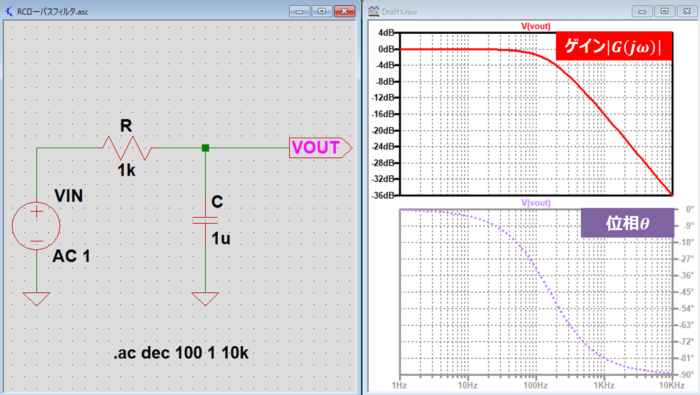

『周波数特性』をLTspiceで描くためには『.ac解析』を用います。
上図にLTspiceで描いたRCローパスフィルタを示しています(\(R=1{\mathrm{[kΩ]}}\)、\(C=1{\mathrm{[μF]}}\))。
VOUT端子の電圧をプロットすることで、周波数特性を出力することができるようになります。
『.ac dec 100 1 10k』は『信号源(ここでは入力電圧\(V_{IN}\))の周波数を1Hz~10kHzに変化させる。この時、1ディケード(10倍)当たりのステップ数を100とする。』という意味です。
LTspiceでのAC解析の方法は下記の記事で説明していますので、ご参考にしてください。
-



【LTspice】周波数特性を観測する『.ac解析』の使い方と応用
続きを見る
まとめ
この記事では『RCローパスフィルタ』について、以下の内容を説明しました。
- RCローパスフィルタとは
- RCローパスフィルタの『伝達関数』,『ゲイン』,『カットオフ周波数』,『位相』
- RCローパスフィルタの『周波数特性』
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。







