『カットオフ周波数(遮断周波数)』とは？【フィルタ回路】

この記事では、フィルタ回路において重要な用語である『カットオフ周波数(遮断周波数)』について

『カットオフ周波数』とは
『カットオフ周波数』の時の電力と電圧
『カットオフ周波数』をシミュレーションで確かめてみる

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

『カットオフ周波数』とは

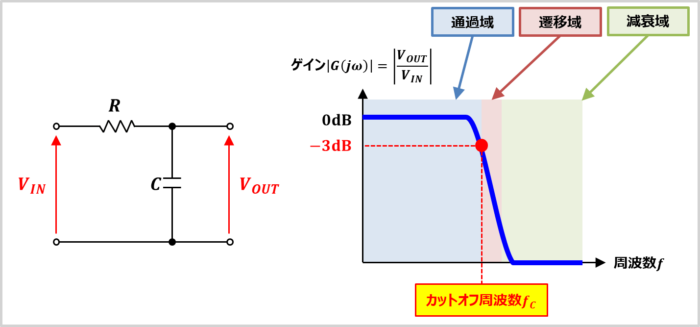
カットオフ周波数とは、フィルタ回路において、通過域と遷移域の境界となる周波数です。

上図にRCローパスフィルタを一例として、横軸を周波数\(f\)、縦軸をゲイン\(|G(j{\omega})|\)としたグラフを示します。縦軸のゲイン\(|G(j{\omega})|\)は入力電圧\(V_{IN}\)に対する出力電圧\(V_{OUT}\)の電圧比であり、次式で表されます。

\begin{eqnarray}
|G(j{\omega})|=\left|\frac{V_{OUT}}{V_{IN}}\right|
\end{eqnarray}

ゲイン\(|G(j{\omega})|\)をデシベル[dB]で表す場合には、ゲインの常用対数(\({\log}_{10}\))を20倍します。したがって、次式に示すように、入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)が等しくなるときは0dBとなります。

\begin{eqnarray}
20{\log}_{10}|G(j{\omega})|=20{\log}_{10}\left|\frac{V_{OUT}}{V_{IN}}\right|=20{\log}_{10}1=0{\mathrm{[dB]}}
\end{eqnarray}

入力電圧\(V_{IN}\)の周波数\(f\)が高くなると、コンデンサ\(C\)のインピーダンスが小さくなり、出力電圧\(V_{OUT}\)が低くなる(すなわち、ゲイン\(|G(j{\omega})|\)が低下する)ということは見当がつくと思います。

ここで、通過域とは、入力電圧\(V_{IN}\)が減衰せずに通過する周波数帯域のことを示しています。また、減衰域とは、入力電圧\(V_{IN}\)を減衰させる周波数帯域のことを示しています。この通過域と減衰域の中間が遷移域となります。通過域と遷移域の境界がカットオフ周波数となります。

『カットオフ周波数』の時の電力と電圧

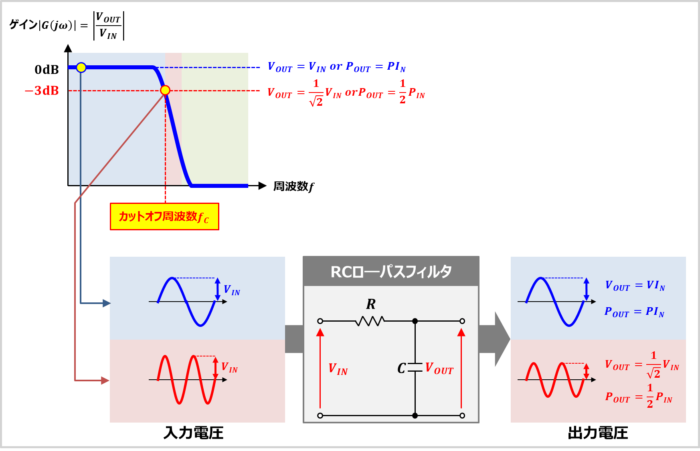
通過域と遷移域の境目であるカットオフ周波数\(f_C\)では、ゲイン\(|G(j{\omega})|\)が通過域平坦部から3dB低下しています。

カットオフ周波数\(f_C\)では、電力は通過域平坦部の\(\displaystyle\frac{1}{2}倍\)となります。一方、電圧は通過域平坦部の\(\displaystyle\frac{1}{\sqrt{2}}=約0.707倍\)となります。

カットオフ周波数\(f_C\)は言い換えれば、『入力電圧\(V_{IN}\)がフィルタを通過する電力(エネルギー)』と『入力電圧\(V_{IN}\)がフィルタによって減衰される電力(エネルギー)』の境目となります。

『入力電圧\(V_{IN}\)の周波数\(f\)』が『フィルタ回路のカットオフ周波数\(f_C\)』と等しい時には、半分の電力(エネルギー)しかフィルタ回路を通過することができないのです。

RCローパスフィルタの『カットオフ周波数』を導出してみる

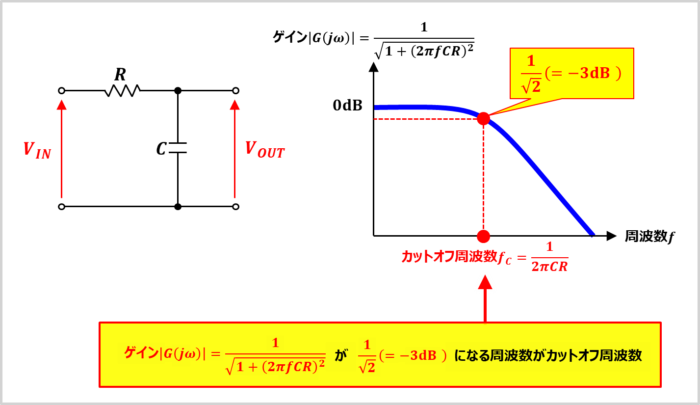
一例として、RCローパスフィルタの『カットオフ周波数』の導出方法について説明します。

『抵抗\(R\)のインピーダンス\({\dot{Z}_R}\)』と『コンデンサ\(C\)のインピーダンス\({\dot{Z}_C}\)』は次式で表されます。

\begin{eqnarray}
{\dot{Z}_R}&=&R\tag{1-1}\\
\\
{\dot{Z}_C}&=&\frac{1}{j{\omega}C}\tag{1-2}
\end{eqnarray}

出力電圧\(V_{OUT}\)は入力電圧\(V_{IN}\)を\({\dot{Z}_R}\)と\({\dot{Z}_C}\)で分圧しているので、次式で表されます。

\begin{eqnarray}
V_{OUT}=\displaystyle\frac{{\dot{Z}_C}}{{\dot{Z}_R}+{\dot{Z}_C}}V_{IN}=\frac{\displaystyle\frac{1}{j{\omega}C}}{R+\displaystyle\frac{1}{j{\omega}C}}V_{IN}=\frac{1}{1+j{\omega}CR}V_{IN}\tag{1-3}
\end{eqnarray}

RCローパスフィルタの伝達関数\(G(j{\omega})\)は入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の比です。そのため、(1-3)式を変形すると、伝達関数\(G(j{\omega})\)は次式で表すことができます。

\begin{eqnarray}
G(j{\omega})=\frac{V_{OUT}}{V_{IN}}=\frac{1}{1+j{\omega}CR}\tag{1-4}
\end{eqnarray}

(1-4)式の分母には虚数単位\(j\)があります。ここで分子のみに虚数単位\(j\)がくるようにするために、分母と分子に『\(1-j{\omega}CR\)』を掛けます。すると(1-4)式は次式に変形することができます。

\begin{eqnarray}
G(j{\omega})=\frac{1}{1+j{\omega}CR}×\frac{1-j{\omega}CR}{1-j{\omega}CR}=\frac{1}{1+({\omega}CR)^2}-j\frac{{\omega}CR}{1+({\omega}CR)^2}\tag{1-5}
\end{eqnarray}

伝達関数\(G(j{\omega})\)の絶対値がRCローパスフィルタのゲイン\(|G(j{\omega})|\)となります。もう少し詳しく説明すると、RCローパスフィルタのゲイン\(|G(j{\omega})|\)は(2-5)式において、『実部\(\left\{\displaystyle\frac{1}{1+({\omega}CR)^2}\right\}\)の2乗』と『虚部\(\left\{\displaystyle\frac{-{\omega}CR}{1+({\omega}CR)^2}\right\}\)の2乗』を足して、平方根を取ることで求めることができます。そのため、ゲイン\(|G(j{\omega})|\)は次式となります。

\begin{eqnarray}
|G(j{\omega})|&=&\sqrt{\left\{\frac{1}{1+({\omega}CR)^2}\right\}^2+\left\{\frac{-{\omega}CR}{1+({\omega}CR)^2}\right\}^2}\\
\\
&=&\sqrt{\frac{1+({\omega}CR)^2}{\left\{1+({\omega}CR)^2\right\}^2}}\\
\\
&=&\sqrt{\frac{1}{1+({\omega}CR)^2}}\\
\\
&=&\frac{1}{\sqrt{1+({\omega}CR)^2}}\tag{1-6}
\end{eqnarray}

ここで、角周波数\({\omega}\)は\({\omega}=2{\pi}f\)の関係があるので、(2-6)式の\({\omega}\)を\(2{\pi}f\)に書き換えると、次式となります。

\begin{eqnarray}
|G(j{\omega})|=\frac{1}{\sqrt{1+(2{\pi}fCR)^2}}\tag{1-7}
\end{eqnarray}

カットオフ周波数\(f_C\)は、RCローパスフィルタのゲイン\(|G(j{\omega})|\)が\(\displaystyle\frac{1}{\sqrt{2}}({\;}{\approx}{\;}0.707)\)になる周波数であり、次式となります。

\begin{eqnarray}
\frac{1}{\sqrt{2}}&=&|G(j{\omega})|\\
\\
&=&\frac{1}{\sqrt{1+(2{\pi}f_CCR)^2}}\\
\\
{\Leftrightarrow}\sqrt{1+(2{\pi}f_CCR)^2}&=&\sqrt{2}\\
\\
1+(2{\pi}f_CCR)^2&=&2\\
\\
(2{\pi}f_CCR)^2&=&1\\
\\
2{\pi}f_CCR&=&1\\
\\
f_C&=&\frac{1}{2{\pi}CR}\tag{1-8}
\end{eqnarray}

RCローパスフィルタの時定数\({\tau}\)は『\({\tau}=RC\)』なので、(1-8)式の\(RC\)を\({\tau}\)に置き換えると次式となります。

\begin{eqnarray}
f_C=\frac{1}{2{\pi}CR}=\frac{1}{2{\pi}{\tau}}\tag{1-9}
\end{eqnarray}

つまり、カットオフ周波数\(f_C\)は時定数\({\tau}\)に反比例します。抵抗の抵抗値\(R\)が大きいほど、コンデンサの静電容量\(C\)が大きいほど、カットオフ周波数\(f_C\)は低くなります。

カットオフ周波数をシミュレーションで確かめてみる

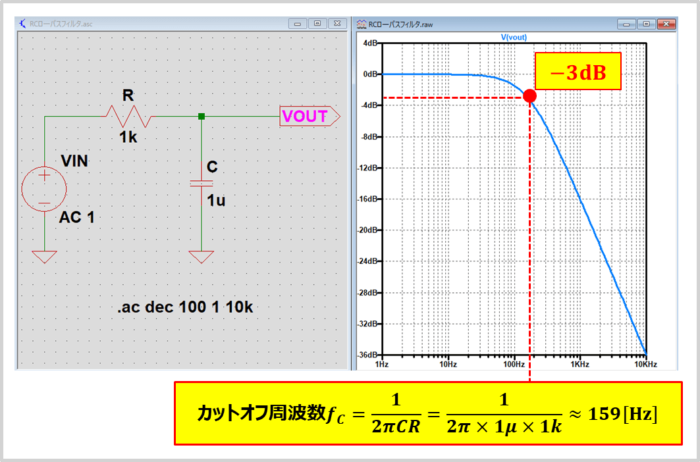
抵抗\(R=1{\mathrm{[kΩ]}}\)、コンデンサ\(C=1{\mathrm{[μF]}}\)において、RCローパスフィルタのシミュレーションをLTspiceで行ってみます。『周波数特性』をLTspiceで描くためには『AC解析』を用います。

RCローパスフィルタのカットオフ周波数\(f_C\)は以下の値となります。

\begin{eqnarray}
f_C&=&\frac{1}{2{\pi}CR}\\
\\
&=&\frac{1}{2{\pi}×1×10^{-6}×1×10^{3}}\\
\\
&=&159.154{\cdots}\\
\\
&{\approx}&159{\mathrm{[Hz]}}\tag{5-1}
\end{eqnarray}

シミュレーション結果を見ると、カットオフ周波数\(f_C{\;}{\approx}{\;}159{\mathrm{[Hz]}}\)でゲイン\(|G(j{\omega})|\)が約－3dBになっていることが確認できます。

『.ac dec 100 1 10k』は『信号源(ここでは入力電圧\(V_{IN}\))の周波数を1Hz～10kHzに変化させる。この時、1ディケード(10倍)当たりのステップ数を100とする。』という意味です。

LTspiceでのAC解析の方法は下記の記事で説明していますので、ご参考にしてください。