直列接続しているコンデンサにかかる電圧は？【分圧】

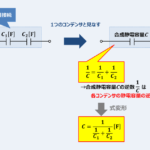
この記事では『直列接続しているコンデンサ』について

直列接続しているコンデンサにかかる電圧の『計算方法』・『証明』・『例題』

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

直列接続しているコンデンサにかかる電圧

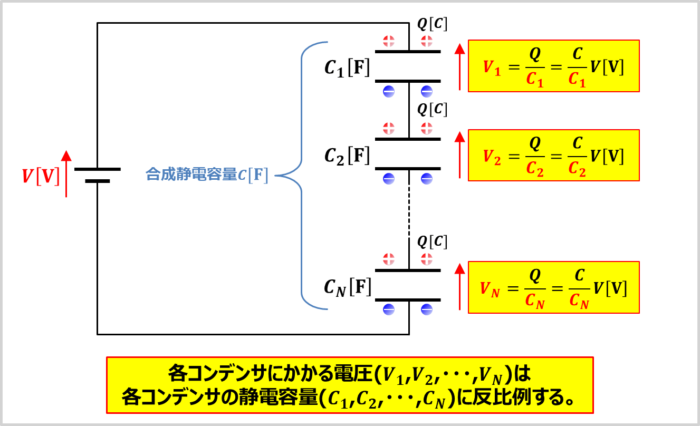
上図に、直列接続されているNつのコンデンサ(各コンデンサの静電容量を\(C_1{\mathrm{[F]}}\),\(C_2{\mathrm{[F]}}\),・・・,\(C_N{\mathrm{[F]}}\)とする)と電源電圧\(V{\mathrm{[V]}}\)を接続している回路を示しています。

この回路において、各コンデンサに蓄えられる電荷を\(Q{\mathrm{[C]}}\)、Nつのコンデンサの合成静電容量を\(C{\mathrm{[F]}}\)とすると、各コンデンサにかかる電圧(\(V_1{\mathrm{[V]}}\),\(V_2{\mathrm{[V]}}\),・・・,\(V_N{\mathrm{[V]}}\))は次式で求めることができます。

コンデンサ\(C_1\)にかかる電圧\(V_1{\mathrm{[V]}}\)

\begin{eqnarray}
V_1&=&\frac{Q}{C_1}=\frac{C}{C_1}×V{\mathrm{[V]}}\tag{1}
\end{eqnarray}

コンデンサ\(C_2\)にかかる電圧\(V_2{\mathrm{[V]}}\)

\begin{eqnarray}
V_2&=&\frac{Q}{C_2}=\frac{C}{C_2}×V{\mathrm{[V]}}\tag{2}
\end{eqnarray}

コンデンサ\(C_N\)にかかる電圧\(V_N{\mathrm{[V]}}\)

\begin{eqnarray}
V_N&=&\frac{Q}{C_N}=\frac{C}{C_N}×V{\mathrm{[V]}}\tag{3}
\end{eqnarray}

上式から分かるように、各コンデンサにかかる電圧(\(V_1\),\(V_2\),・・・,\(V_N\))は各コンデンサの静電容量(\(C_1\),\(C_2\),・・・,\(C_N\))に反比例します。

コンデンサの直列接続と電荷

コンデンサを直列接続した場合、静電容量の大きさに関わらず、各コンデンサに蓄えられている電荷が同じとなります。

直列接続しているコンデンサにかかる電圧の『証明』

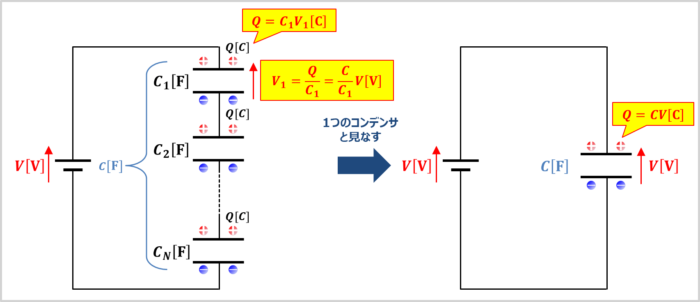
直列接続されているNつのコンデンサ(各コンデンサの静電容量を\(C_1{\mathrm{[F]}}\),\(C_2{\mathrm{[F]}}\),・・・,\(C_N{\mathrm{[F]}}\)とする)を1つと見なした時の合成静電容量を\(C{\mathrm{[F]}}\)とします。

また、直列接続されているNつのコンデンサを1つと見なした時のコンデンサに蓄えられる電荷を\(Q{\mathrm{[C]}}\)とすると、次式が成り立ちます。

\begin{eqnarray}
Q=CV\tag{4}
\end{eqnarray}

また、コンデンサが直列接続されている時、静電容量の大きさに関わらず、各コンデンサに蓄えられている電荷が同じになります(「直列接続されているNつのコンデンサを1つと見なした時に蓄えられる電荷」と「各コンデンサ\(C_1\),\(C_2\),・・・,\(C_N\)に蓄えられる電荷」が同じということ)。

したがって、コンデンサ\(C_1\)にかかる電圧\(V_1{\mathrm{[V]}}\)は次式で表すことができます。

\begin{eqnarray}
Q&=&C_1V_1\\
\\
{\Leftrightarrow}V_1&=&\frac{Q}{C_1}{\mathrm{[V]}}\tag{5}
\end{eqnarray}

(4)式を(5)式に代入すると、次式となり、(1)式が成り立つことが分かります。

\begin{eqnarray}
V_1&=&\frac{Q}{C_1}=\frac{C}{C_1}×V{\mathrm{[V]}}\tag{6}
\end{eqnarray}

直列接続しているコンデンサにかかる電圧の『例題』

例題

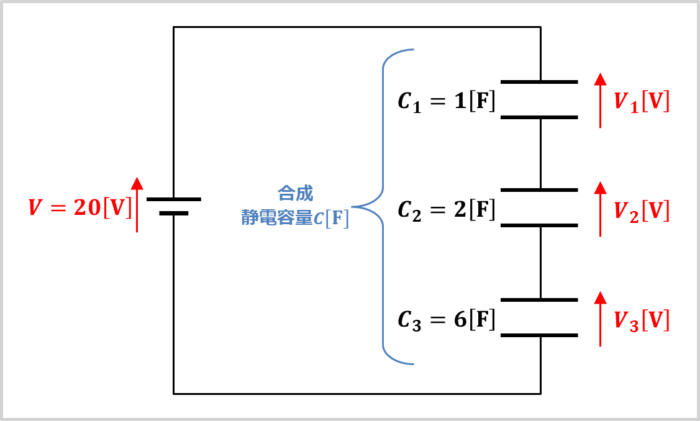
上図に、直列接続されている3つのコンデンサ\(C_1\)～\(C_3\)と電源電圧\(V\)を接続している回路を示しています。

この回路において、コンデンサ\(C_1\)～\(C_3\)の静電容量と電源電圧\(V\)が以下の値の時、

\begin{eqnarray}
C_1&=&1{\mathrm{[F]}}\\
C_2&=&2{\mathrm{[F]}}\\
C_3&=&6{\mathrm{[F]}}\\
V&=&20{\mathrm{[V]}}
\end{eqnarray}

コンデンサ\(C_1\)～\(C_3\)にかかる電圧は何\(\mathrm{V}\)になるでしょうか。

解答

3つのコンデンサ\(C_1\)～\(C_3\)を1つと見なした時の合成静電容量\(C\)は以下の値となります。

\begin{eqnarray}
C&=&\frac{1}{\displaystyle\frac{1}{C_1}+\displaystyle\frac{1}{C_2}+\displaystyle\frac{1}{C_3}}\\
\\
&=&\frac{1}{\displaystyle\frac{1}{1}+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{6}}\\
\\
&=&\frac{6}{\displaystyle\frac{6}{1}+\displaystyle\frac{6}{2}+\displaystyle\frac{6}{6}}\\
\\
&=&\frac{6}{6+3+1}\\
\\
&=&\frac{6}{10}{\mathrm{[F]}}\tag{7}
\end{eqnarray}

直列接続されているNつのコンデンサを1つと見なした時のコンデンサに蓄えられる電荷を\(Q{\mathrm{[C]}}\)とすると、次式が成り立ちます。

\begin{eqnarray}
Q=CV=\frac{6}{10}×20=12{\mathrm{[C]}}\tag{8}
\end{eqnarray}

コンデンサが直列接続されている時、静電容量の大きさに関わらず、各コンデンサに蓄えられている電荷が同じになるため、各コンデンサ\(C_1\)～\(C_3\)にかかる電圧\(V_1\)～\(V_3\)は以下の値となります。

\begin{eqnarray}
V_1&=&\frac{Q}{C_1}=\frac{12}{1}=12{\mathrm{[V]}}\tag{9}\\
\\
V_2&=&\frac{Q}{C_2}=\frac{12}{2}=6{\mathrm{[V]}}\tag{10}\\
\\
V_3&=&\frac{Q}{C_3}=\frac{12}{6}=2{\mathrm{[V]}}\tag{11}
\end{eqnarray}

各コンデンサにかかる電圧はコンデンサの静電容量に反比例するので、静電容量の小さいコンデンサ\(C_1\)には大きな電圧が印加され、静電容量が大きなコンデンサ\(C_3\)には小さな電圧が印加されるということになります。

【補足】直列接続しているコンデンサに流れる電流

コンデンサが直列接続されている時、各コンデンサに流れる電流は、コンデンサの静電容量とは無関係で全て等しくなります。

まとめ

この記事では、『直列接続しているコンデンサ』について、以下の内容を説明しました。