この記事では『降圧コンバータ』について
- 降圧コンバータとは
- 降圧コンバータの原理・計算式・シミュレーション
- 『降圧コンバータ』と『昇圧コンバータ』の違い
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
降圧コンバータ(降圧チョッパ)とは
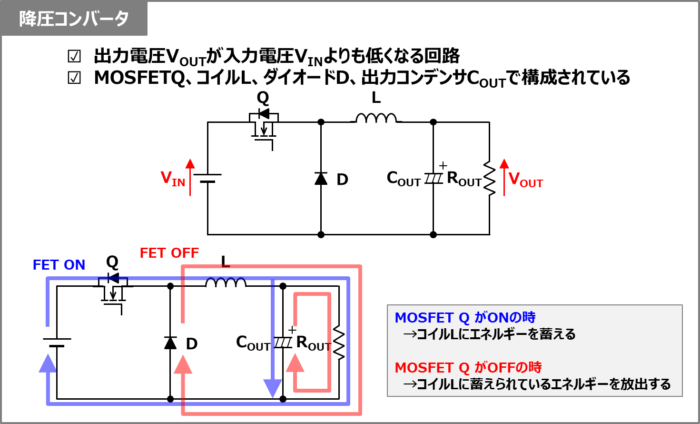
降圧コンバータは出力電圧\(V_{OUT}\)が入力電圧\(V_{IN}\)よりも低くなる回路であり、MOSFET\(Q\)、コイル(インダクタ)\(L\)、ダイオード\(D\)、出力コンデンサ\(C_{OUT}\)で構成されています。
後ほど動作原理について説明しますが、MOSFET\(Q\)のON時にコイル\(L\)にエネルギーを蓄え、MOSFET\(Q\)のOFF時にコイル\(L\)に蓄えられたエネルギーを放出しています。
MOSFET\(Q\)のON時間が長いほど、出力電圧\(V_{OUT}\)は高くなり、MOSFET\(Q\)のON時間が短いほど、出力電圧\(V_{OUT}\)は低くなります。そのため、MOSFET\(Q\)のオンデューティ比\(D\)(1周期\(T\)におけるオン期間\(T_{ON}\)の割合)を制御することで、所望の出力電圧\(V_{OUT}\)を得ることができます。
降圧コンバータのイメージ
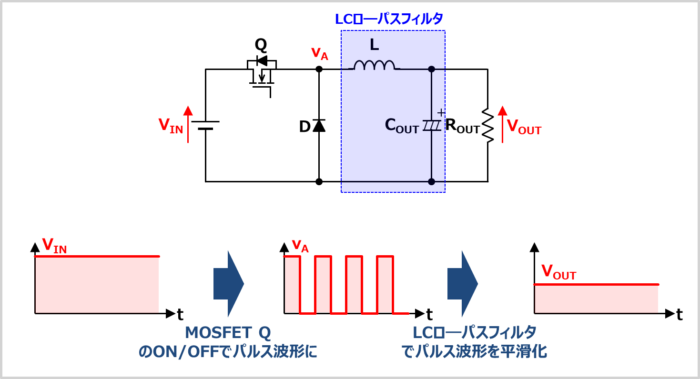
MOSFET\(Q\)をON/OFFすることで、A点の電圧\(V_A\)はパルス波形となります。このパルス電圧\(V_A\)をコイル\(L\)と出力コンデンサ\(C_{OUT}\)のLCロ―パスフィルタで平滑化していると考えると、出力電圧\(V_{OUT}\)が入力電圧\(V_{IN}\)よりも低くなるイメージが湧くと思います。
補足
- 降圧コンバータは『バックコンバータ(Buck Converter)』や『ステップ・ダウン・コンバータ』や『降圧チョッパ』とも呼ばれています。
- MOSFET\(Q\)はバイポーラトランジスタなど他のスイッチング素子でも使用可能です。
→チョッパ(Chopper)は英語で「切り刻むもの」という意味があり、MOSFET\(Q\)で電流や電圧を切り刻んで降圧しているように見えることから、降圧チョッパと呼ばれています。
降圧コンバータの動作原理
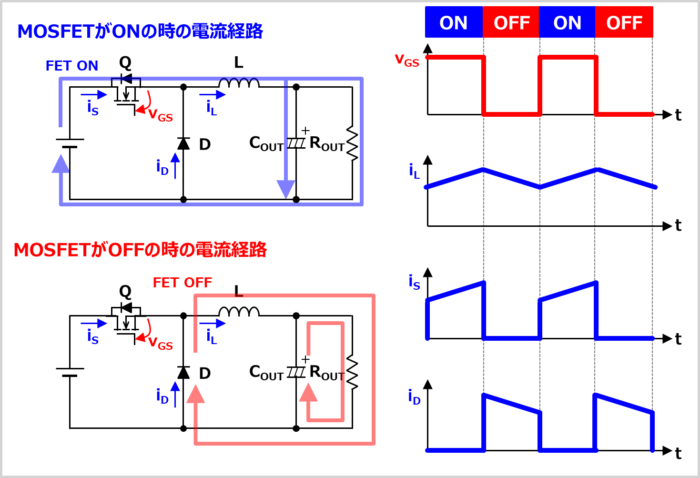
ではこれから、降圧コンバータの動作原理について説明します。MOSFET\(Q\)が『ONの時』と『OFFの時』に分けて考えます。
MOSFET\(Q\)がONの時
MOSFET\(Q\)がONの時、電流経路は『入力電圧\(V_{IN}\)→MOSFET\(Q\)→コイル\(L\)→出力部(出力コンデンサ\(C_{OUT}\)+負荷抵抗\(R_{OUT}\))』となります。この期間では、出力コンデンサ\(C_{OUT}\)を充電すると同時に、負荷抵抗\(R_{OUT}\)にも電流が流れています。
コイル\(L\)は電流の変化を妨げるように動作するため、MOSFET\(Q\)をONしても、電流は一気には流れず、コイル\(L\)に流れる電流\(i_L\)は徐々に増加します。
コイル\(L\)に電流が流れることで、エネルギーが蓄えられます。
あわせて読みたい
インダクタンス\(L{\mathrm{[H]}}\)のコイルに流れている電流が\(I{\mathrm{[A]}}\)の時、コイルに蓄えられているエネルギー\(U{\mathrm{[J]}}\)は次式で表されます。
\begin{eqnarray}
U=\frac{1}{2}LI^2{\mathrm{[J]}}
\end{eqnarray}
コイルのエネルギー\(U{\mathrm{[J]}}\)については別途下記の記事で詳しく説明していますので、ご参考にしてください。
-

コイルに蓄えられるエネルギーの『式』と『求め方』について!
続きを見る
MOSFET\(Q\)がOFFの時
MOSFET\(Q\)がOFFになると、コイル\(L\)に蓄えられているエネルギーを放出して、コイル\(L\)は電流を流し続けようとします。
そのため、この期間の電流経路は『コイル\(L\)→出力部(出力コンデンサ\(C_{OUT}\)+負荷抵抗\(R_{OUT}\))→ダイオード\(D\)』となります。また、この期間では、出力コンデンサ\(C_{OUT}\)に充電されている電荷が負荷抵抗\(R_{OUT}\)に放電されています。
コイル\(L\)は電流の変化を妨げるように動作するため、コイル\(L\)に流れる電流\(i_L\)は徐々に減少します。
降圧コンバータの出力電圧の式
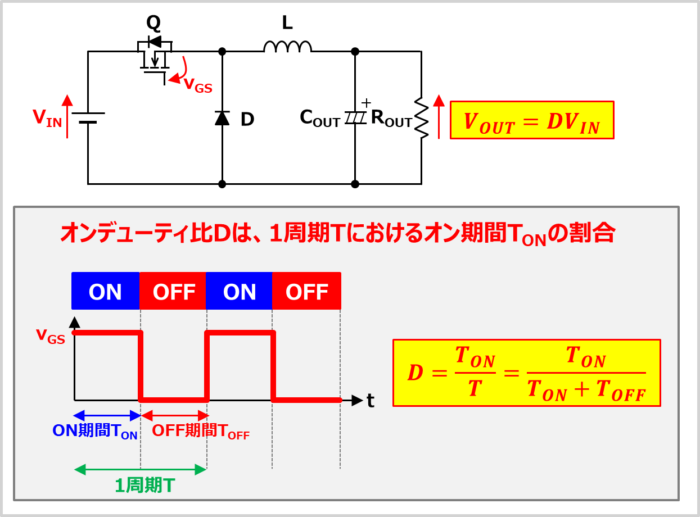

降圧コンバータの出力電圧\(V_{OUT}\)は次式となります。
V_{OUT}=DV_{IN}\tag{1}
\end{eqnarray}
上式において、オンデューティ比\(D\)はMOSFET\(Q\)の1周期\(T\)におけるオン期間\(T_{ON}\)の割合なので、次式で表されます。
\begin{eqnarray}
D=\frac{T_{ON}}{T}=\frac{T_{ON}}{T_{ON}+T_{OFF}}=T_{ON}×f_{SW}\tag{2}
\end{eqnarray}
(2)式において、\(f_{SW}\)はMOSFET\(Q\)のスイッチング周波数です。また、(2)式から分かるように、オンデューティ比\(D\)は1より小さい値なので、(1)式より出力電圧\(V_{OUT}\)は入力電圧\(V_{IN}\)よりも低くなることが分かります。
例えば、オンデューティ比\(D\)が0.5の場合(1周期\(T\)におけるオン期間\(T_{ON}\)が半分の場合)、次式に示すように理論上は出力電圧\(V_{OUT}\)は入力電圧\(V_{IN}\)の\(\displaystyle\frac{1}{2}\)倍となります(実際には、ダイオード\(D\)やMOSFET\(Q\)などの損失があるため、出力電圧\(V_{OUT}\)は\(\displaystyle\frac{1}{2}\)倍よりも小さくなります)。
\begin{eqnarray}
V_{OUT}=DV_{IN}=0.5V_{IN}=\frac{1}{2}V_{IN}\tag{3}
\end{eqnarray}
降圧コンバータのシミュレーション
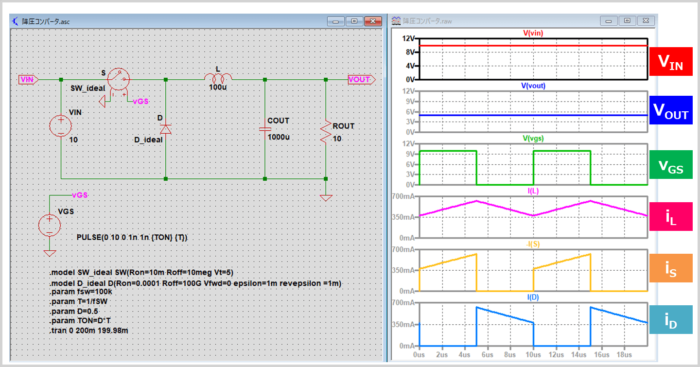

降圧コンバータをLTspiceでシミュレーションした時の結果を上図に示しています。
上図の右側に示している波形は上から
- 入力電圧\(V_{IN}\)
- 出力電圧\(V_{OUT}\)
- スイッチ\(S\)の駆動信号\(v_{GS}\)
- コイル\(L\)に流れる電流\(i_L\)
- スイッチ\(S\)に流れる電流\(i_S\)
- ダイオード\(D\)に流れる電流\(i_D\)
となっています。
シミュレーション結果を見ると、入力電圧\(V_{IN}\)は10V、オンデューティ比\(D\)は0.5なので、出力電圧\(V_{OUT}\)が5Vになっていることが確認できます。なお、シミュレーション回路ではMOSFET\(Q\)は理想スイッチ、ダイオード\(D\)は理想ダイオードを用いています。
あわせて読みたい
LTspiceで理想スイッチと理想ダイオードを作る方法については、下記の記事で説明してますので、ご参考になれば幸いです。
-


【LTspice】理想スイッチである『電圧制御スイッチ』の使い方
続きを見る
-



【LTspice】『理想ダイオード』の作成方法
続きを見る
『降圧コンバータ』と『昇圧コンバータ』の違い
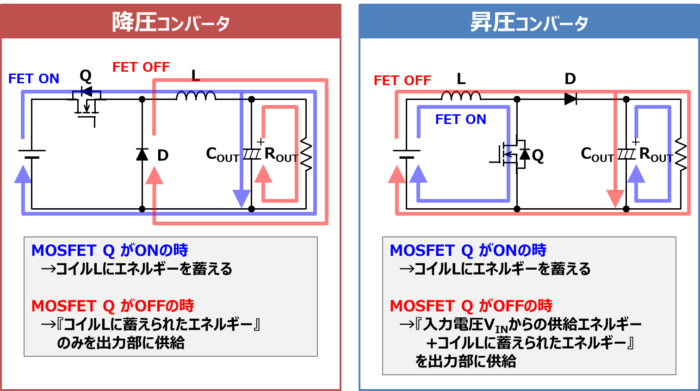

昇圧コンバータも降圧コンバータと同様に、コイル\(L\)、MOSFET\(Q\)、ダイオード\(D\)、出力コンデンサ\(C_{OUT}\)で構成されていますが、上図に示すように、各部品の接続箇所が異なります。
降圧コンバータも昇圧コンバータもMOSFET\(Q\)がオンの時にコイル\(L\)にエネルギーを蓄えるのは同じです。
降圧コンバータはMOSFET\(Q\)がOFFの時に『コイル\(L\)に蓄えられたエネルギー』のみ出力部に供給していますが、昇圧コンバータはMOSFET\(Q\)がOFFの時に『入力電圧\(V_{IN}\)からの供給エネルギー+コイル\(L\)に蓄えられたエネルギー』を出力部に供給しています。
あわせて読みたい
昇圧コンバータの原理や特徴については、下記の記事で説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-


昇圧コンバータ(昇圧チョッパ)とは?原理などを解説!
続きを見る
まとめ
この記事では『降圧コンバータ』について、以下の内容を説明しました。
- 降圧コンバータとは
- 降圧コンバータの原理・計算式・シミュレーション
- 『降圧コンバータ』と『昇圧コンバータ』の違い
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。







