【虚数単位とは】『iとjの違い』や『書き方・読み方』などを解説！

この記事では『虚数単位』について

虚数単位の『意味』と『式』
虚数単位の『記号』(数学の世界では『i』、電気の世界では『j』を用いる理由)
虚数単位の『書き方』と『読み方』
虚数単位と『ベクトルの回転』

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

虚数単位とは

虚数単位とは2乗すると『－1』になる数です。虚数単位の記号は数学の世界では『i』、電気の世界では『j』を用いています(この記事では『j』を用います)。したがって、虚数単位を式で表すと次式となります。

\begin{eqnarray}
j^2&=&-1\\
\\
j&=&\sqrt{-1}
\end{eqnarray}

例えば、\(\sqrt{-3}\)は次式に示すように変形することで、虚数単位jを用いて表現することができるようになります。

\begin{eqnarray}
\sqrt{-3}=\sqrt{-1}×\sqrt{3}=j\sqrt{3}
\end{eqnarray}

なお、虚数単位jを用いて、a+jbの形で表される数(aとbは実数)を複素数といい、aを実部、bを虚部といいます。

【虚数単位の記号】『i』と『j』の違い

虚数単位の記号は数学の世界では『i』、電気の世界では『j』を用います。

虚数単位は英語では『Imaginary Number』と書きます。数学の世界では『Imaginary Number』の頭文字をとり、虚数単位の記号に『i』を用いています。

一方、電気の世界では電流の記号に『i』を用いています。虚数単位の記号に『i』を用いると電流の記号と混同するため、記号は『j』を用いています。

なお、虚数単位の記号は、大文字ではなく小文字の『i』と『j』と書くので注意してください。

虚数単位の『書き方』と『読み方』

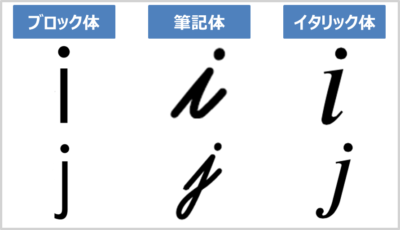
虚数単位の『書き方』

普通にアルファベットの『i』と『j』と書くだけです。ブロック体でも筆記体でもイタリック体でも構いません。ただし、イタリック体で『i』を書く場合は『z』の上に「・(ドット)」が付いているようにも見えてしまうので注意してください。

虚数単位の『読み方』

虚数単位は「きょすうたんい」と読みます。虚数単位の記号の『i』と『j』はローマ字読みで『i(あい)』と『j(じぇー)』と読みます。

虚数単位と複素平面

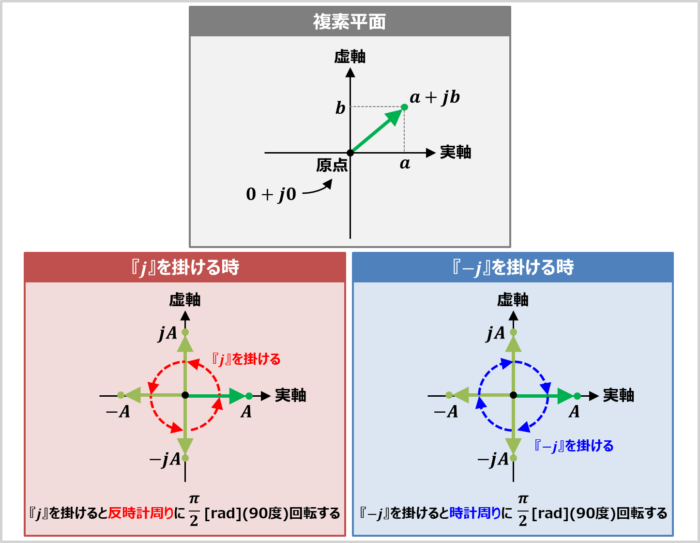
複素平面とは、その名の通り、複素数を表すための平面であり、横軸は実数の目盛(実軸)、縦軸は虚数の目盛(虚軸)となります。複素平面はガウス平面とも呼ばれています。

a+jbで表される複素数の場合、aが横軸(実軸)、bが縦軸(虚軸)に対応しています。また、実軸と虚軸の交点が原点であり、原点を複素数で表すと、0+j0となります。

虚数単位jと複素平面には下記に示す面白い性質があります。

ある実数Aに虚数単位『j』を掛けると、反時計周りに\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)回転する
ある実数Aに虚数単位『-j』を掛けると、時計周りに\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)回転する

上記の性質について、もう少し詳しく説明します。

実数Aに虚数単位『j』を掛けると、反時計周りにπ/2[rad](90度)回転する

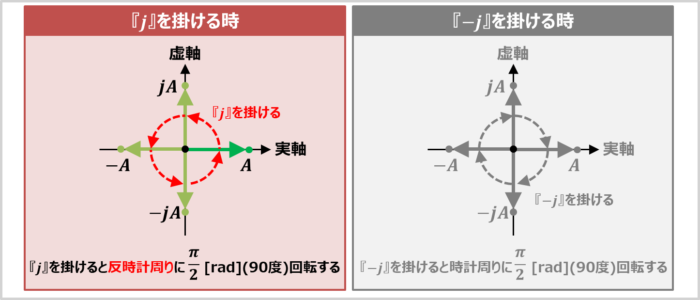
複素平面で実数Aを表すと、原点から右方向にAの距離を伸ばした位置となります。この実数Aに虚数単位『j』を掛けていくと、

\begin{eqnarray}
&&A(実数)\\
&&{\Downarrow}\\
&&A×j=jA(虚数)\\
&&{\Downarrow}\\
&&jA×j=j^2A=-A(実数)\\
&&{\Downarrow}\\
&&-A×j=-jA(虚数)\\
&&{\Downarrow}\\
&&-jA×j=-j^2A=A(実数)\\
&&{\Downarrow}\\
&&{\vdots}
\end{eqnarray}

となり、虚数単位『j』を掛ける度に、虚数になったり、実数になったりします。

複素平面上で考えると、虚数単位『j』を掛ける度に、実数Aの位置が原点を中心として、反時計周りに\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)回転しています。

実数Aに虚数単位『-j』を掛けると、反時計周りにπ/2[rad](90度)回転する

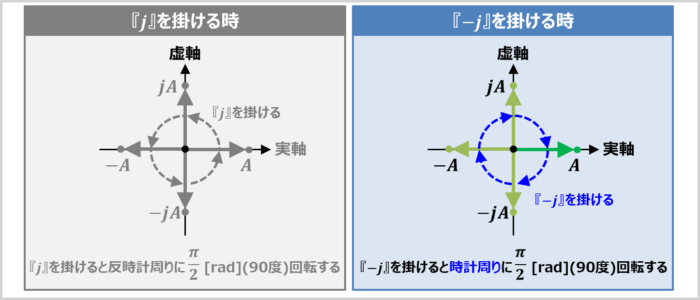
複素平面で実数Aを表すと、原点から右方向にAの距離を伸ばした位置となります。この実数Aに虚数単位『-j』を掛けていくと、

\begin{eqnarray}
&&A(実数)\\
&&{\Downarrow}\\
&&A×-j=-jA(虚数)\\
&&{\Downarrow}\\
&&-jA×-j=j^2A=-A(実数)\\
&&{\Downarrow}\\
&&-A×-j=jA(虚数)\\
&&{\Downarrow}\\
&&jA×-j=-j^2A=A(実数)\\
&&{\Downarrow}\\
&&{\vdots}
\end{eqnarray}

となり、虚数単位『-j』を掛ける度に、虚数になったり、実数になったりします。

複素平面上で考えると、虚数単位『-j』を掛ける度に、実数Aの位置が原点を中心として、時計周りに\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)回転しています。

これらの性質は交流回路をベクトルで解析する際に役に立ちます。次に簡単な例を用いて、交流回路をベクトルで解析してみましょう。

虚数単位と複素数とベクトル

『虚数単位を掛けると\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)回転する』という性質は交流回路をベクトルで解析する際に役立ちます。

まず最初に、ベクトルについて軽く説明します。

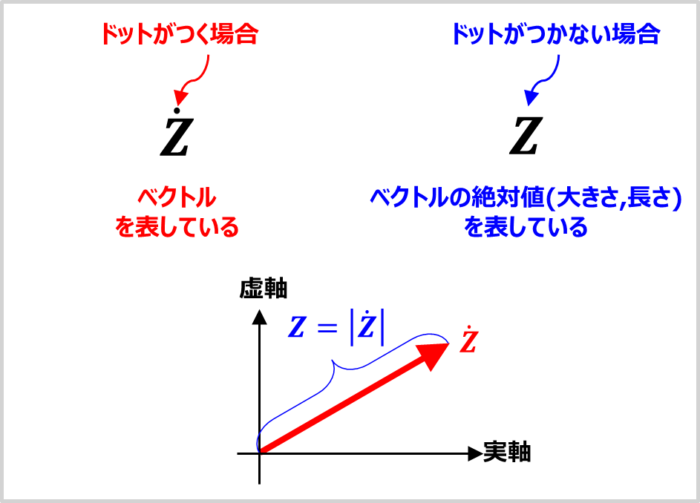
電気の世界では『インピーダンス\(Z\)』や『電圧\(V\)』や『電流\(I\)』などの記号の上に「・(ドット)」をつけることで、ベクトルを表しています。

そのため、『インピーダンス\(Z\)』や『電圧\(V\)』や『電流\(I\)』などの記号の上に「・(ドット)」がつく場合とつかない場合では下記に示すように意味が異なります。

記号の上にドットがつく場合(\({\dot{Z}}\)・\({\dot{V}}\)・\({\dot{I}}\)など)

ベクトルを表している。

記号の上にドットがつかない場合(\(Z\)・\(V\)・\(I\)など)

ベクトルの絶対値(大きさ,長さ)を表している。

『インピーダンス\(Z\)』や『電圧\(V\)』や『電流\(I\)』をベクトル表記(\({\dot{Z}}\)・\({\dot{V}}\)・\({\dot{I}}\))にすることで、「大きさ」と「位相」の両方を表すことができます。なお、ベクトルの向きの角度が「位相」を表します。

ベクトル表記について詳しい内容を知りたい方は下記の記事で説明していますので、ご参考になれば幸いです。

【交流回路とベクトル】インピーダンスなどにつく「・(ドット)」の意味！

コイルに流れる電流\({\dot{I}_L}\)とコイルにかかる電圧\({\dot{V}_L}\)を『複素数』と『ベクトル図』で表す

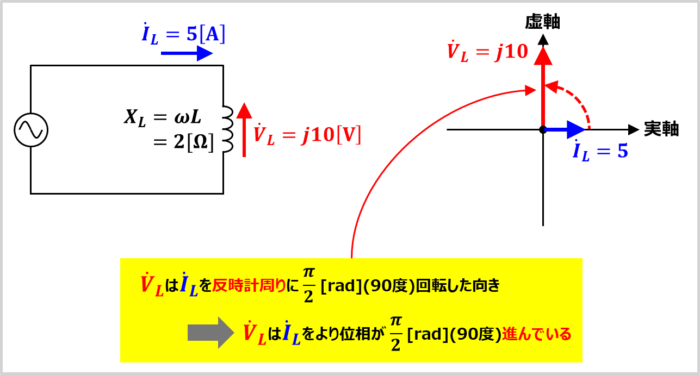
ここで、一例として、コイルに流れる電流の大きさ\(I_L\)が5[A]、コイルのリアクタンス\(X_L(={\omega}L)\)が2[Ω]の時において、コイルに流れる電流\({\dot{I}_L}\)とコイルにかかる電圧\({\dot{V}_L}\)を『複素数』と『ベクトル図』で表してみましょう。

まず、交流回路をベクトルで解析する際には、基準となるベクトルを最初に決めます。ここでは、コイルに流れる電流\({\dot{I}_L}\)を基準として考えます。基準ベクトルの向きを実軸の向き(右向き)とすると、コイルに流れる電流\({\dot{I}_L}\)は次式の複素数で表すことができます。

\begin{eqnarray}
{\dot{I}_L}=5+j0=5{\mathrm{[A]}}
\end{eqnarray}

また、コイルのインピーダンス\({\dot{Z}_L}\)は次式で表されます。

\begin{eqnarray}
{\dot{Z}_L}=j{\omega}L=jX_L=j2{\mathrm{[{\Omega}]}}
\end{eqnarray}

したがって、コイルにかかる電圧\({\dot{V}_L}\)は次式で表すことができます。

\begin{eqnarray}
{\dot{V}_L}={\dot{I}_L}×{\dot{Z}_L}=5×j2=j10{\mathrm{[V]}}
\end{eqnarray}

上式より、コイルにかかる電圧\({\dot{V}_L}\)は虚軸の向き(上向き)になります。言い換えれば、コイルにかかる電圧\({\dot{V}_L}\)はコイルに流れる電流\({\dot{I}_L}\)を反時計周りに\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)回転した向きとなります。

また、交流回路をベクトルで表す時には下記のルールがあります。

交流回路のベクトルで表す時のルール

ベクトルが基準から反時計周りに\({\theta}{\mathrm{[rad]}}\)回転している場合、位相が\({\theta}{\mathrm{[rad]}}\)進んでいる。
ベクトルが基準から時計周りに\({\theta}{\mathrm{[rad]}}\)回転している場合、位相が\({\theta}{\mathrm{[rad]}}\)遅れている。

以上より、コイルにかかる電圧\({\dot{V}_L}\)はコイルに流れる電流\({\dot{I}_L}\)より位相が\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)進んでいるということになります。

コンデンサに流れる電流\({\dot{I}_C}\)とコンデンサにかかる電圧\({\dot{V}_C}\)を『複素数』と『ベクトル図』で表す

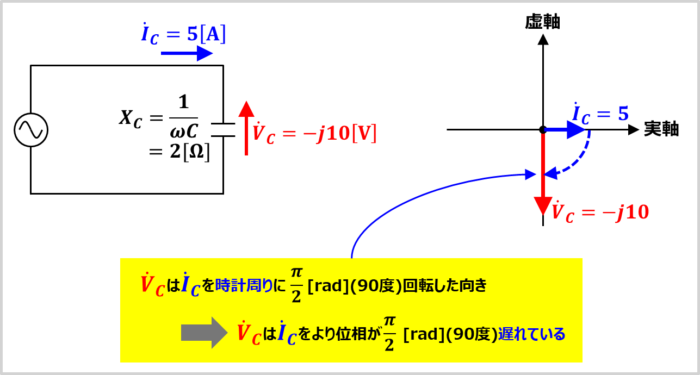
ここで、一例として、コンデンサに流れる電流の大きさ\(I_C\)が5[A]、コンデンサのリアクタンス\(X_C(=\displaystyle\frac{1}{{\omega}C})\)が2[Ω]の時において、コンデンサに流れる電流\({\dot{I}_C}\)とコンデンサにかかる電圧\({\dot{V}_C}\)を『複素数』と『ベクトル図』で表してみましょう。

ここでは、コンデンサに流れる電流\({\dot{I}_C}\)を基準として考えます。基準ベクトルの向きを実軸の向き(右向き)とすると、コンデンサに流れる電流\({\dot{I}_C}\)は次式の複素数で表すことができます。

\begin{eqnarray}
{\dot{I}_C}=5+j0=5{\mathrm{[A]}}
\end{eqnarray}

また、コンデンサのインピーダンス\({\dot{Z}_C}\)は次式で表されます。

\begin{eqnarray}
{\dot{Z}_C}=\displaystyle\frac{1}{j{\omega}C}=-j\displaystyle\frac{1}{{\omega}C}=-jX_C=-j2{\mathrm{[{\Omega}]}}
\end{eqnarray}

したがって、コンデンサにかかる電圧\({\dot{V}_C}\)は次式で表すことができます。

\begin{eqnarray}
{\dot{V}_C}={\dot{I}_C}×{\dot{Z}_C}=5×-j2=-j10{\mathrm{[V]}}
\end{eqnarray}

上式より、コンデンサにかかる電圧\({\dot{V}_C}\)は虚軸の向き(下向き)になります。言い換えれば、コンデンサにかかる電圧\({\dot{V}_C}\)はコンデンサに流れる電流\({\dot{I}_C}\)を時計周りに\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)回転した向きとなります。

以上より、コンデンサにかかる電圧\({\dot{V}_C}\)はコンデンサに流れる電流\({\dot{I}_C}\)より位相が\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(90度)遅れているということになります。