ツェナーダイオードの『許容損失』について！

この記事ではツェナーダイオードの『許容損失』について

ツェナーダイオードの『許容損失』とは
許容損失の『P_d-T_a特性(電力軽減曲線)』

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

ツェナーダイオードの『許容損失』

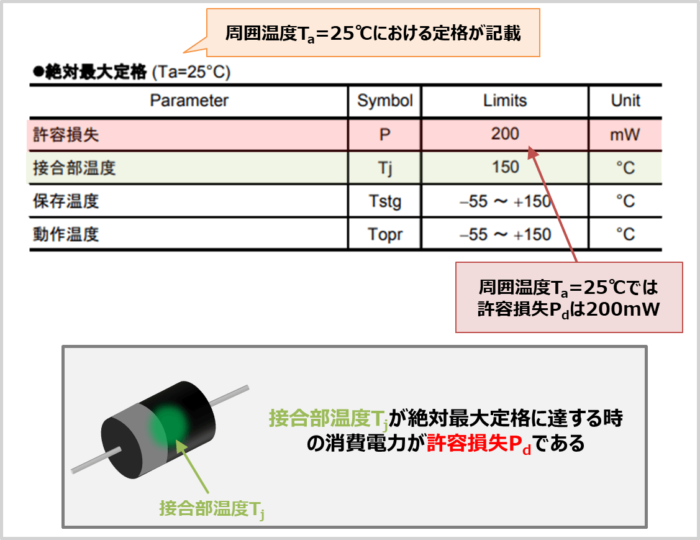
ツェナーダイオードの許容損失P_dは、『接合部温度T_jが絶対最大定格に達する時の消費電力』です。許容損失の記号はデータシートにより異なりますが、『P_d』や『P_T』や『P_tot』や『P』で表されることが多いです。

データシート上に記載されている許容損失P_dは『周囲温度T_a=25℃』を基準にしています。そのため、接合部温度T_jが『25℃』から『接合部温度T_jの絶対最大定格T_j(MAX)』に達するときの消費電力がデータシート上に記載されている許容損失P_dとなります。許容損失P_dは熱抵抗R_th(j-c)を用いると、次式で表されます。

許容損失の理論式

\begin{eqnarray}
P_{d}=\frac{T_{j(MAX)}-T_a}{R_{th(j-c)}}=\frac{T_{j(MAX)}-25}{R_{th(j-c)}}\tag{1}
\end{eqnarray}

上図に示しているデータシートはローム製ツェナーダイオードUDZVシリーズの絶対最大定格です。データシートを見ると、許容損失P_dが200mWであることが確認できます(データシート上では許容損失の記号が'P'になっています)。

また、データシートより許容損失P_d、接合部温度T_j、周囲温度T_aが分かるので、(1)式より、熱抵抗R_th(j-c)を求めることもできます。熱抵抗R_th(j-c)は以下の値となります。

\begin{eqnarray}
R_{th(j-c)}=\frac{T_{j(MAX)}-T_a}{P_{d}}=\frac{150{\mathrm{[{^{\circ}C}]}}-25{\mathrm{[{^{\circ}C}]}}}{200{\mathrm{[mW]}}}=0.625{\mathrm{[{^{\circ}C}/mW]}}\tag{2}
\end{eqnarray}

補足

許容損失は英語では『Power Dissipation』や『Total Power Dissipation』と書きます。
チップ部品の場合、実装基板により許容損失が異なりますので注意してください。

許容損失の『P_d-T_a特性(電力軽減曲線)』

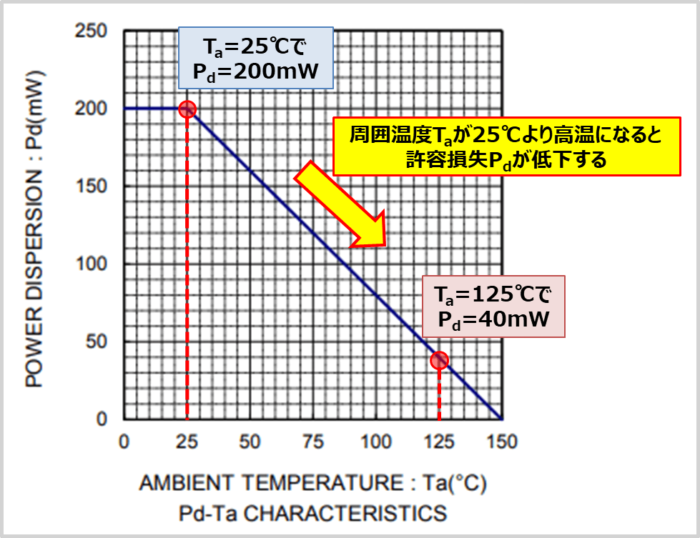
データシート上に記載されている許容損失P_dは『周囲温度T_a=25℃』を基準にしているため、T_a=25℃よりも温度が高い場合は、許容損失P_dが低下します。データシートにはそれを示す『P_d-T_a特性(電力軽減曲線)』が記載されています。

上図に示しているのはローム製ツェナーダイオードUDZVシリーズの『P_d-T_a特性(電力軽減曲線)』です。周囲温度T_aが25℃の時の許容損失P_dは200mWですが、周囲温度T_aが25℃よりも高くなると、許容損失P_dが低下していることが確認できます。

例えば、周囲温度T_aが125℃の場合には、許容損失P_dが40mWになってしまいます。そのため、周囲温度T_aに応じて許容損失P_dを軽減する必要があります。

なお、(1)式でも各周囲温度により許容損失P_dを求めることが可能です。周囲温度T_a=125℃を(1)式に代入すると、

\begin{eqnarray}
P_{d}=\frac{T_{j(MAX)}-T_a}{R_{th(j-c)}}=\frac{150{\mathrm{[{^{\circ}C}]}}-125{\mathrm{[{^{\circ}C}]}}}{0.625{\mathrm{[{^{\circ}C}/mW]}}}=40{\mathrm{[mW]}}\tag{3}
\end{eqnarray}

となり、『P_d-T_a特性(電力軽減曲線)』での値と一致することが分かります。