電圧や電力の『デシベル(dB)』とは？計算方法や変換方法について

増幅回路やフィルタ回路などで電圧、電流、電力のゲインの計算を行う際に、デシベル(dB)という単位が使われることが多いです。
この記事では、このデシベル(dB)について計算方法や変換方法などを詳しく説明します。

ゲイン(利得、増幅度・増幅率)とは

デシベル(dB)との関連用語であるゲインについてまず説明します。

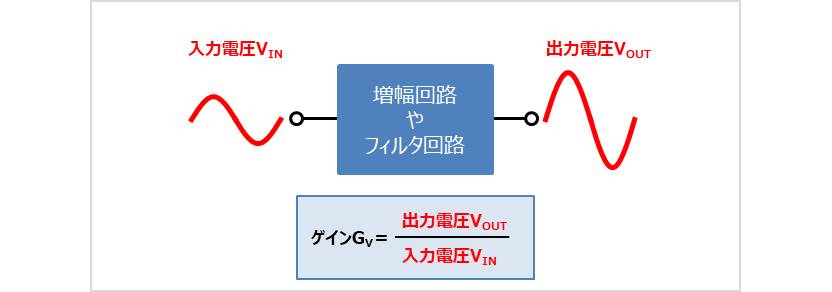
ゲインとは増幅回路やフィルタ回路における入力と出力の比です。「出力/入力」は電圧、電流、電力のどれかになります。この記事では、電圧の場合を一例にとってゲインを説明します。

増幅回路やフィルタ回路の入力に入力電圧\(V_{IN}\)を入力すると、出力電圧\(V_{OUT}\)には入力電圧\(V_{IN}\)が増幅または減衰されたものが現れます。この入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の比をゲイン\(G_{V}\)と呼び、ゲイン\(G_{V}\)は出力電圧\(V_{OUT}\)の大きさを入力電圧\(V_{IN}\)の大きさで割ったもので表されます。

式で表すと以下のようになります。
\begin{eqnarray}
G_{V}=\frac{V_{OUT}}{V_{IN}}
\end{eqnarray}
上記の式の単位は[倍]であり、デシベル(dB)ではありません。次にデシベルについて説明します。

デシベルとは？計算方法について

ゲインの常用対数\({\log_{10}}\)を10倍もしくは20倍したものの単位がデシベル(dB)となります。

電力のゲイン\(G_{P}\)をデシベルで表す場合、ゲインの常用対数(\({\log_{10}}\))を10倍します。式で表すと以下のようになります。

電圧のゲイン\(G_{V}\)、電流のゲイン\(G_{I}\)をデシベルで表す場合、ゲインの常用対数(\({\log_{10}}\))を20倍します。式で表すと以下のようになります。

例えば、入力電圧\(V_{IN}\)に対して出力電圧が\(V_{OUT}\)が1000000倍(10⁷倍)の時、デシベル表記では以下のようになります。
\begin{eqnarray}
G_{V}=20{\log_{10}}\frac{V_{OUT}}{V_{IN}}=20{\log_{10}}10^7=140{\mathrm{[dB]}}
\end{eqnarray}
単位がデシベル(dB)の場合、10000000倍という大きな数字を140[dB]という小さな数字で表現することができます。このように、常用対数をとることにより大きな数を少なくでき、計算がしやすくなります。

デシベルから電圧、電流、電力への変換方法について

デシベル(dB)の値が分かっている時において、電圧、電流、電力へ変換する方法を説明します。

電圧のゲイン\(G_{V}\)(dB)から入力電圧\(V_{IN}\)や出力電圧\(V_{OUT}\)を求める場合、
\begin{eqnarray}
G_{V}&=&20{\log_{10}}\frac{V_{OUT}}{V_{IN}}\\
{\Leftrightarrow}\frac{V_{OUT}}{V_{IN}}&=&10^{\cfrac{G_{V}}{20}}
\end{eqnarray}
となります。
電流のゲイン\(G_{I}\)(dB)から入力電圧\(I_{IN}\)や出力電圧\(I_{OUT}\)を求める場合、
\begin{eqnarray}
G_{I}&=&20{\log_{10}}\frac{I_{OUT}}{I_{IN}}\\
{\Leftrightarrow}\frac{I_{OUT}}{I_{IN}}&=&10^{\cfrac{G_{I}}{20}}
\end{eqnarray}
となります。
電力のゲイン\(G_{P}[dB]\)から入力電力\(P_{IN}\)や出力電力\(P_{OUT}\)を求める場合、
\begin{eqnarray}
G_{P}&=&10{\log_{10}}\frac{P_{OUT}}{P_{IN}}\\
{\Leftrightarrow}\frac{P_{OUT}}{P_{IN}}&=&10^{\cfrac{G_{P}}{10}}
\end{eqnarray}
となります。

デシベルと数値の変換表

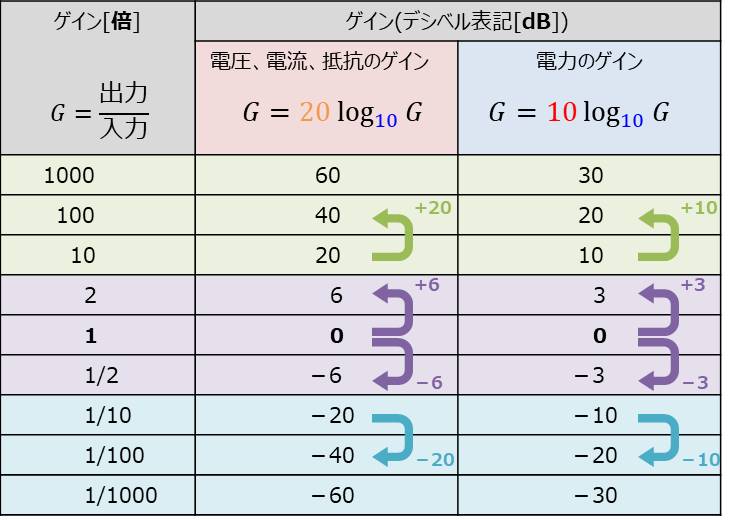
上表にデシベルと数値の変換表を示しています。電圧、電流、抵抗はゲインが2倍になるごとに6dB変化します。また、10倍になるごとに20dB変化します。

一方、電力はゲインが2倍になるごとに3dB変化します。また、10倍になるごとに10dB変化します。
 

『電力のゲインの係数』が10で『電圧のゲインの係数』が20の理由

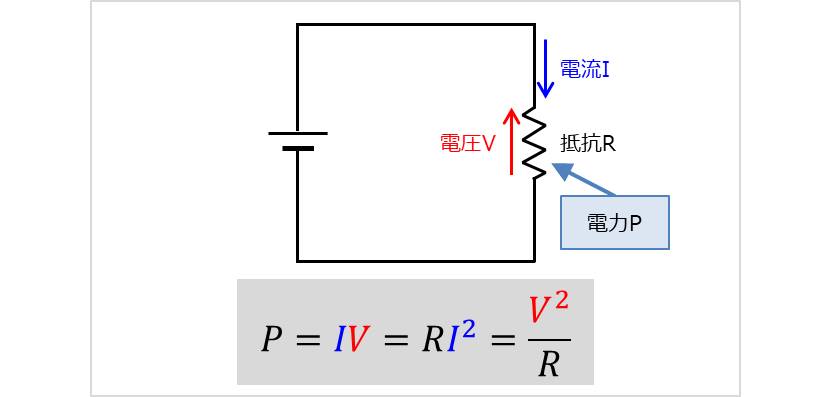
例えば、上図において、抵抗\(R\)で消費される電力\(P{\mathrm{[W]}}\)と電流\(I{\mathrm{[A]}}\)、電圧\(V{\mathrm{[V]}}\)、抵抗\(R{\mathrm{[{\Omega}]}}\)の関係は以下の式となります。
\begin{eqnarray}
P=I×V=R×I^2=\frac{V^2}{R}
\end{eqnarray}

上式より、

例えば、以下の式のように『電力のゲインの係数』も『電圧のゲインの係数』も10の場合を考えてみます。
\begin{eqnarray}
G_{P}&=&10{\log_{10}}G_{P}=10{\log_{10}}\frac{P_{OUT}}{P_{IN}}\\
G_{V}&=&10{\log_{10}}G_{V}=10{\log_{10}}\frac{V_{OUT}}{V_{IN}}
\end{eqnarray}
上の関係をデシベルで表現しようとすると、

このように、電圧\(V\)の3dBの増加が電力\(P\)の6dBの増加となり、ややこしくなります。

そこで、同じデシベル値となるように、『電圧のゲインの係数』を10ではなく20とします。電力\(P\)が電圧\(V\)の2乗に比例することから、対数計算では『電力のゲインの係数』の10に対して、2倍の補正を行うのです。これが、『電力のゲインの係数』が10で『電圧のゲインの係数』が20の理由です。
\begin{eqnarray}
G_{P}&=&10{\log_{10}}G_{P}=10{\log_{10}}\frac{P_{OUT}}{P_{IN}}\\
G_{V}&=&20{\log_{10}}G_{V}=20{\log_{10}}\frac{V_{OUT}}{V_{IN}}
\end{eqnarray}
このように『電圧のゲインの係数』が20の場合、上の関係をデシベルで表現しようとすると、

電圧と電力のデシベル値が同じになっていることが確認できます。

数値の掛け算はデシベルでは足し算となる

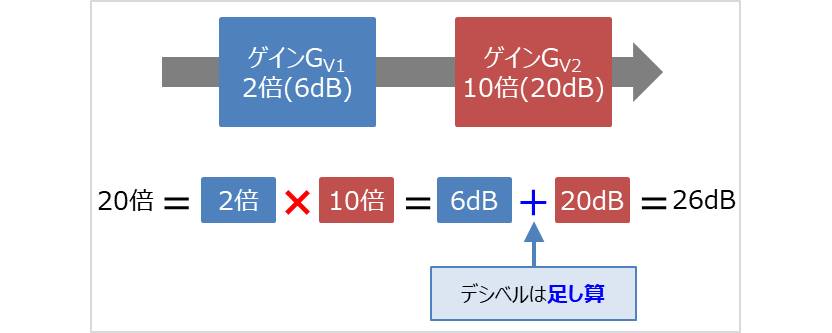
ゲイン\(G_{V1}\)が2倍である増幅回路とゲイン\(G_{V2}\)が10倍である増幅回路が直列に接続されている構成を考えてみます。ゲイン\(G_{V1}\)が2倍である増幅回路のゲイン\(G_{V1}\)をデシベル表記すると、
\begin{eqnarray}
G_{V1}=20{\log_{10}}G_{V1}=20{\log_{10}}2=6{\mathrm{[dB]}}
\end{eqnarray}
となります。
ゲイン\(G_{V2}\)が10倍である増幅回路のゲイン\(G_{V2}\)をデシベル表記すると
\begin{eqnarray}
G_{V2}=20{\log_{10}}G_{V2}=20{\log_{10}}10=20{\mathrm{[dB]}}
\end{eqnarray}
となります。
そこで、各増幅回路は直列接続されているため、出力に現れる電圧は入力の2×10=20倍となります。そこで20倍をデシベル表記で表すと、
\begin{eqnarray}
G=20{\log_{10}}G=20{\log_{10}}20=26{\mathrm{[dB]}}=6{\mathrm{[dB]}}+20{\mathrm{[dB]}}
\end{eqnarray}
となります。26[dB]はゲイン\(G_{V1}\)とゲイン\(G_{V2}\)の足し算であることが分かります。
 

【その他】デシベルの単位(dBV,dBm)について

デシベル[dB]には[dBV][dBmV][dBμV][dBm]などの関連単位があります。各単位について説明します。

• dBV

1Vを基準とした単位は[dBV]で表示します。例えば、0dBVの場合には1Vということになります。

• dBmV

1mVを基準とした単位は[dBmV]で表示します。

• dBμV

1μV=10^-6Vを基準した単位は[dBμV]で表示します。

• dBW

1Wを基準した単位は[dBW]で表示します。

• dBm

1mWを基準した単位は[dBm]で表示します。

まとめ

この記事では、『デシベル(dB)』について、以下の内容を説明しました。

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。

全記事一覧