振動試験とは？『目的』や『種類(正弦波、ランダム)』を解説！

この記事では『振動試験』について

振動試験とは
振動試験の種類(正弦波振動試験とランダム振動試験)
振動試験の加速度って何？

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

振動試験とは

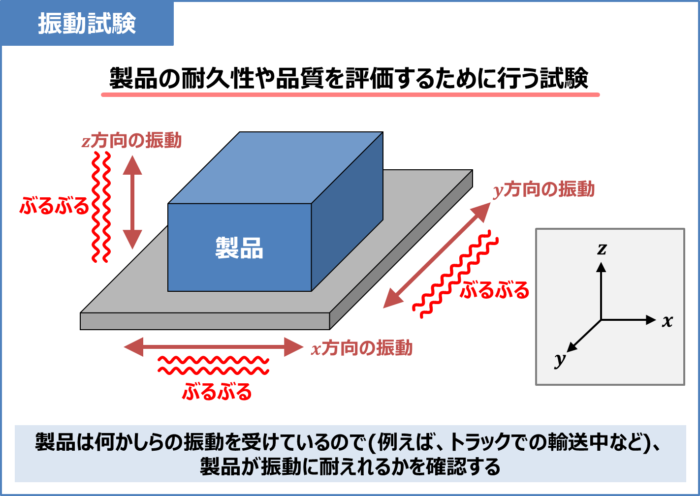
振動試験は製品(電気機器や電源ユニットなど)の耐久性や品質を評価するために行います。

製品は何かしらの振動を受けているので(例えば、トラックでの輸送中に生じる振動など)、製品が振動に耐えられるかを確認するために、振動試験を行います。

電源ユニットの場合、無通電状態で振動試験を実施後、半田クラック等が生じていないかを確認します。その後、通電して出力電圧や効率等の電気的特性に変化がないかを確認します。半田クラック等の問題が発生した場合には、「はんだ盛り」や「ランド径の変更」などの対策を行います。

振動試験の種類

振動試験は主に「正弦波振動試験」と「ランダム振動試験」に分類することができます。また、正弦波振動試験には「正弦波一定振動試験」と「正弦波掃引振動試験」の2種類があります。

正弦波振動試験(正弦波一定振動試験)

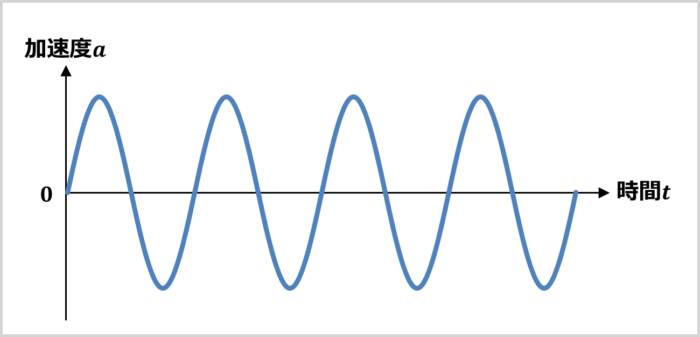
正弦波一定振動試験は、任意の1つの周波数の振動を一定時間かけ続ける振動試験です。固定振動数試験や単一正弦波試験やポイント試験とも呼ばれています。

なお、試験条件には下記のようなものがあります。

正弦波一定振動試験の試験条件

振動の周波数\({\mathrm{[Hz]}}\)
加速度\({\mathrm{[m/s^2{\;}or{\;}G]}}\)
変位\({\mathrm{[mm_{0-p}{\;}or{\;}mm_{p-p}]}}\)
- →変位は片振幅\({\mathrm{[mm_{0-p}]}}\)か全振幅\({\mathrm{[ mm_{p-p}]}}\)かを選択します。
振動方向
- →x方向、y方向、z方向の振動かを選択します。
試験時間\({\mathrm{[s]}}\)

正弦波振動試験(正弦波掃引振動試験)

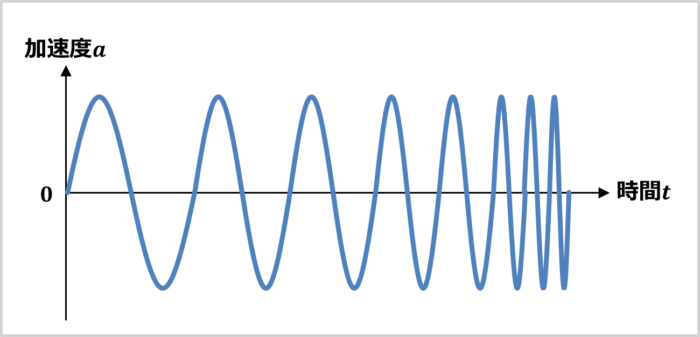
正弦波掃引振動試験は、周波数を徐々に変化させながら、振動を一定時間かけ続ける振動試験です。周波数掃引振動試験やスイープ試験とも呼ばれています。

なお、試験条件には下記のようなものがあります。

正弦波掃引振動試験の試験条件

振動の周波数範囲\({\mathrm{[Hz]}}\)
加速度\({\mathrm{[m/s^2{\;}or{\;}G]}}\)
変位\({\mathrm{[mm_{0-p}{\;}or{\;}mm_{p-p}]}}\)
- →変位は片振幅\({\mathrm{[mm_{0-p}]}}\)か全振幅\({\mathrm{[ mm_{p-p}]}}\)かを選択します。
掃引速度\({\mathrm{[oct/min{\;}or{\;}Hz/s]}}\)
掃引時間\({\mathrm{[s]}}\)
振動方向
- →x方向、y方向、z方向の振動かを選択します。
試験時間\({\mathrm{[s]}}\)

補足

正弦波振動試験は「IEC 60068-2-6/JIS C 60068-2-6」の規格等で規定されています。
\(1{\mathrm{[G]}}=9.8{\mathrm{[m/s^2]}}\)なので、加速度の単位を\({\mathrm{[m/s^2]}}\)から\({\mathrm{[ G]}}\)に変える場合には、\(9.8\)で割ってください。

ランダム振動試験

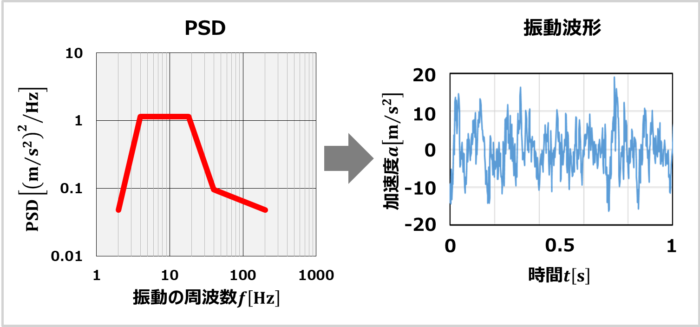
ランダム振動試験は、その名の通り、ランダムな振動を一定時間かけ続ける振動試験です。

ランダム振動試験は、複数の正弦波を合成したものです。フーリエ変換を用いると、振動の周波数と振幅が異なる正弦波の合成波として表すことができます。ランダム振動試験は、多くの振動成分で振動させることで、実際の振動に近い振動環境を再現しています。また、多くの振動成分で振動させているので、短時間で共振現象を捉えることもできます。

振動の周波数ごとの強さは、パワースペクトル密度(PSD: Power Spectral Density)\({\mathrm{[(m/s^2)^2/Hz]}}\)で設定します。PSDで周波数ごとの強さに強弱をつけることで、実際の振動に近い振動環境を再現できるのです。

補足

ランダム振動試験は「IEC 60068-2-64/JIS C 60068-2-64」の規格等で規定されています。

振動試験の加速度とは

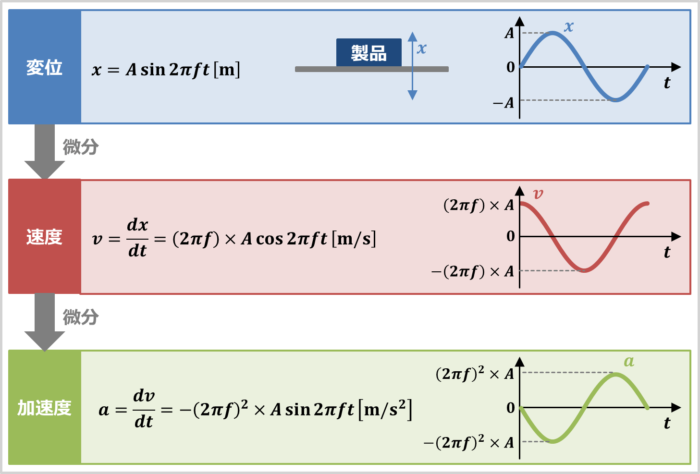
加速度とは、単位時間当たりの速度\(v\)の変化量です。例えば、\(1{\mathrm{[m/s^2]}}\)の場合、1秒間に\(1{\mathrm{[m/s]}}\)変化するということです。加速度\(a\)は速度\(v\)を時間\(t\)で微分すると求めることができます。

上図に示しているのは、変位\(x{\mathrm{[m]}}\)と速度\(v{\mathrm{[m/s]}}\)と加速度\(a{\mathrm{[m/s^2]}}\)の関係です。なお、変位とは、測定対象の移動量のことを表しています。

振動試験によって、ある製品が上下に振動している状態を考えてみましょう。製品の変位\(x{\mathrm{[m]}}\)は時間\(t\)と共に変化します。この変位\(x{\mathrm{[m]}}\)をグラフで描くと、横軸が時間\(t{\mathrm{[s]}}\)で縦軸が変位\(x{\mathrm{[m]}}\)になります。ここで、変位\(x{\mathrm{[m]}}\)を次式で表すとします。

\begin{eqnarray}
x=A{\sin}2{\pi}f{\mathrm{[m]}}\tag{1}
\end{eqnarray}

この変位\(x{\mathrm{[m]}}\)を微分したものが速度\(v{\mathrm{[m/s]}}\)になるため、速度\(v{\mathrm{[m/s]}}\)は次式となります。

\begin{eqnarray}
v=\frac{dx}{dt}=(2{\pi}f)×A{\cos}2{\pi}f{\mathrm{[m/s]}}\tag{2}
\end{eqnarray}

この速度\(v{\mathrm{[m/s]}}\)を微分すると、加速度\(a{\mathrm{[m/s^2]}}\)となり、次式となります。

\begin{eqnarray}
a=\frac{dv}{dt}=-(2{\pi}f)^2×A{\sin}2{\pi}f{\mathrm{[m/s^2]}}\tag{3}
\end{eqnarray}

つまり、加速度\(a\)は振動の周波数\(f\)と製品の移動量\(A\)で決まります。

振動試験において、製品の移動量\(A\)は、(3)式より次式で表されます。

\begin{eqnarray}
A=\frac{a}{(2{\pi}f)^2}{\mathrm{[m]}}\tag{4}
\end{eqnarray}

例えば、加速度\(a\)が\(19.6{\mathrm{[m/s^2]}}\)で振動の周波数\(f\)が\(10{\mathrm{[Hz]}}\)の時、物体の移動量\(A\)は以下の値になります。

\begin{eqnarray}
A&=&\frac{a}{(2{\pi}f)^2}\\
\\
&=&\frac{19.6}{(2{\pi}×10)^2}\\
\\
&=&4.96×10^{-3}{\mathrm{[m]}}\\
\\
&=&4.96{\mathrm{[mm]}}\tag{5}
\end{eqnarray}