【RL直列回路のラプラス変換】『過渡現象』の解き方！

この記事ではRL直列回路の『ラプラス変換による過渡現象の解き方』について説明しています。

分かりやすく説明するために、図を多く用いており、式の導出過程も細かく書くように意識しています。

【RL直列回路】『過渡現象』の式とグラフ

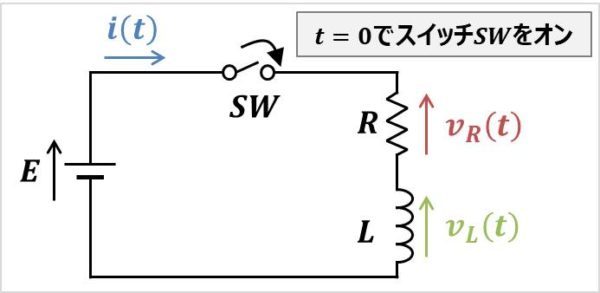
上図は抵抗\(R{\mathrm{[Ω]}}\)、インダクタ\(L{\mathrm{[H]}}\)、直流電源\(E{\mathrm{[V]}}\)、スイッチ\(SW\)からなるRL直列回路です。

この記事では、以下の条件における『過渡現象』の式を導出します。

条件

スイッチ\(SW\)をオンした時の時間\(t\)を\(t=0{\mathrm{[s]}}\)とする。

スイッチ\(SW\)をオンすると、以下の過渡現象が生じます。

電流\(i(t)\)が\(0{\mathrm{[A]}}\)から増加する。
ある程度時間が経過すると、電流\(i(t)\)の変化がなくなり、一定値\(\displaystyle\frac{E}{R}{\mathrm{[A]}}\)となる。また、その時、インダクタ\(L\)が短絡されたような状態であり、抵抗\(R\)の電圧\(v_{R}(t)\)が電源電圧の電圧\(E\)と等しくなる。

この時、電流\(i(t)\)が一定値\(\displaystyle\frac{E}{R}{\mathrm{[A]}}\)となった状態を「定常状態」、「定常状態」に至るまでの状態を「過渡状態」、その過程で見られる現状を「過渡現象」といいます。

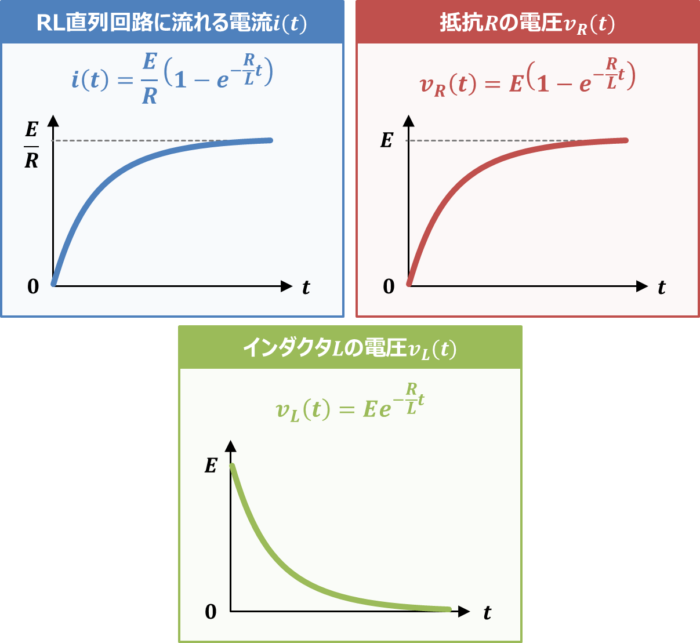
また、RL直列回路に流れる電流\(i(t)\)、抵抗\(R\)の電圧\(v_{R}(t)\)、インダクタ\(L\)の電圧\(v_{L}(t)\)の式とグラフは下記となります。

\begin{eqnarray}
i(t)&=&\frac{E}{R}\left(1-e^{-\frac{R}{L}t}\right)\\
v_{R}(t)&=&E\left(1-e^{-\frac{R}{L}t}\right)\\
v_{L}(t)&=&Ee^{-\frac{R}{L}t}
\end{eqnarray}

この記事では上式をラプラス変換を用いて解いていきます。なお、上式は微分方程式を解く最も基本的なパターンの変数分離形の微分方程式にして、直接解くことも可能です。

変数分離形の微分方程式にして、直接解く方法については以下の記事に詳しく説明していますので、参考にしてください。

: 【RL直列回路の微分方程式】『過渡現象』の解き方！
続きを見る

【RL直列回路】『ラプラス変換』による解き方

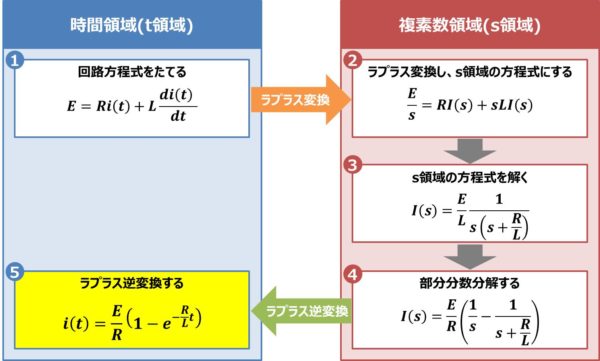
ラプラス変換を用いてRL直列回路の過渡現象を解く場合、以下の①～⑤の手順で行います。

ラプラス変換の手順

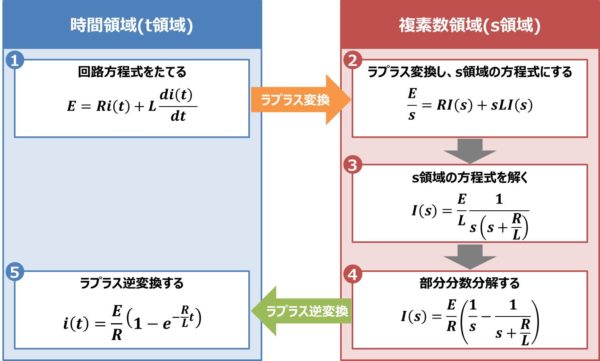
回路方程式をたてる

→対象となる回路(今回はRL直列回路)のt関数による回路方程式をたてます。

ラプラス変換し、s領域の方程式にする

→①で求めた回路方程式をラプラス変換して、s領域の方程式にします。この際、初期条件も考慮する必要があります。

s領域の方程式を解く

→求めたいs関数の式にします。今回は『\(I(s)={\cdots}\)』の式にします。

部分分数分解する

→ラプラス逆変換をするために、③で求めた式を部分分数分解します。

ラプラス逆変換する

→④で求めた式をラプラス逆変換して、t領域の方程式にします。

ではこれから、各手順について順番に説明していきます。

【RL直列回路】回路方程式をたてる

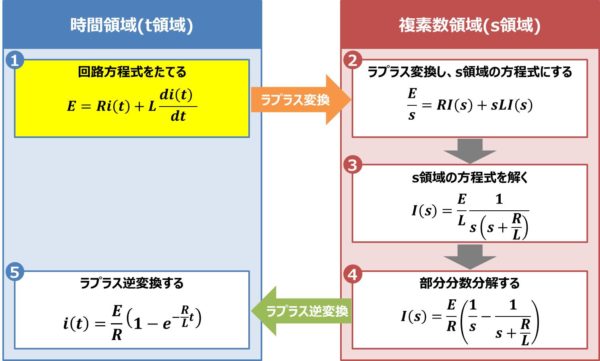
RL直列回路を下図に示します。

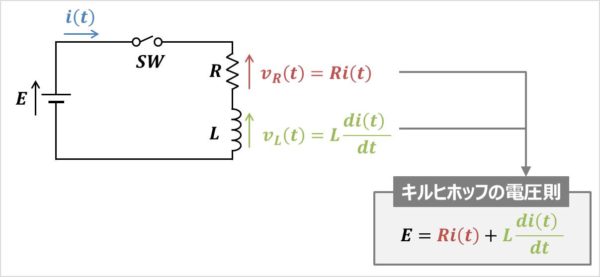
上図のRL直列回路にキルヒホッフの電圧則(キルヒホッフの第二法則)を用いると次式が成り立ちます。

\begin{eqnarray}
E=v_{R}(t)+v_{L}(t)\tag{1}
\end{eqnarray}

(1)式において、抵抗\(R\)の電圧\(v_{R}(t)\)とインダクタ\(L\)の電圧\(v_{L}(t)\)は次式で表されます。

\begin{eqnarray}
v_{R}(t)&=&Ri(t)\tag{2}\\
v_{L}(t)&=&L\frac{di(t)}{dt}\tag{3}
\end{eqnarray}

(2)式と(3)式を(1)式に代入すると、次式が得られます。

\begin{eqnarray}
E&=&v_{R}(t)+v_{L}(t)\\
&=&Ri(t)+L\frac{di(t)}{dt}\tag{4}
\end{eqnarray}

上式が、RL直列回路のt領域の回路方程式となります。

【RL直列回路】ラプラス変換し、s領域の方程式にする

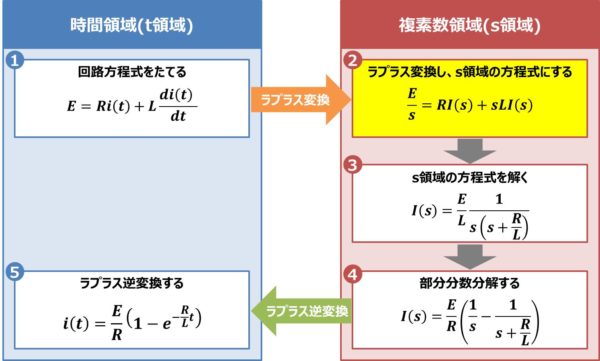
(4)式の左辺は『\(E=E{\;}{\cdot}{\;}1\)』であるため、(4)式をラプラス変換すると、次式となります。

\begin{eqnarray}
E{\;}{\cdot}{\;}\frac{1}{s}=RI(s)+L\left(sI(s)-i(0)\right)\tag{5}
\end{eqnarray}

(5)式において、『\(i(0)\)』は『\(t=0\)』の時におけるRL直列回路に流れる電流です。スイッチ\(SW\)をオンする前は、RL直列回路に電流は流れていないため、次式が成り立ちます。

\begin{eqnarray}
i(0)=0\tag{6}
\end{eqnarray}

(6)式を(5)式に代入すると、次式となります。

\begin{eqnarray}
E{\;}{\cdot}{\;}\frac{1}{s}&=&RI(s)+L\left(sI(s)-0\right)\\
{\Leftrightarrow}\frac{E}{s}&=&RI(s)+sLI(s)\tag{7}
\end{eqnarray}

上式が、RL直列回路のs領域の方程式となります。

【RL直列回路】s領域の方程式を解く

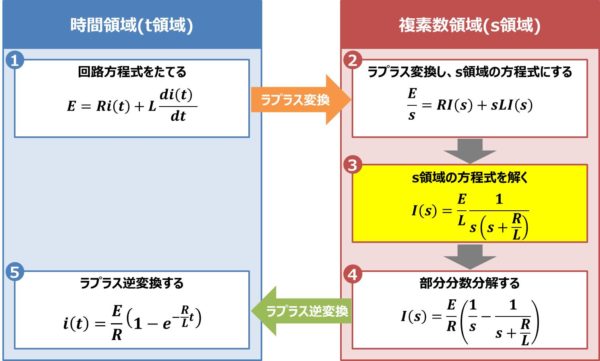
(7)式を『\(I(s)={\cdots}\)』の式に変換します。

(7)式を\(I(s)\)で整理すると、次式となります。

\begin{eqnarray}
\left(R+sL\right)I(s)=\frac{E}{s}\tag{8}
\end{eqnarray}

(8)式の両辺を\(R+sL\)で割ると次式となります。

\begin{eqnarray}
I(s)&=&\frac{E}{s\left(R+sL\right)}\\
&=&\frac{E}{s\left(sL+R\right)}\tag{9}
\end{eqnarray}

(9)式の右辺の分子と分母を\(L\)で割ると次式となります。
\begin{eqnarray}
I(s)&=&\frac{\displaystyle\frac{E}{L}}{s\left(s+\displaystyle\frac{R}{L}\right)}\\
&=&\frac{E}{L}\frac{1}{s\left(s+\displaystyle\frac{R}{L}\right)}\tag{10}
\end{eqnarray}

このように、変形することで、『\(I(s)={\cdots}\)』にすることができます。なお、(10)式はこの後に説明する部分分数分解をしやすいように変形しています。

【RL直列回路】部分分数分解する

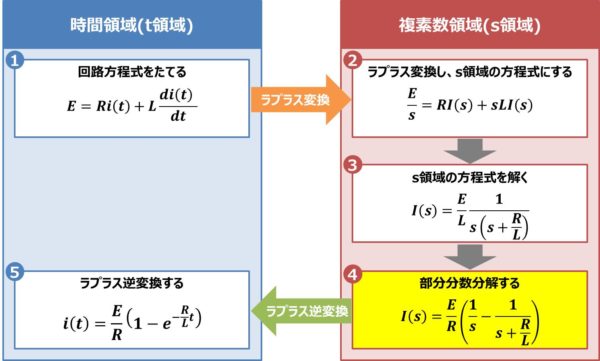
ラプラス逆変換をするために、(10)式を部分分数分解します。

まず、(10)式の右辺の\(\displaystyle\frac{1}{s\left(s+\displaystyle\frac{R}{L}\right)}\)を\(F(s)\)と置き、次式の\(A\)と\(B\)を求めます。

\begin{eqnarray}
F(s)=\frac{1}{s\left(s+\displaystyle\frac{R}{L}\right)}=\frac{A}{s}+\frac{B}{s+\displaystyle\frac{R}{L}}\tag{11}
\end{eqnarray}

Aの求め方

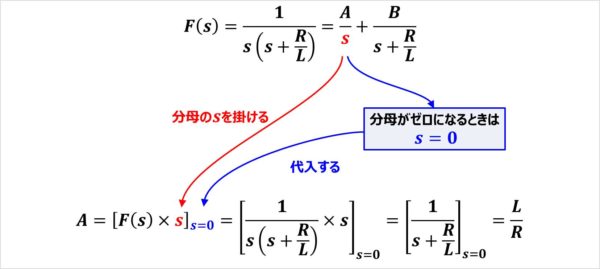
\(F(s)\)に\(A\)の分母の『\(s\)』を掛けます。その後、\(A\)の分母の『\(s\)』がゼロとなる時の条件『\(s=0\)』を代入することで\(A\)を求めることができます。

式で書くと、次式のようになります。
\begin{eqnarray}
A&=&\left[F(s)×s\right]_{s=0}\\
&=&\left[\frac{1}{s\left(s+\displaystyle\frac{R}{L}\right)}×s\right]_{s=0}\\
&=&\left[\frac{1}{s+\displaystyle\frac{R}{L}}\right]_{s=0}\\
&=&\frac{L}{R}\tag{12}
\end{eqnarray}

Bの求め方

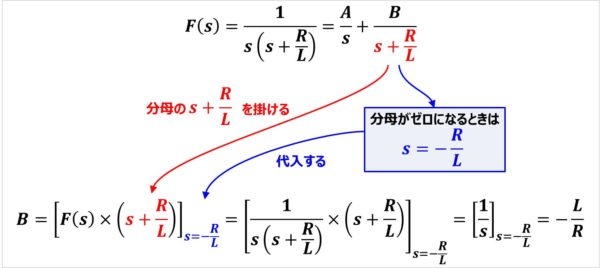
\(A\)と同様の方法で\(B\)も求めることができます。

\(F(s)\)に\(B\)の分母の『\(s+\displaystyle\frac{R}{L}\)』を掛けます。その後、\(B\)の分母の『\(s+\displaystyle\frac{R}{L}\)』がゼロとなる時の条件『\(s=-\displaystyle\frac{R}{L}\)』を代入することで\(A\)を求めることができます。

式で書くと、次式のようになります。
\begin{eqnarray}
A&=&\left[F(s)×\left(s+\displaystyle\frac{R}{L}\right)\right]_{s=-\frac{R}{L}}\\
&=&\left[\frac{1}{s\left(s+\displaystyle\frac{R}{L}\right)}×\left(s+\displaystyle\frac{R}{L}\right)\right]_{s=-\frac{R}{L}}\\
&=&\left[\frac{1}{s}\right]_{s=-\frac{R}{L}}\\
&=&-\frac{L}{R}\tag{13}
\end{eqnarray}

(12)式と(13)式を(11)式に代入すると、次式となります。

\begin{eqnarray}
\frac{1}{s\left(s+\displaystyle\frac{R}{L}\right)}&=&\frac{A}{s}+\frac{B}{s+\displaystyle\frac{R}{L}}\\
&=&\displaystyle\frac{\displaystyle\frac{L}{R}}{s}+\frac{-\displaystyle\frac{L}{R}}{s+\displaystyle\frac{R}{L}}\\
&=&\frac{L}{R}\left(\frac{1}{s}-\frac{1}{s+\displaystyle\frac{R}{L}}\right)\tag{14}
\end{eqnarray}

(14)式を(10)式に代入すると、次式となります。

\begin{eqnarray}
I(s)&=&\frac{E}{L}\frac{1}{s\left(s+\displaystyle\frac{R}{L}\right)}\\
&=&\frac{E}{L}\frac{L}{R}\left(\frac{1}{s}-\frac{1}{s+\displaystyle\frac{R}{L}}\right)\\
&=&\frac{E}{R}\left(\frac{1}{s}-\frac{1}{s+\displaystyle\frac{R}{L}}\right)\tag{15}
\end{eqnarray}

このようにして、ラプラス逆変換ができる式に変形します。

【RL直列回路】ラプラス逆変換する

(15)式をラプラス逆変換すると、次式となります。

\begin{eqnarray}
i(t)&=&{\mathcal{L}}^{-1}\left[I(s)\right]\\
&=&{\mathcal{L}}^{-1}\left[\frac{E}{R}\left(\frac{1}{s}-\frac{1}{s+\displaystyle\frac{R}{L}}\right)\right]\\
&=&\frac{E}{R}{\mathcal{L}}^{-1}\left[\frac{1}{s}-\frac{1}{s+\displaystyle\frac{R}{L}}\right]\\
&=&\frac{E}{R}\left({\mathcal{L}}^{-1}\left[\frac{1}{s}\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s+\displaystyle\frac{R}{L}}\right]\right)\\
&=&\frac{E}{R}\left(1-e^{-\frac{R}{L}t}\right)\tag{16}
\end{eqnarray}

以上より、RL直列回路に流れる電流\(i(t)\)の式を導出することができました。

RL直列回路に流れる電流\(i(t)\)が分かると、抵抗\(R\)の電圧\(v_{R}(t)\)を簡単に求めることができます。

(16)式を(2)式に代入すると、抵抗\(R\)の電圧\(v_{R}(t)\)は次式となります。

\begin{eqnarray}
v_{R}(t)&=&Ri(t)\\
&=&E\left(1-e^{-\frac{R}{L}t}\right)\tag{17}
\end{eqnarray}

また、(16)式を(3)式に代入すると、インダクタ\(L\)の電圧\(v_{L}(t)\)は次式となります。

\begin{eqnarray}
v_{L}(t)&=&L\frac{di(t)}{dt}\\
&=&L\frac{d}{dt}\left[\frac{E}{R}\left(1-e^{-\frac{R}{L}t}\right)\right]\\
&=&L\frac{E}{R}\frac{d}{dt}\left(1-e^{-\frac{R}{L}t}\right)\\
&=&L\frac{E}{R}\left[\frac{d}{dt}\left(1\right)-\frac{d}{dt}\left(e^{-\frac{R}{L}t}\right)\right]\\
&=&L\frac{E}{R}\left[0-\left(-\frac{R}{L}e^{-\frac{R}{L}t}\right)\right]\\
&=&Ee^{-\frac{R}{L}t}\tag{18}
\end{eqnarray}

なお、各々の式のグラフについては以下の記事に詳しく説明していますので、参考にしてください。