この記事ではRC直列回路の『微分方程式による過渡現象の解き方』について説明しています。
分かりやすく説明するために、図を多く用いており、式の導出過程も細かく書くように意識しています。
【RC直列回路】『過渡現象』の式とグラフ
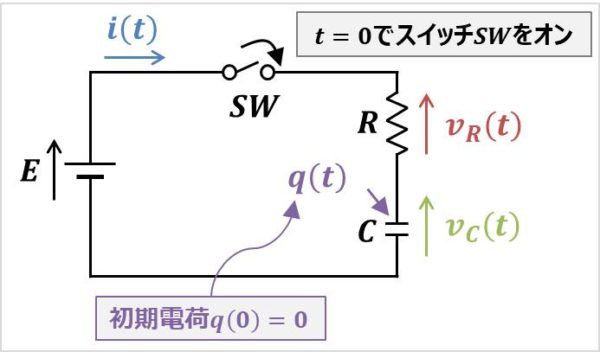
上図は抵抗\(R{\mathrm{[Ω]}}\)、コンデンサ\(C{\mathrm{[F]}}\)、直流電源\(E{\mathrm{[V]}}\)、スイッチ\(SW\)からなるRC直列回路です。
この記事では、以下の条件における『過渡現象』の式を導出します。
条件
- スイッチ\(SW\)をオンした時の時間\(t\)を\(t=0{\mathrm{[s]}}\)とする。
- スイッチ\(SW\)をオンする前には、コンデンサ\(C\)に蓄えらえている電荷\(q(t)\)はゼロとする。
→つまり、『\(q(0)=0\)』ということ。
スイッチ\(SW\)をオンすると、以下の過渡現象が生じます。
- 電流\(i(t)\)が流れて、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)が増え、コンデンサ\(C\)の電圧\(v_{C}(t)\)が上昇する。
- ある程度時間が経過すると、電流\(i(t)\)が流れなくなる(つまり、一定値\(0{\mathrm{[A]}}\)になる)。また、その時、コンデンサ\(C\)が開放されたような状態であり、コンデンサ\(C\)の電圧\(v_{C}(t)\)が電源電圧の電圧\(E\)と等しくなる。
この時、電流\(i(t)\)が一定値\(0{\mathrm{[A]}}\)となった状態を「定常状態」、「定常状態」に至るまでの状態を「過渡状態」、その過程で見られる現状を「過渡現象」といいます。
また、RC直列回路に流れる電流\(i(t)\)、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)、抵抗\(R\)の電圧\(v_{R}(t)\)、コンデンサ\(C\)の電圧\(v_{C}(t)\)の式とグラフは下記となります。
\begin{eqnarray}
i(t)&=&\frac{E}{R}e^{-\frac{1}{CR}t}\\
q(t)&=&CE\left(1-e^{-\frac{1}{CR}t}\right)\\
v_{R}(t)&=&Ee^{-\frac{1}{CR}t}\\
v_{C}(t)&=&E\left(1-e^{-\frac{1}{CR}t}\right)
\end{eqnarray}
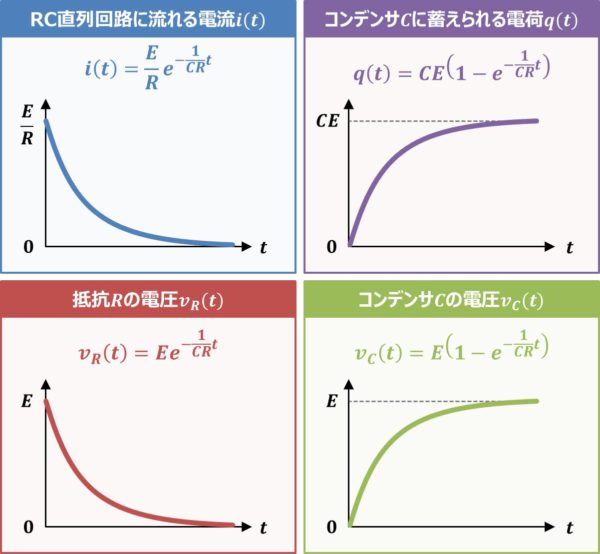
この記事では上式を微分方程式を解く最も基本的の変数分離形の微分方程式で解いていきます。なお、上式はラプラス変換でも解くことができます。
ラプラス変換で解く方法については以下の記事に詳しく説明していますので、参考にしてください。
-

【RC直列回路のラプラス変換】『過渡現象』の解き方!
続きを見る
【RC直列回路】『微分方程式』の解き方
【RC直列回路】電流i(t)の求め方
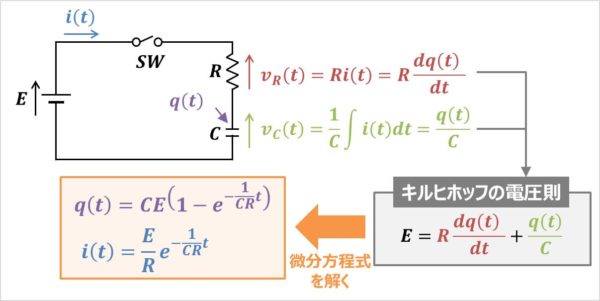

RC直列回路に流れる電流\(i(t)\)とコンデンサ\(C\)に蓄えられる電荷\(q(t)\)の関係は次式で表されます。
\begin{eqnarray}
i(t)=\frac{dq(t)}{dt}\tag{1}
\end{eqnarray}
また、RC直列回路にキルヒホッフの電圧則(キルヒホッフの第二法則)を用いると次式が成り立ちます。
\begin{eqnarray}
E=v_{R}(t)+v_{C}(t)\tag{2}
\end{eqnarray}
(2)式において、抵抗\(R\)の電圧\(v_{R}(t)\)とコンデンサ\(C\)の電圧\(v_{C}(t)\)は次式で表されます。
\begin{eqnarray}
v_{R}(t)&=&Ri(t)=R\frac{dq(t)}{dt}\tag{3}\\
v_{C}(t)&=&\frac{1}{C}{\displaystyle\int}i(t)dt=\frac{1}{C}{\displaystyle\int}\left(\frac{dq(t)}{dt}\right)dt=\frac{q(t)}{C}\tag{4}
\end{eqnarray}
(3)式と(4)式を(2)式に代入すると、次式が得られます。
\begin{eqnarray}
E&=&v_{R}(t)+v_{C}(t)\\
&=&R\frac{dq(t)}{dt}+\frac{q(t)}{C}\tag{5}
\end{eqnarray}
(5)式はコンデンサ\(C\)に蓄えられる電荷\(q(t)\)に関する「微分方程式」です。
この「微分方程式」を解くと、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)を導出することができ、次式の指数関数となります(次式の導出方法については、導出過程がかなり長くなるため、この記事の後半に詳しく説明しています)。
\begin{eqnarray}
q(t)=CE\left(1-e^{-\frac{1}{CR}t}\right)\tag{6}
\end{eqnarray}
ここで、(6)式を(1)式に代入すると、RC直列回路に流れる電流\(i(t)\)を求めることができ、次式の指数関数となります(次式の導出方法については、導出過程がかなり長くなるため、この記事の後半に詳しく説明しています)。
\begin{eqnarray}
i(t)&=&\frac{E}{R}e^{-\frac{1}{CR}t}\tag{7}
\end{eqnarray}
【RC直列回路】電流i(t)のグラフ
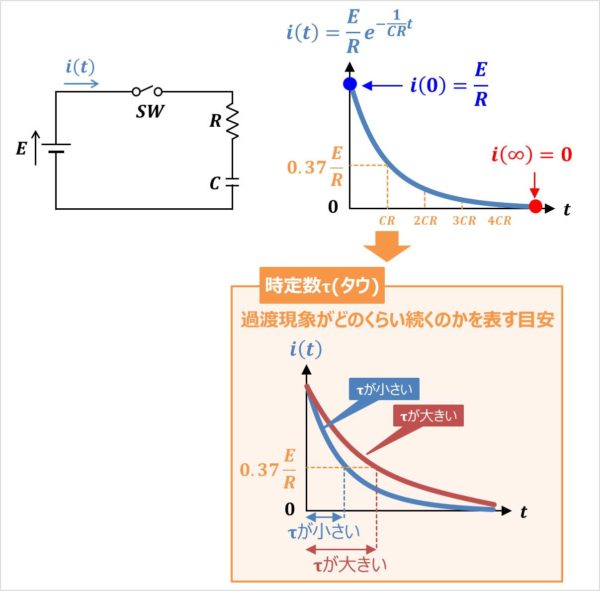

RC直列回路に流れる電流\(i(t)\)のグラフは上図のようになります。このグラフについて説明します。
繰り返しになりますが、RC直列回路に流れる電流\(i(t)\)の式は次式となります。
\begin{eqnarray}
i(t)&=&\frac{E}{R}e^{-\frac{1}{CR}t}\tag{7}
\end{eqnarray}
(7)式の\(t\)に『\(t=0\)』と『\(t=∞\)』を代入した時を考えてみましょう。
『t=0』を代入した時
『\(t=0\)』を代入すると、(7)式は次式となります。
\begin{eqnarray}
i(0)&=&\frac{E}{R}e^{-\frac{1}{CR}×0}\\
&=&\frac{E}{R}e^{0}\\
&=&\frac{E}{R}×1\\
&=&\frac{E}{R}\tag{8}
\end{eqnarray}
つまり『\(t=0\)』の時、RC直列回路に流れる電流\(i(t)\)は『\(i(0)=\displaystyle\frac{E}{R}\)』となります。
これは、スイッチ\(SW\)をオンした瞬間、コンデンサ\(C\)は短絡されたような状態であり、抵抗\(R\)によってRC直列回路に流れる電流が制限されているということを表しています。
『t=∞』を代入した時(定常状態の時)
『\(t=∞\)』を代入すると、(7)式は次式となります。
\begin{eqnarray}
i(∞)&=&\frac{E}{R}e^{-\frac{1}{CR}×∞}\\
&=&\frac{E}{R}e^{-∞}\\
&=&\frac{E}{R}\frac{1}{e^{∞}}\\
&=&\frac{E}{R}\frac{1}{∞}\\
&=&\frac{E}{R}×0\\
&=&0\tag{9}
\end{eqnarray}
つまり、『\(t=∞\)』の時、RC直列回路に流れる電流\(i(t)\)は『\(i(∞)=0\)』となります。
これは、スイッチ\(SW\)をオンし、しばらく時間が経過すると、コンデンサ\(C\)に電荷\(q(t)\)が蓄えられ、このコンデンサ\(C\)の電荷\(q(t)\)が溜まりきり、コンデンサ\(C\)の電圧\(v_{C}(t)\)が直流電源の電圧\(E\)と等しくなると、RC直列回路に流れる電流がゼロになることを表しています。
したがって、RC直列回路に流れる電流\(i(t)\)のグラフは『\(i(0)=\displaystyle\frac{E}{R}\)』から『\(i(∞)=0\)』になるように減少していくのですが、この減少具合は『コンデンサ\(C\)と抵抗\(R\)の積\(CR\)』によって変わります。
この、\(CR\)は一般的に時定数τ(タウ)と呼ばれています。
時定数τ(タウ)は過渡現象がどのくらい続くのかを表す目安を表しており、単位は[s]となります。
今回のRC直列回路に流れる電流\(i(t)\)のグラフの場合、『\({\tau}=CR\)』の大きさによって以下のように変わります。
- 『\({\tau}=CR\)』が大きい時
- 『\({\tau}=CR\)』が小さい時
過渡現象が長く続きます。
過渡現象が早く終わります。すなわち、早く定常状態となります。
また、時間tが時定数τ(タウ)と等しくなる時、RC直列回路に流れる電流\(i(t)\)は以下の値となります。
- 『\(t={\tau}=CR\)』の時
- 『\(t=4{\tau}=4CR\)』の時
『\(\displaystyle\frac{E}{R}\)』の約37%
『\(\displaystyle\frac{E}{R}\)』の約2%
【RC直列回路】コンデンサCに蓄えられる電荷q(t)のグラフ
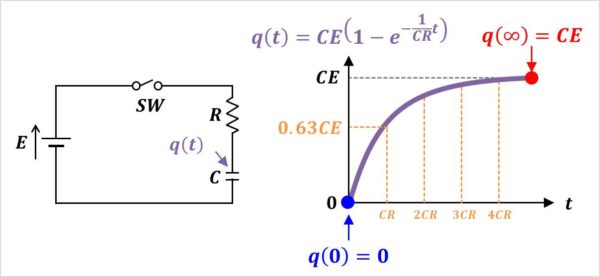

コンデンサ\(C\)に蓄えられる電荷\(q(t)\)のグラフは上図のようになります。このグラフについて説明します。
繰り返しになりますが、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)の式は次式となります。
\begin{eqnarray}
q(t)=CE\left(1-e^{-\frac{1}{CR}t}\right)\tag{6}
\end{eqnarray}
(6)式の\(t\)に『\(t=0\)』と『\(t=∞\)』を代入した時を考えてみましょう。
『t=0』を代入した時
『\(t=0\)』を代入すると、(6)式は次式となります。
\begin{eqnarray}
q(0)&=&CE\left(1-e^{-\frac{1}{CR}×0}\right)\\
&=&CE\left(1-e^{0}\right)\\
&=&CE\left(1-1\right)\\
&=&0\tag{10}
\end{eqnarray}
つまり『\(t=0\)』の時、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)は『\(q(0)=0\)』となります。
これは、スイッチ\(SW\)をオンした瞬間、コンデンサ\(C\)に蓄えられている電荷はゼロであるということを表しています。
『t=∞』を代入した時(定常状態の時)
『\(t=∞\)』を代入すると、(6)式は次式となります。
\begin{eqnarray}
q(∞)&=&CE\left(1-e^{-\frac{1}{CR}×∞}\right)\\
&=&CE\left(1-e^{-∞}\right)\\
&=&CE\left(1-\frac{1}{e^{∞}}\right)\\
&=&CE\left(1-0\right)\\
&=&CE\tag{11}
\end{eqnarray}
つまり、『\(t=∞\)』の時、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)は『\(q(∞)=CE\)』となります。
これは、スイッチ\(SW\)をオンし、しばらく時間が経過すると、コンデンサ\(C\)に電荷\(q(t)\)が蓄えられ、このコンデンサ\(C\)の電荷\(q(t)\)が溜まりきり、コンデンサ\(C\)の電圧\(v_{C}(t)\)が直流電源の電圧\(E\)と等しくなると、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)が\(CE\)になることを表しています。
したがって、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)のグラフは『\(q(0)=0\)』から『\(q(∞)=CE\)』になるように増加していくのですが、この増加具合は時定数τ(タウ)によって変わります。
また、時間tが時定数τ(タウ)と等しくなる時、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)は以下の値となります。
- 『\(t={\tau}=CR\)』の時
- 『\(t=4{\tau}=4CR\)』の時
『\(CE\)』の約63%
『\(CE\)』の約98%
また、定常状態において、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)が変化しないということは、(7)式より、RC直列回路に流れる電流\(i(t)\)がゼロということになります。各々のグラフを見るとそのようになっていることが確認できると思います。
【RC直列回路】抵抗Rの電圧VR(t)の求め方
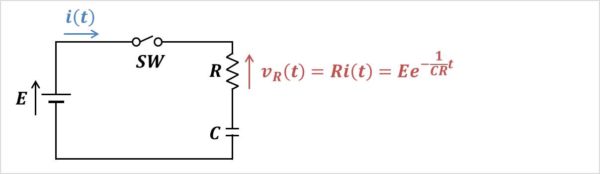

RC直列回路に流れる電流\(i(t)\)が分かると、抵抗\(R\)の電圧\(v_{R}(t)\)を簡単に求めることができます。
(7)式を(3)式に代入すると、抵抗\(R\)の電圧\(v_{R}(t)\)は次式となります。
\begin{eqnarray}
v_{R}(t)&=&Ri(t)\\
&=&E{\;}e^{-\frac{1}{CR}t}\tag{12}
\end{eqnarray}
【RC直列回路】抵抗Rの電圧VR(t)のグラフ
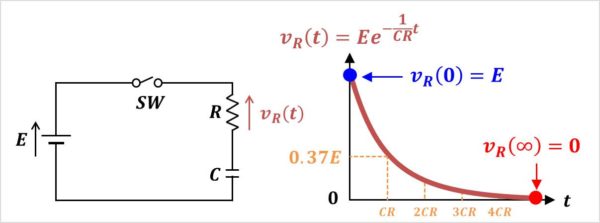

抵抗\(R\)の電圧\(v_{R}(t)\)のグラフは上図のようになります。このグラフについて説明します。
このグラフですが、抵抗\(R\)の電圧\(v_{R}(t)\)はRC直列回路に流れる電流\(i(t)\)に\(R\)を掛けただけです。
すなわち、RC直列回路に流れる電流\(i(t)\)のグラフと同じようなグラフとなります。
スイッチ\(SW\)をオンした瞬間、コンデンサ\(C\)は短絡されたような状態であるため、抵抗\(R\)に直流電源の電圧\(E\)がかかります。
スイッチ\(SW\)をオンし、しばらく時間が経過すると(定常状態の時)、RC直列回路に流れる電流\(i(t)\)がゼロなので、抵抗\(R\)の電圧\(v_{R}(t)\)もゼロとなります。
【RC直列回路】コンデンサCの電圧VC(t)の求め方
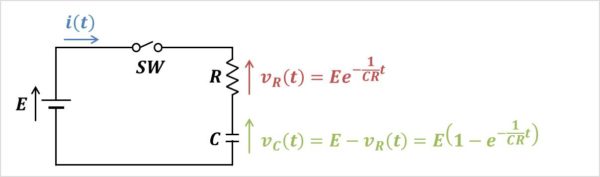

コンデンサ\(C\)の電圧\(v_{C}(t)\)はキルヒホッフの電圧則(キルヒホッフの第二法則)を用いると簡単に求めることができます。
(2)式を変形すると、次式となります。
\begin{eqnarray}
&&E=v_{R}(t)+v_{C}(t)\\
{\Leftrightarrow}&&v_{C}(t)=E-v_{R}(t)\tag{13}
\end{eqnarray}
(13)式に(12)式を代入すると、コンデンサ\(C\)の電圧\(v_{C}(t)\)は次式となります。
\begin{eqnarray}
v_{C}(t)&=&E-v_{R}(t)\\
&=&E-E{\;}e^{-\frac{1}{CR}t}\\
&=&E\left(1-e^{-\frac{1}{CR}t}\right)\tag{14}
\end{eqnarray}
【RC直列回路】コンデンサCの電圧VC(t)のグラフ
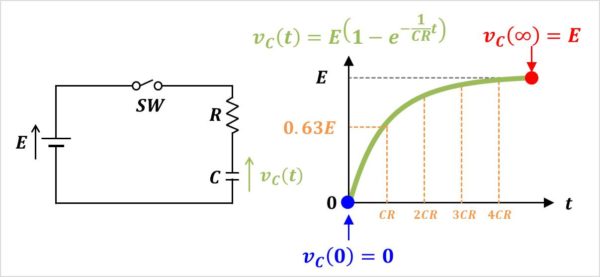

コンデンサ\(C\)の電圧\(v_{C}(t)\)のグラフは上図のようになります。このグラフについて説明します。
このグラフですが、コンデンサ\(C\)の電圧\(v_{C}(t)\)はコンデンサ\(C\)に蓄えられる電荷\(q(t)\)に\(\displaystyle\frac{1}{C}\)を掛けただけです。
すなわち、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)のグラフと同じようなグラフとなります。
スイッチ\(SW\)をオンした瞬間、コンデンサ\(C\)は短絡されたような状態であるため、コンデンサ\(C\)の電圧はゼロとなります。
スイッチ\(SW\)をオンし、しばらく時間が経過すると(定常状態の時)、コンデンサ\(C\)に電荷\(q(t)\)が蓄えられ、このコンデンサ\(C\)の電荷\(q(t)\)が溜まりきり、コンデンサ\(C\)の電圧\(v_{C}(t)\)が直流電源の電圧\(E\)と等しくなります。
『微分方程式』の解き方
繰り返しになりますが、(5)式と(6)式をもう一度示します。
(5)式はコンデンサ\(C\)に蓄えられる電荷\(q(t)\)に関する「微分方程式」となり次式となります。
\begin{eqnarray}
E=R\frac{dq(t)}{dt}+\frac{q(t)}{C}\tag{5}
\end{eqnarray}
この「微分方程式」を解くと、(6)式のコンデンサ\(C\)に蓄えられる電荷\(q(t)\)を導出することができます。
\begin{eqnarray}
q(t)=CE\left(1-e^{-\frac{1}{CR}t}\right)\tag{6}
\end{eqnarray}
この導出方法について説明します。
導出方法
ここでは、微分方程式を解く最も基本的なパターンの一つである『変数分離形の微分方程式』で解いていきます。
『変数分離形の微分方程式』とはその名の通り、変数を左辺と右辺に分離した微分方程式のことです。
(5)式の場合、電荷\(q(t)\)と時間\(t\)が変数なので、電荷\(q(t)\)に関するものを左辺に、時間\(t\)に関するものを右辺になるように分離します。
すなわち、(5)式を次式の形になるように変形します。
\begin{eqnarray}
□dq(t)=□dt\tag{15}
\end{eqnarray}
変形は以下のように行います。
変数を左辺と右辺に分離する方法
まず、(5)式の\(R\displaystyle\frac{dq(t)}{dt}\)を左辺に、\(E\)を右辺に移動して、両辺にマイナスを掛けると、次式となります。
\begin{eqnarray}
R\frac{dq(t)}{dt}=\frac{CE-q(t)}{C}\tag{16}
\end{eqnarray}
(16)式の両辺を\(R\)で割ると、次式となります。
\begin{eqnarray}
\frac{dq(t)}{dt}=\frac{CE-q(t)}{CR}\tag{17}
\end{eqnarray}
(17)式の両辺を\(CE-q(t)\)で割ると、次式となります。
\begin{eqnarray}
\frac{1}{CE-q(t)}\frac{dq(t)}{dt}=\frac{1}{CR}\tag{18}
\end{eqnarray}
(18)式の両辺に\(dt\)を掛けると、次式となります。
\begin{eqnarray}
\frac{1}{CE-q(t)}dq(t)=\frac{1}{CR}dt\tag{19}
\end{eqnarray}
以上より、電荷\(q(t)\)に関するものを左辺に、時間\(t\)に関するものを右辺になるように分離できました。
すなわち、『\(□dq(t)=□dt\)』の形になるように変形することができました。なお、コンデンサ\(C\)と抵抗\(R\)と直流電源の電圧\(E\)は定数なので、左辺にあっても右辺にあってもどっちでも良いです。
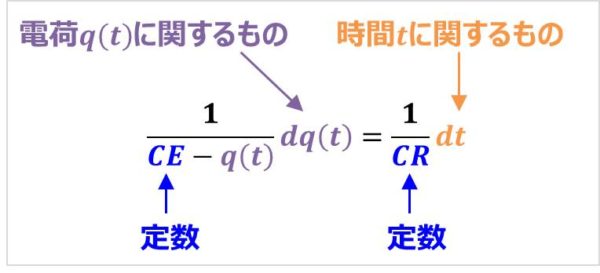

(19)式の両辺を積分すると、次式となります。
\begin{eqnarray}
{\displaystyle\int}\frac{1}{CE-q(t)}dq(t)={\displaystyle\int}\frac{1}{CR}dt\tag{20}
\end{eqnarray}
(20)式の左辺と右辺は別々に解いていきます。
左辺の解き方
『\(k=CE-q(t)\)』と置くと、\(q(t)\)はコンデンサ\(C\)に蓄えられていく電荷であり、\(CE\)は定常状態においてコンデンサ\(C\)に蓄えられている電荷なので、『\(k=CE-q(t){≥}0\)』となります。
また、『\(dk=-dq(t)\)』となるので、(20)式の左辺は次式のように変形できます。
\begin{eqnarray}
(20)式の左辺&=&{\displaystyle\int}\frac{1}{CE-q(t)}dq(t)\\
&=&-{\displaystyle\int}\frac{1}{k}dk\\
&=&-\log_{e}k+A\\
&=&-\log_{e}\left(CE-q(t)\right)+A\tag{21}
\end{eqnarray}
(21)式において、\(A\)は積分定数となっています。
右辺の解き方
\(\displaystyle\frac{1}{CR}\)は定数なので、積分の外に出すことができるので、(20)式の右辺は次式のように変形できます。
\begin{eqnarray}
(20)式の右辺&=&{\displaystyle\int}\frac{1}{CR}dt\\
&=&\frac{1}{CR}{\displaystyle\int}dt\\
&=&\frac{1}{CR}t+B\tag{22}
\end{eqnarray}
(22)式において、\(B\)は積分定数となっています。
(21)式と(22)式を(20)式に戻すと、次式となります。
\begin{eqnarray}
-\log_{e}\left(CE-q(t)\right)+A=\frac{1}{CR}t+B\tag{23}
\end{eqnarray}
(23)式では\(A\)と\(B\)の2つの積分定数があります。そこで、\(A-B=D\)と置くと、(23)式は次式のように変形できます。
\begin{eqnarray}
\log_{e}\left(CE-q(t)\right)=-\frac{1}{CR}t+D\tag{24}
\end{eqnarray}
(24)式を変形すると、次式となります。
\begin{eqnarray}
CE-q(t)&=&e^{-\frac{1}{CR}t+D}\\
&=&e^{-\frac{1}{CR}t}×e^{D}\tag{25}
\end{eqnarray}
(25)式において、\(CE\)を右辺に移動して、両辺にマイナスを掛けると、次式となります。
\begin{eqnarray}
q(t)=CE-e^{-\frac{1}{CR}t}×e^{D}\tag{26}
\end{eqnarray}
次に、(26)式の積分定数\(D\)を求める必要があります。
積分定数\(D\)は以下のように求めます。
積分定数Dの求め方
積分定数は回路の初期条件を用いることで求めることができます。
この回路の場合、『\(t=0\)』の時、すなわち、スイッチ\(SW\)をオンした瞬間は、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)はゼロとなります。
そのため、初期条件は『\(t=0、q(0)=0\)』となります。
(26)式に初期条件を代入すると、
\begin{eqnarray}
q(0)&=&CE-e^{-\frac{1}{CR}×0}×e^{D}\\
{\Leftrightarrow}0&=&CE-e^0×e^{D}\\
0&=&CE-1×e^{D}\\
0&=&CE-e^{D}\tag{27}
\end{eqnarray}
となります。
つまり、『\(t=0\)』の時、『\(e^{D}=CE\)』となります。なお、積分定数\(D\)を求めても良いですが、(26)式において、『\(e^{D}\)』をそのまま代入できます。
そのため、今回は『\(e^{D}=CE\)』までの導出で大丈夫です。
(27)式を(26)式に代入すると、次式となり、コンデンサ\(C\)に蓄えられる電荷\(q(t)\)を導出することができました。
\begin{eqnarray}
q(t)&=&CE-e^{-\frac{1}{CR}t}×e^{D}\\
&=&CE-e^{-\frac{1}{CR}t}×CE\\
&=&CE\left(1-e^{-\frac{1}{CR}t}\right)\\
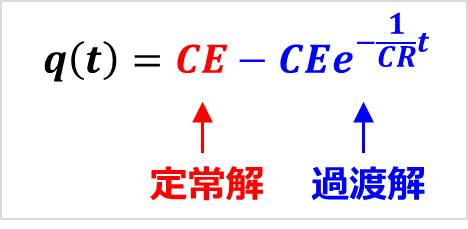
&=&CE-CEe^{-\frac{1}{CR}t}\tag{28}
\end{eqnarray}
なお、(28)式の右辺の第1項は定常解、第2項は過渡解と呼ばれています。

RC直列回路に流れる電流i(t)の導出方法
繰り返しになりますが、(1)式と(6)式と(7)式をもう一度示します。
(1)式はRC直列回路に流れる電流\(i(t)\)とコンデンサ\(C\)に蓄えられる電荷\(q(t)\)の関係であり、次式で表されます。
\begin{eqnarray}
i(t)=\frac{dq(t)}{dt}\tag{1}
\end{eqnarray}
(6)式はコンデンサ\(C\)に蓄えられる電荷\(q(t)\)であり、次式となります。
\begin{eqnarray}
q(t)=CE\left(1-e^{-\frac{1}{CR}t}\right)\tag{6}
\end{eqnarray}
ここで、(6)式を(1)式に代入すると、RC直列回路に流れる電流\(i(t)\)を求めることができ、次式の指数関数となります
\begin{eqnarray}
i(t)&=&\frac{E}{R}e^{-\frac{1}{CR}t}\tag{7}
\end{eqnarray}
この導出方法について説明します。
導出方法
(6)式を(1)式に代入すると、次式となります。
\begin{eqnarray}
i(t)=\frac{d}{dt}CE\left(1-e^{-\frac{1}{CR}t}\right)\tag{29}
\end{eqnarray}
ここで、\(CE\)は定数なので、微分の外に出すと次式となります。
\begin{eqnarray}
i(t)&=&CE\frac{d}{dt}\left(1-e^{-\frac{1}{CR}t}\right)\\
&=&CE\left(\frac{d}{dt}1-\frac{d}{dt}e^{-\frac{1}{CR}t}\right)\\
&=&CE\left\{0-\left(-\frac{1}{CR}e^{-\frac{1}{CR}t}\right)\right\}\\
&=&CE\left(\frac{1}{CR}e^{-\frac{1}{CR}t}\right)\\
&=&\frac{E}{R}e^{-\frac{1}{CR}t}\tag{30}
\end{eqnarray}
以上より、RC直列回路に流れる電流\(i(t)\)を求めることができました。
補足
- 時定数\({\tau}=CR\)の単位がなぜ\({\mathrm{[s]}}\)なのか
コンデンサ\(C\)の単位は
\begin{eqnarray}
\frac{{\mathrm{[C]}}}{{\mathrm{[V]}}}=\frac{{\mathrm{[A]}}{\mathrm{[s]}}}{{\mathrm{[V]}}}
\end{eqnarray}
となります。
抵抗\(R\)の単位は
\begin{eqnarray}
\frac{{\mathrm{[V]}}}{{\mathrm{[A]}}}
\end{eqnarray}
となります。
したがって、時定数\({\tau}=CR\)の単位は
\begin{eqnarray}
\frac{{\mathrm{[A]}}{\mathrm{[s]}}}{{\mathrm{[V]}}}×\frac{{\mathrm{[V]}}}{{\mathrm{[A]}}}={\mathrm{[s]}}
\end{eqnarray}
となります。
まとめ
この記事ではRC直列回路について、以下の内容を説明しました。
当記事のまとめ
- 【RC直列回路】『過渡現象』の式とグラフ
- 【RC直列回路】『微分方程式』の解き方
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。







