『鉄損』と『銅損』が等しい時に効率が最大となる理由

この記事では『鉄損』と『銅損』が等しい時に効率が最大となる理由について図を用いて説明しています。

『鉄損』と『銅損』が等しい時に効率が最大となる理由

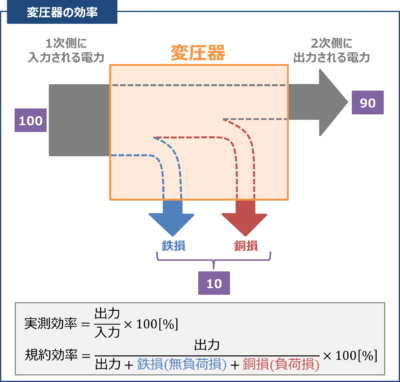
変圧器には鉄損や銅損などの損失があるため、上図に示すように、1次側に入力される電力がすべて2次側に出力されることはありません。

1次側に入力される電力に対して、どれくらい2次側に出力されるのかを表すパラメータとして効率があります。

例えば、効率が90%の場合、100のエネルギーを入力しても、出力には90のエネルギーしか出力されず、残りの10は銅損や鉄損などの損失になるというイメージです。

また、変圧器の効率には「入力と出力の測定値を用いて計算する実測効率」と「出力と損失を基準として計算する規約効率」というものがあり、以下の式で表されます。通常、変圧器では後者の規約効率を用いています。

変圧器の効率

\begin{eqnarray}
実測効率&=&\frac{出力}{入力}×100{\mathrm{[{\%}]}}\tag{1}\\
規約効率&=&\frac{出力}{出力+損失}×100{\mathrm{[{\%}]}}\\
&=&\frac{出力}{出力+鉄損(無負荷損)+銅損(負荷損)}×100{\mathrm{[{\%}]}}\tag{2}
\end{eqnarray}

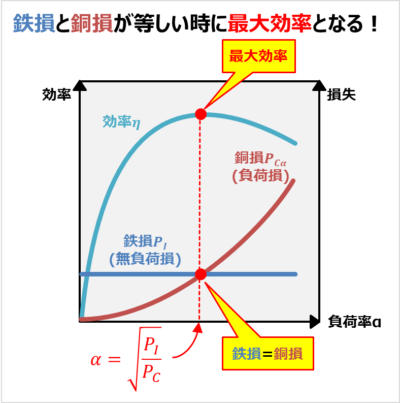
(2)式において、この時、「鉄損(無負荷損)」と「銅損(負荷損)」が等しい時に効率が最大となります。この記事ではこの理由について説明しています。

実測効率を計算する場合、入力電力と出力電力を測定する必要があります。その際、変圧器の容量が大きくなると、それに応じた電源設備を必要とするため、実測効率ではなく、規約効率を用いています。

鉄損(無負荷損)について

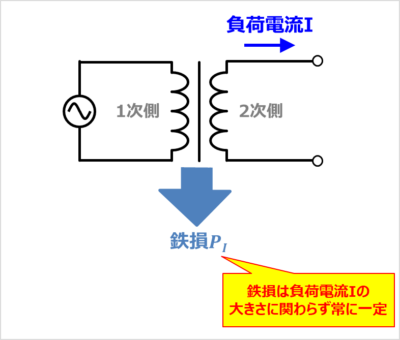
(2)式の鉄損(無負荷損)、銅損(負荷損)、出力について順番に説明していきます。まず、鉄損(無負荷損)から説明します。

鉄損(無負荷損)\(P_I\)は一定周波数の電源電圧が一次側に印加されている限り、二次側の負荷電流\(I\)の大きさに関わらず常に一定となります。

銅損(負荷損)について

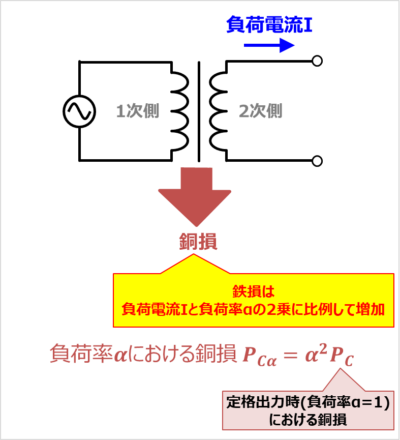
定格出力時における銅損(負荷損)\(P_C\)は定格電流を\(I_N\)、変圧器の巻線抵抗を\(R\)とすると次式で表されます。

\begin{eqnarray}
定格出力時における銅損(負荷損)P_C=R{I_N}^2\tag{3}
\end{eqnarray}

\(P_C\)は全負荷損とも呼ばれています。

(3)式より、銅損は変圧器に流れている電流の2乗に比例して増加します。また、負荷率\({\alpha}\)は負荷電流\(I\)に比例します。すなわち、銅損は負荷率\({\alpha}\)の2乗に比例して増加します。

そのため、負荷率\({\alpha}\)における銅損(負荷損)\(P_{C{\alpha}}\)は次式で表すことができます。なお、定格出力時は負荷率\({\alpha}\)が1となります。

\begin{eqnarray}
負荷率{\alpha}における銅損(負荷損)P_{C{\alpha}}={\alpha}^2P_C\tag{4}
\end{eqnarray}

負荷率αとは

負荷率\({\alpha}\)は変圧器の定格容量\({\mathrm{[kVA]}}\)に対する負荷の皮相電力\({\mathrm{[kVA]}}\)の割合のことを指します。例えば、定格容量\(200{\mathrm{[kVA]}}\)の変圧器に対して、負荷の皮相電力が\(100{\mathrm{[kVA]}}\)だった場合、負荷率\({\alpha}\)は

\begin{eqnarray}
負荷率{\alpha}=\frac{負荷の皮相電力}{変圧器の定格容量}=\frac{100{\mathrm{[kVA]}}}{200{\mathrm{[kVA]}}}=0.5\tag{5}
\end{eqnarray}

となります。

変圧器の出力について

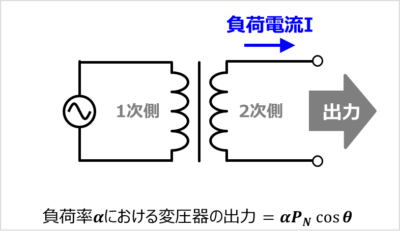
定格容量\(P_N{\mathrm{[kVA]}}\)の変圧器が力率\({\cos}{\theta}\)で運転している時、変圧器の定格出力は以下の式で表されます。

\begin{eqnarray}
変圧器の定格出力=P_N{\cos}{\theta}{\mathrm{[kW]}}\tag{6}
\end{eqnarray}

(6)式より、変圧器の出力は負荷電流\(I\)に比例します。また、負荷率\({\alpha}\)は負荷電流\(I\)に比例します。すなわち、変圧器の出力は負荷率\({\alpha}\)に比例して増加します。

そのため、負荷率\({\alpha}\)における変圧器の出力は次式で表すことができます。

\begin{eqnarray}
負荷率{\alpha}における変圧器の出力={\alpha}P_N{\cos}{\theta}{\mathrm{[kW]}}\tag{7}
\end{eqnarray}

変圧器の規約効率

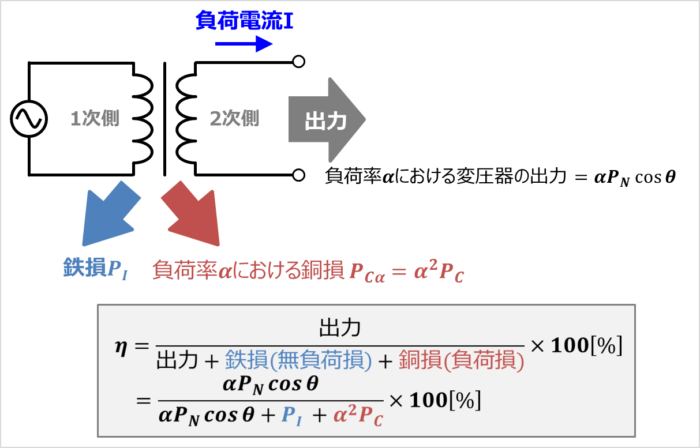
定格容量\(P_N\)、鉄損(無負荷損)\(P_I\)、銅損(全負荷損)\(P_C\)の変圧器が負荷率\({\alpha}\)、力率\({\cos}{\theta}\)で運転している時の効率(規約効率)\({\eta}\)は次式で表すことができます。

\begin{eqnarray}
{\eta}&=&\frac{出力}{出力+鉄損(無負荷損)+銅損(負荷損)}×100{\mathrm{[{\%}]}}\\
&=&\frac{{\alpha}P_N{\cos}{\theta}}{{\alpha}P_N{\cos}{\theta}+P_I+{\alpha}^2P_C}×100{\mathrm{[{\%}]}}\tag{8}
\end{eqnarray}

ここで、(8)式において、効率\({\eta}\)が最大となる負荷率\({\alpha}\)を求めてみます。

負荷率\({\alpha}\)が分母と分子にあるため、分母と分子を負荷率\({\alpha}\)で割ることで分母のみに負荷率\({\alpha}\)を持っていきます。すると、(8)式は以下の式に変形することができます。

\begin{eqnarray}
{\eta}&=&\frac{P_N{\cos}{\theta}}{P_N{\cos}{\theta}+\displaystyle\frac{1}{{\alpha}}P_I+{\alpha}P_C}×100{\mathrm{[{\%}]}}\tag{9}
\end{eqnarray}

(9)式において、\(P_N{\cos}{\theta}\)は一定値なので、効率\({\eta}\)が最大となるのは「分母が最小となるとき」となります。

この「分母が最小となるとき」の条件は「最小の定理」を用いることで求めることができます。

最小の定理とは

最小の定理は「2つの数AとBがあり、積(A×B)が一定ならば、2つの数が等しい時(A=B)に、その和(A+B)が最小である」ということを示した定理です。

ここで、(9)式の分母において「\(\displaystyle\frac{1}{{\alpha}}P_I\)」と「\({\alpha}P_C\)」の積は以下の値となり、負荷率\({\alpha}\)が消えて一定値となります。

\begin{eqnarray}
\displaystyle\frac{1}{{\alpha}}P_I×{\alpha}P_C=P_IP_C\tag{10}
\end{eqnarray}

そのため、「最小の定理」を用いることができ、以下の条件の時に「\(\displaystyle\frac{1}{{\alpha}}P_I\)」と「\({\alpha}P_C\)」の和が最小となります。すなわち、鉄損と銅損が等しい時に最大効率となります。

\begin{eqnarray}
\displaystyle\frac{1}{{\alpha}}P_I&=&{\alpha}P_C\\
{\Leftrightarrow}P_I&=&{\alpha}^2P_C\\
{\Leftrightarrow}鉄損&=&負荷率{\alpha}における銅損\tag{11}
\end{eqnarray}

また、効率\({\eta}\)が最大となるときの負荷率\({\alpha}\)は以下の式となります。

\begin{eqnarray}
P_I&=&{\alpha}^2P_C\\
{\Leftrightarrow}{\alpha}&=&\sqrt{\displaystyle\frac{P_I}{P_C}}\tag{12}
\end{eqnarray}

一般的に変圧器は負荷率\({\alpha}\)が0.5～0.75の時に最大効率となるように設計されていることが多くなっています。