この記事では『インバーテッド・ダーリントントランジスタ』について
- 『インバーテッド・ダーリントントランジスタ』とは
- 『インバーテッド・ダーリントントランジスタ』の接続と特徴
- 『電流増幅率hFEの導出方法
などを図を用いて分かりやすく説明しています。
インバーテッド・ダーリントントランジスタとは?

ダーリントントランジスタには上図に示すように、
同極性のトランジスタを組み合わせのもの
- 『1つ目:NPN型』、『2つ目:NPN型』
- 『1つ目:PNP型』、『2つ目:PNP型』
→トランジスタを1つとして考えるとNPNトランジスタとなる。
→トランジスタを1つとして考えるとPNPトランジスタとなる。
異極性のトランジスタを組み合わせたもの
- 『1つ目:NPN型』、『2つ目:PNP型』
- 『1つ目:PNP型』、『2つ目:NPN型』
→トランジスタを1つとして考えるとNPNトランジスタとなる。
→トランジスタを1つとして考えるとPNPトランジスタとなる。
があります。
通常、ダーリントントランジスタといえば同極性のトランジスタを組み合わせのものになります。
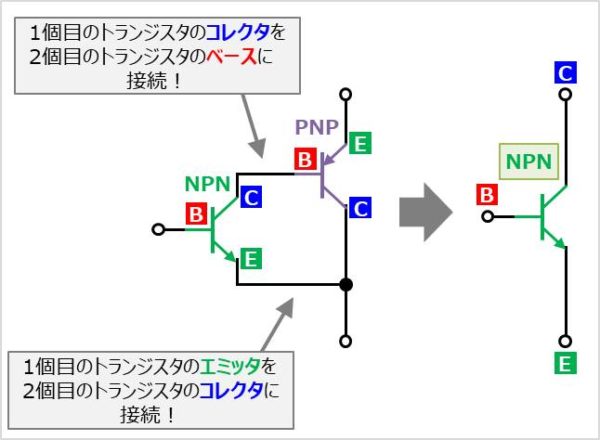
それに対して、異極性のトランジスタを組み合わせたものを『インバーテッド・ダーリントントランジスタ』と呼びます。トランジスタを1つとして考えた場合は、1つ目のトランジスタの極性と同じになります。
インバーテッド・ダーリントントランジスタでは、1つ目のコレクタ(C)を2つ目のベース(B)に接続、1つ目のエミッタ(E) を2つ目のコレクタ(C)に接続しています。
トランジスタを1つとして考えると、
- 極性が2つ目のトランジスタと逆になる点
- エミッタ(E)が2つ目のトランジスタのコレクタ(C)に相当する点
より、通常のダーリントントランジスタと比較すると、少し困惑しやすい回路となっています。
なお、通常のダーリントントランジスタについては以下の記事に記載しているので参考にしてください。
インバーテッド・ダーリントントランジスタの特徴
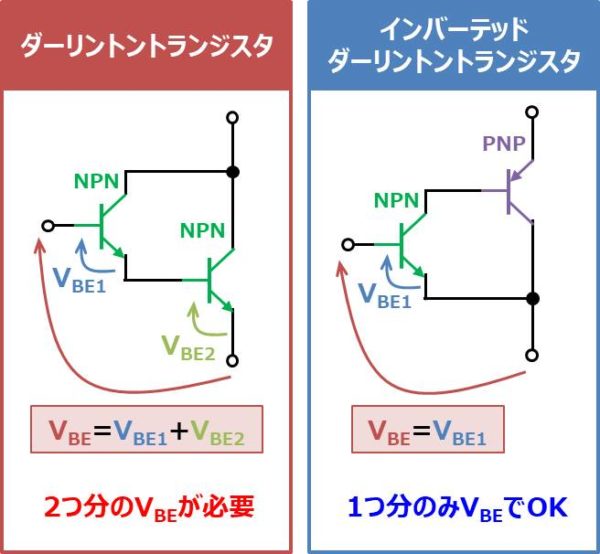

インバーテッド・ダーリントントランジスタの大きな特徴は以下のようにベースエミッタ間電圧VBEが小さいことです。
- 通常のダーリントントランジスタ
- インバーテッド・ダーリントントランジスタ
ベースエミッタ間電圧VBEが大きく、2個のトランジスタのベースエミッタ間電圧の和となります(VBE=VBE1+VBE2)。
ベースエミッタ間電圧VBEが小さく、1つ目のトランジスタのベースエミッタ間電圧となります(VBE=VBE1)。
また、インバーテッド・ダーリントントランジスタは、その他に以下の特徴を持っています。
- 電流増幅率は通常のダーリントントランジスタと同様
- コレクタエミッタ間電圧VCEが大きい
- スイッチング時間が長くなる
1個目のトランジスタ電流増幅率をhFE1、2個目のトランジスタの電流増幅率をhFE2とすると、インバーテッド・ダーリントントランジスタの電流増幅率hFEは『hFE=hFE1×hFE2』となります。
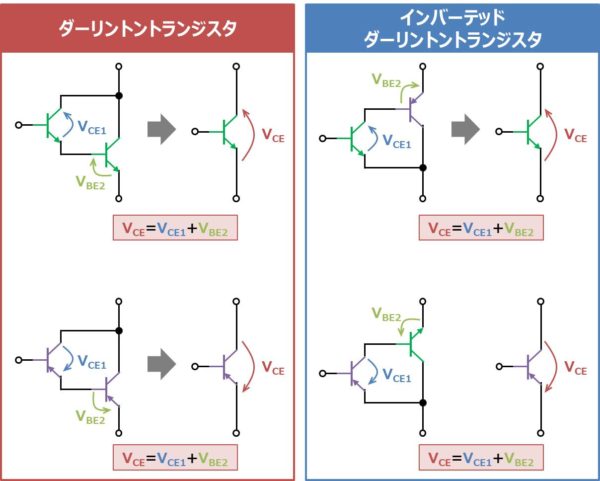
コレクタエミッタ間電圧VCEは1個目のトランジスタのコレクタエミッタ間電圧VCE1と2個目のトランジスタのベースエミッタ間電圧VBE2の和となります(VCE=VCE1+VBE2)。

補足
- インバーテッド・ダーリントントランジスタは「準トランジスタ」や「Sziklai Pair」や「Complementary Darlington」とも呼ばれています。
- インバーテッド・ダーリントントランジスタは米国に移住したハンガリーのエンジニアであるジョージ・シクライ(George Sziklai)によって発明されました。インバーテッド・ダーリントントランジスタ(Sziklai Pair)の由来は発明者の名前となっています。
電流増幅率hFEの導出方法
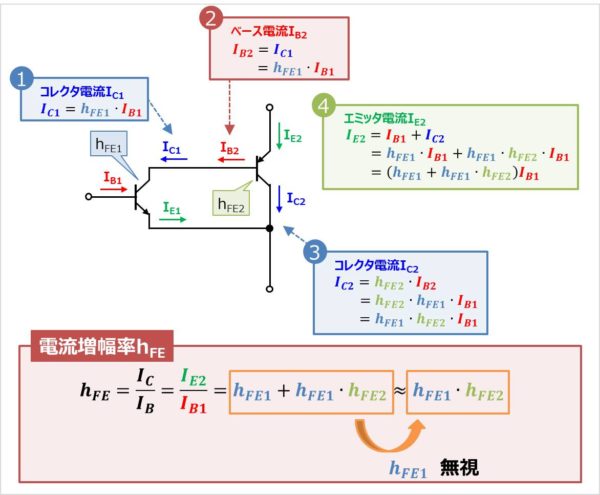

ダーリントントランジスタの電流増幅率hFEはそれぞれのトランジスタの電流増幅率(hFE1とhFE2)を掛け算した値となりますが、それを実際に導出してみましょう。
上図に示すように
- 1個目のトランジスタ
- 2個目のトランジスタ
電流増幅率をhFE1、ベース電流をIB1、コレクタ電流をIC1、エミッタ電流をIE1とします。
電流増幅率をhFE2、ベース電流をIB2、コレクタ電流をIC2、エミッタ電流をIE2とします。
として導出を行います。
1個目のトランジスタのコレクタ電流IC1は次式となります。
\begin{eqnarray}
I_{C1}=h_{FE1}{\cdot}I_{B1}
\end{eqnarray}
2個目のトランジスタのベース電流IB2は1個目のトランジスタのコレクタ電流IC1と等しいため次式となります。
\begin{eqnarray}
I_{B2}=I_{C1}=h_{FE1}{\cdot}I_{B1}
\end{eqnarray}
2個目のトランジスタのコレクタ電流IC2は次式となります。
\begin{eqnarray}
I_{C2}=h_{FE2}{\cdot}I_{B2}=h_{FE2}{\cdot}h_{FE1}{\cdot}I_{B1}=h_{FE1}{\cdot}h_{FE2}{\cdot}I_{B1}
\end{eqnarray}
2個目のトランジスタのエミッタ電流IE2はベース電流IB2とコレクタ電流IC2の足し算となるため次式となります。
\begin{eqnarray}
I_{E2}=&=&I_{B2}+I_{C2}\\
&=&h_{FE1}{\cdot}I_{B1}+h_{FE1}{\cdot}h_{FE2}{\cdot}I_{B1}\\
&=&(h_{FE1}+h_{FE1}{\cdot}h_{FE2})I_{B1}
\end{eqnarray}
ここで、インバーテッド・ダーリントントランジスタのコレクタ電流ICは2個目のトランジスタのエミッタ電流IE2と同じであり、インバーテッド・ダーリントントランジスタのベース電流IBは1個目のトランジスタのベース電流IB1と同じになります。すなわち、インバーテッド・ダーリントントランジスタの電流増幅率hFEは
インバーテッド・ダーリントントランジスタの電流増幅率
h_{FE}&=&\frac{I_{C}}{I_{B}}\\
&=&\frac{I_{E2}}{I_{B1}}\\
&=&h_{FE1}+h_{FE1}{\cdot}h_{FE2}
\end{eqnarray}
となります。
ここで、hFE1はhFE1・hFE2よりはるかに小さいため無視すると、ダーリントントランジスタの電流増幅率hFEは
インバーテッド・ダーリントントランジスタの電流増幅率
h_{FE}=h_{FE1}{\cdot}h_{FE2}
\end{eqnarray}
となります。
ここで、通常のダーリントントランジスタの電流増幅率hFEは厳密には以下となります。そのため、通常のトランジスタとインバーテッド・ダーリントントランジスタではわずかに電流増幅率hFEは異なります。
- 通常のダーリントントランジスタ
- インバーテッド・ダーリントントランジスタ
\begin{eqnarray}
h_{FE}=h_{FE1}+h_{FE2}+h_{FE1}{\cdot}h_{FE2}
\end{eqnarray}
\begin{eqnarray}
h_{FE}=h_{FE1}+h_{FE1}{\cdot}h_{FE2}
\end{eqnarray}
まとめ
この記事では『インバーテッド・ダーリントントランジスタ』について、以下の内容を説明しました。
当記事のまとめ
- インバーテッド・ダーリントントランジスタとは
- インバーテッド・ダーリントントランジスタの接続
- インバーテッド・ダーリントントランジスタの特徴
- 電流増幅率hFEの導出方法
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。







