『表面抵抗値』と『表面抵抗率』の違い！単位や測定方法について！

この記事では表面抵抗値と表面抵抗率の違いと各測定方法について詳しく説明します。

『表面抵抗値』と『表面抵抗率』の違い

表面抵抗値

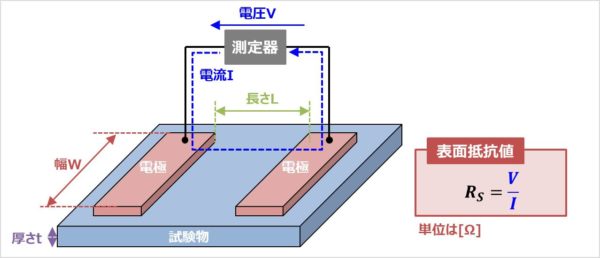
表面抵抗値R_Sとは、その名の通り、試験物の表面の抵抗値です。

表面抵抗値R_Sは、2つの電極間の表面に印加する電圧をV、その時に流れた電流をIとした時、次式で表されます。
\begin{eqnarray}
R_{S}=\frac{V}{I}
\end{eqnarray}

また、表面抵抗値R_Sの単位は[Ω]です。

補足

表面抵抗値は表面抵抗、2点間表面抵抗値、2点間抵抗、点間抵抗など様々な呼ばれ方をしています。
表面抵抗値は英語では「Surface Resistance」と書きます。

表面抵抗率

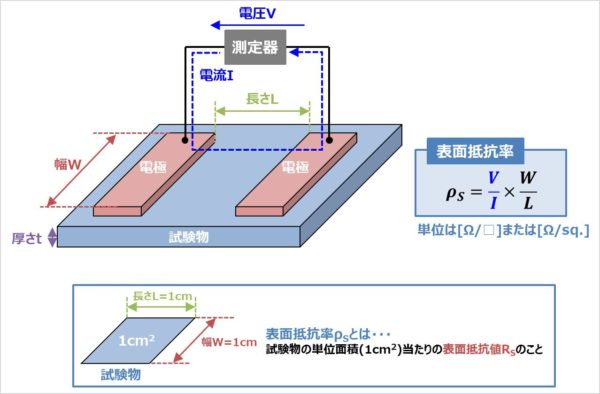
表面抵抗率ρ_Sとは、試験物の単位面積(1cm²)当たりの表面抵抗値です。表面抵抗値R_Sと表面抵抗率ρ_Sは違うので注意しましょう。

表面抵抗率ρ_Sは、2つの電極間の表面に印加する電圧をV、その時に流れた電流をI、電極の幅をW、2つの電極間の距離をLとした時、次式で表されます(後ほど導出方法について説明します)。

\begin{eqnarray}
{\rho}_{S}=\frac{V}{I}×\frac{W}{L}
\end{eqnarray}

表面抵抗率ρ_Sの単位は[Ω/sq.]または[Ω/□]です。読み方は「オーム・パー・スクエア」です。

ガラスやフィルム等の均一で薄い膜、シート状製品の導電性評価や検査では表面抵抗率ρ_Sの測定が一般的に行われます。

補足

表面抵抗率はシート抵抗(sheet Resistance, Sheet Resistivity)や面抵抗率とも呼ばれています。
表面抵抗率は英語では「Surface Resistivity」と書きます。
表面抵抗率の記号は、表面抵抗値R_Sと区別するために、ρ_Sで表すのが一般的です(R_Sで表している場合もあります)。
表面は英語で『Surface』、シートは英語で『Sheet』と書きます。英語に”S”がついていることから、抵抗率ρの下文字に”S“が付きρ_Sとなります。
表面抵抗率は『JIS K 6911』に正式に採用されている用語です。

表面抵抗率の式の導出方法

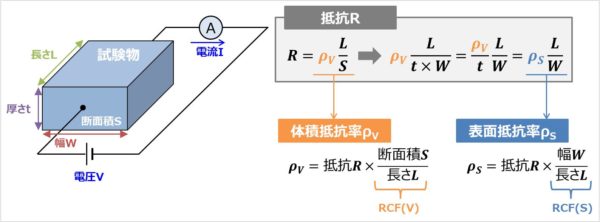
物体の抵抗Rは長さLに比例し、断面積Sに反比例するため、次式で表されます。
\begin{eqnarray}
R={\rho}_{V}×\frac{L}{S}\tag{1}
\end{eqnarray}

上式において、ρ_Vは体積抵抗率といいます。断面積Sを厚さtと幅Wに分解すると、次式となります。
\begin{eqnarray}
R={\rho}_{V}×\frac{L}{t×W}\tag{2}
\end{eqnarray}

体積抵抗率ρ_Vを厚さtで割ったものが表面抵抗率ρ_Sであり、次式で表されます。
\begin{eqnarray}
{\rho}_{S}=\frac{{\rho}_{V}}{t}\tag{3}
\end{eqnarray}

上式を(2)式に代入すると、次式となります。
\begin{eqnarray}
R={\rho}_{S}×\frac{L}{W}\tag{4}
\end{eqnarray}

上式を変形すると、次式となります。
\begin{eqnarray}
{\rho}_{S}=R×\frac{W}{L}=R×RCF(S)\tag{5}
\end{eqnarray}

ここで、RCF(S)は表面抵抗率補正係数(Resistivity Correction Factor)といわれるものであり、「材料の形状や寸法及び測定位置による影響」を補正するために用いられる係数です。

また、抵抗Rは印加する電圧をV、その時に流れた電流をIとした時、次式で表されます。
\begin{eqnarray}
R=\frac{V}{I}\tag{6}
\end{eqnarray}

したがって、(6)式を(5)式に代入すると、表面抵抗率ρ_Sは次式となります。
\begin{eqnarray}
{\rho}_{S}=\frac{V}{I}×\frac{W}{L}=\frac{V}{I}×RCF(S)\tag{7}
\end{eqnarray}

補足

体積抵抗率ρ_Vは物質固有の値ですが、表面抵抗率ρ_Sは厚さtによって変わるのが特徴です。そのため、表面抵抗率ρ_Sは厚みの指標となり、塗膜、薄膜等の分野でよく使われています。なお、厚さtは分母にあるため、物質が厚いほど表面抵抗率ρ_Sが低下します。
幅Wの単位は[cm]、長さLの単位は[cm]、抵抗Rの単位は[Ω]なので、(5)式から表面抵抗率ρ_Sの単位は[Ω]となります。しかし、通常の抵抗の単位の[Ω]と区別するために、表面抵抗率ρ_Sの単位は[Ω/□]または[Ω/sq.]で表すのが一般的です。

『表面抵抗値』と『表面抵抗率』の測定方法

『表面抵抗値』の測定方法

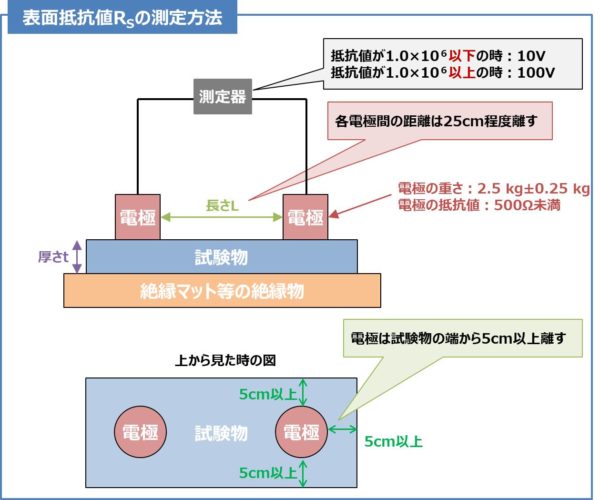
表面抵抗値の測定方法には、『RCJS-5-1』という規格に定められており、以下のようになっています。

表面抵抗値の測定方法

電極は計測する試験物は端から5cm以上離す。
各電極間の距離は25cm程度離す。

→使用する表面抵抗計によって「30cm以上離してください」と書いてある仕様書もあれば、「25cm以上離してください」と書いてある仕様書があります。そのため、使用する表面抵抗計によって距離を変える必要があります。

表面抵抗値が10⁶Ω以下の時は10V、表面抵抗値が10⁶Ωを超えると100Vを印可する。

→表面抵抗値によって、電圧を自動で調整してくれるものもあれば手動で調整しなければならないものもあります。

また、表面抵抗値の測定に使用する電極は『IEC61340-4-1』、『JIS-C2170』、『RCJS-5-1』という規格に定められており、以下のようになっています。

表面抵抗値の測定に使用する電極

電極の重さ

各測定電極の総質量は2.5kg±0.25kgであること

電極の抵抗値

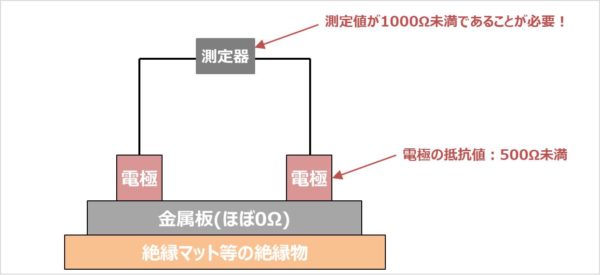
「2つの電極間の点間抵抗が10³Ωより低くなるように十分な導電性をもたなければならない」と規定されています。そのため、各電極の抵抗値は500Ω未満であることが必要です。そのため、下図のような状態で表面抵抗計に表示される値が10³Ω未満であることを確認する必要があります。

『表面抵抗率』の測定方法

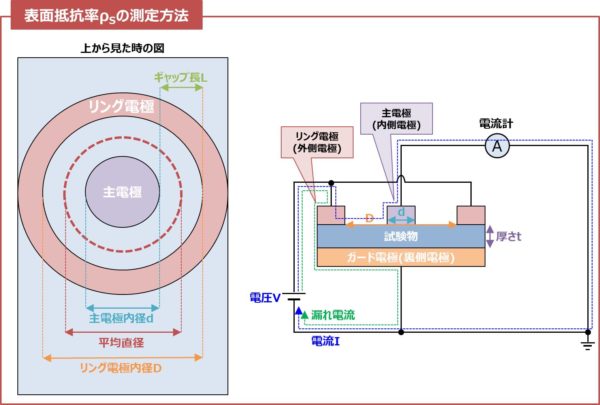
上図のような電極を使用します。

試験物の表面にリング電極(外側電極)と主電極(内側電極)を押し当て、試験物の表面を流れる電流を測定します。

試験物の下に裏側電極を置くことで、試験物の表面を流れる電流のみを測定することができます。表面抵抗率ρ_Sの測定に使用していない裏側電極はガード電極と呼ばれます。

直流電圧Vをリング電極に印可し、リング電極から主電極に向かって試験物表面上に流れる電流Iを測定すると、表面抵抗値R_Sは、
\begin{eqnarray}
R_{S}=\frac{V}{I}
\end{eqnarray}

となります。なお、リング電極からガード電極に漏れ電流が流れますが、試験物表面上に流れる電流の方が多いため表面抵抗値R_Sの計算に使用する電流Iの値には影響を与えません。

したがって、表面抵抗率ρ_Sは、
\begin{eqnarray}
{\rho}_{S}=\frac{V}{I}×\frac{W}{L}=R_{S}×\frac{W}{L}
\end{eqnarray}
となります。ここから幅Wと長さLを求めていきます。

幅Wと長さLの求め方

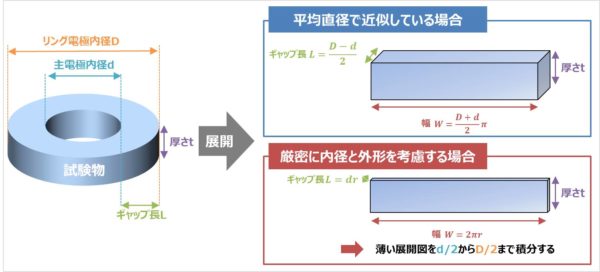
電流が流れるのは、リング電極と主電極の間のドーナツ型の部分です。

このドーナツ型を展開すると、直方体となります。この直方体を平均直径で近似する場合と厳密に内径と外形を考慮する場合で表面抵抗率ρ_Sの式が異なります。

平均直径で近似する場合

この場合は、直方体の幅W(有効周囲長)と長さLは次式となります。
\begin{eqnarray}
W&=&\frac{{\pi}(D+d)}{2}\\
L&=&\frac{D-d}{2}
\end{eqnarray}

したがって、表面抵抗率ρ_Sは、次式となります。
\begin{eqnarray}
{\rho}_{S}&=&R_{S}×\frac{W}{L}\\
&=&R_{S}×\frac{\displaystyle\frac{{\pi}(D+d)}{2}}{\displaystyle\frac{D-d}{2}}\\
&=&R_{S}×\frac{{\pi}(D+d)}{ D-d }
\end{eqnarray}

上式において、dは主電極の内径[cm]、Dはリング電極の内径[cm]です。

なお、『JIS K 6911』の場合、主電極の内径d=50[mm]、リング電極(外側電極)の内径D=70[mm]となるため、表面抵抗率ρ_Sと表面抵抗値R_Sの関係は次式となります。
\begin{eqnarray}
{\rho}_S=18.850×R_{S}
\end{eqnarray}

厳密に内径と外形を考慮する場合

半径rにおける円周上の抵抗R(r)は、幅Wを2πr、高さをt、長さLをdrの薄い展開図だと考えると、
\begin{eqnarray}
R(r)={\rho}_{V}×\frac{L}{t×W}＝{\rho}_{V}×\frac{dr}{t×2{\pi}r}
\end{eqnarray}

となります。ここで、体積抵抗率ρ_Vを厚さtで割ったものを表面抵抗率ρ_Sなので、
\begin{eqnarray}
R(r)={\rho}_{S}×\frac{dr}{2{\pi}r}
\end{eqnarray}

となります。このrを主電極の半径d/2からリング電極の半径D/2まで積分することで、リング電極と主電極の間のドーナツ型の部分の表面抵抗値R_Sを求めることができます。
\begin{eqnarray}
R_{S}=\displaystyle\int_{d/2}^{D/2}R(r)=\displaystyle\int_{d/2}^{D/2}{\rho}_{S}×\frac{1}{2{\pi}r}dr=\frac{{\rho}_{S}}{2{\pi}}×{\ln}\frac{D}{d}
\end{eqnarray}

したがって、表面抵抗率ρ_Sは、次式となります。
\begin{eqnarray}
{\rho}_{S}=\frac{2{\pi}}{{\ln}\displaystyle\frac{D}{d}}×R_{S}
\end{eqnarray}

なお、『JIS K 6911』の場合、主電極の内径d=50[mm]、リング電極(外側電極)の内径D=70[mm]となるため、表面抵抗率ρ_Sと表面抵抗値R_Sの関係は次式となります。
\begin{eqnarray}
{\rho}_S=18.674×R_{S}
\end{eqnarray}

平均直径で近似する場合とほどんど同じになりましたね。