この記事では『方形波』について
- 実効値・平均値・波形率・波高率の求め方
などを図を用いて分かりやすく説明しています。
方形波の実効値・平均値・波形率・波高率
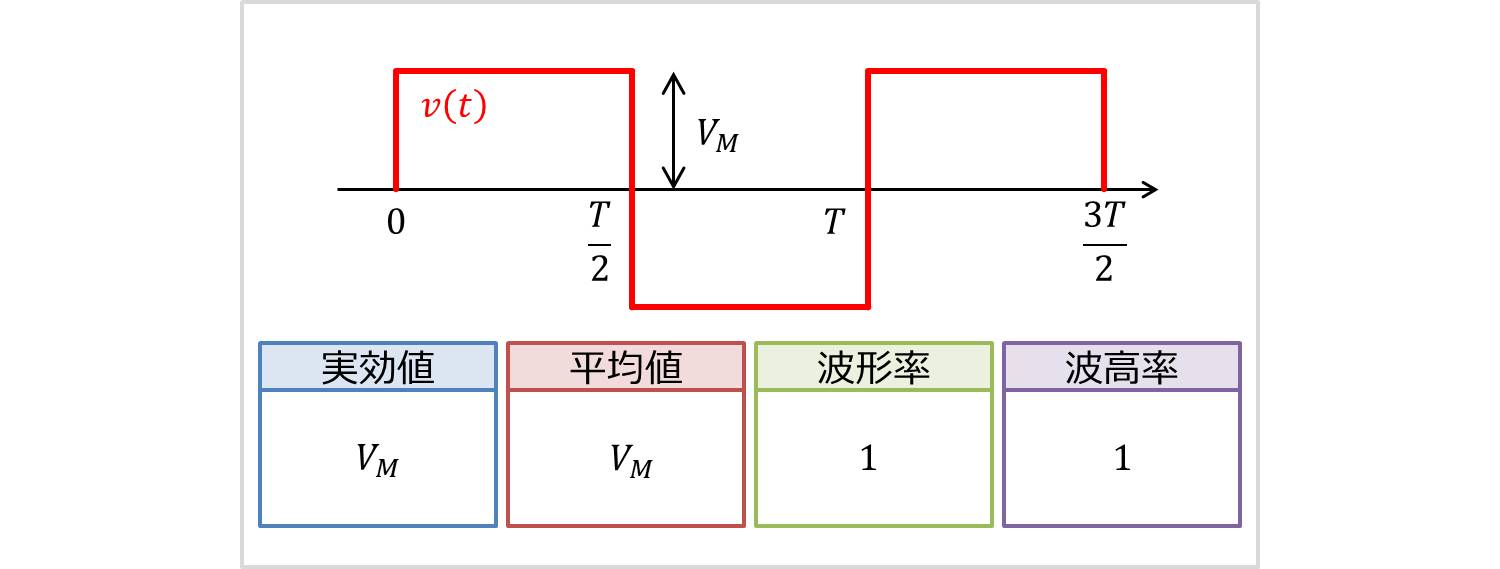
最初に方形波(最大値\(V_M\)、周期\(T\))の実効値・平均値・波形率・波高率を上図に示します。
これから各値がどのように求まるのかを説明します(できるだけ途中式を多くするよう心がけています)。
方形波は三角波や台形波の計算と比較するとかなり楽です。
方形波の波形式
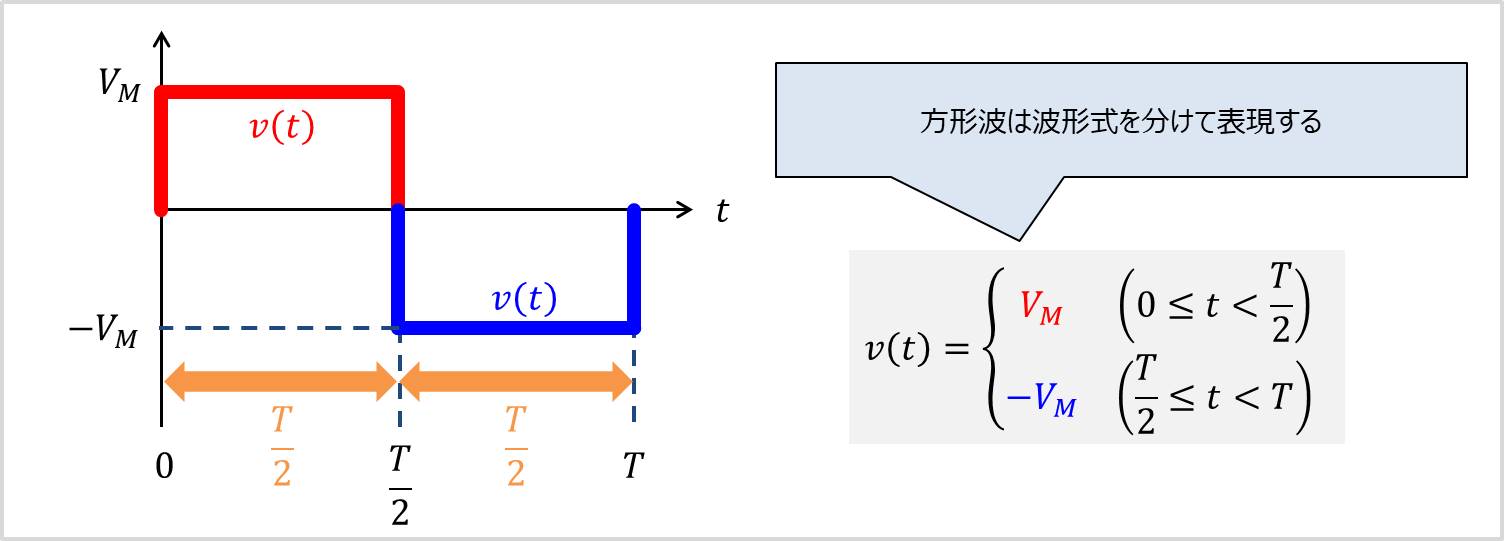
方形波の実効値・平均値を求めるためには、最初に方形波を式で表す必要があります。
方形波は2つの直線で表すことができます。
上図では方形波を赤色の直線と青色の直線で分けています。
赤色の直線の領域は「\(0 \leq t \lt \displaystyle \frac{T}{2}\)」、青色の直線の領域は「\(\displaystyle \frac{T}{2} \leq t \lt T\)」となっています。
各直線の式を求めます。
赤色の直線
「\(0 \leq t \lt \displaystyle \frac{T}{2}\)」の領域が赤色の直線です。
赤色の直線は、時間\(\displaystyle \frac{T}{2}\)の間、常に\(V_M\)となっています。
そのため、赤色の直線の式は
v(t)=V_M
\end{eqnarray}
で表すことができます。
青色の直線
「\(\displaystyle \frac{T}{2} \leq t \lt T\)」の領域が青色の直線です。
青色の直線は、時間\(\displaystyle \frac{T}{2}\)の間、常に\(-V_M\)となっています。
そのため、青色の直線の式は
v(t)=-V_M
\end{eqnarray}
で表すことができます。
赤色の直線と青色の直線を合わせると、
v(t) = \begin{cases}
V_M & \left(0 \leq t \lt \displaystyle \frac{T}{2}\right) \\
-V_M & \left(\displaystyle \frac{T}{2} \leq t \lt T\right)
\end{cases}
\end{eqnarray}
となります。これ方形波の波形式です。
方形波の実効値
波形\(v(t)\)の実効値\(V_{RMS}\)は、\(v(t)\)を2乗して平均した値の平方根なので、
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}v(t)^2dt}
\end{eqnarray}
と表されます。
赤色の直線の領域は「\(0 \leq t \lt \displaystyle \frac{T}{2}\)」、青色の直線の領域は「\(\displaystyle \frac{T}{2} \leq t \lt T\)」です。
絶対値を求める式において、赤色の直線と青色の直線を分けると、
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T/2}v(t)^2dt+\displaystyle \int_{T/2}^{T}v(t)^2dt\right )}
\end{eqnarray}
となります。
上式を解くと、
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T/2}v(t)^2dt+\displaystyle \int_{T/2}^{T}v(t)^2dt\right )}\\
&=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T/2}{V_M}^2dt+\displaystyle \int_{T/2}^{T}(-V_M)^2dt\right )}\\
&=& \sqrt{\displaystyle\frac{1}{T}\displaystyle \int_{0}^{T}{V_M}^2dt}\\
&=& \sqrt{\displaystyle\frac{1}{T}\left[{V_M}^2t\right]_{0}^{T}}\\
&=& \sqrt{\displaystyle\frac{1}{T}{V_M}^2T}\\
&=& V_M
\end{eqnarray}
以上より、方形波の実効値\(V_{RMS}\)は、
V_{RMS} &=& V_M
\end{eqnarray}
となります。
方形波の平均値
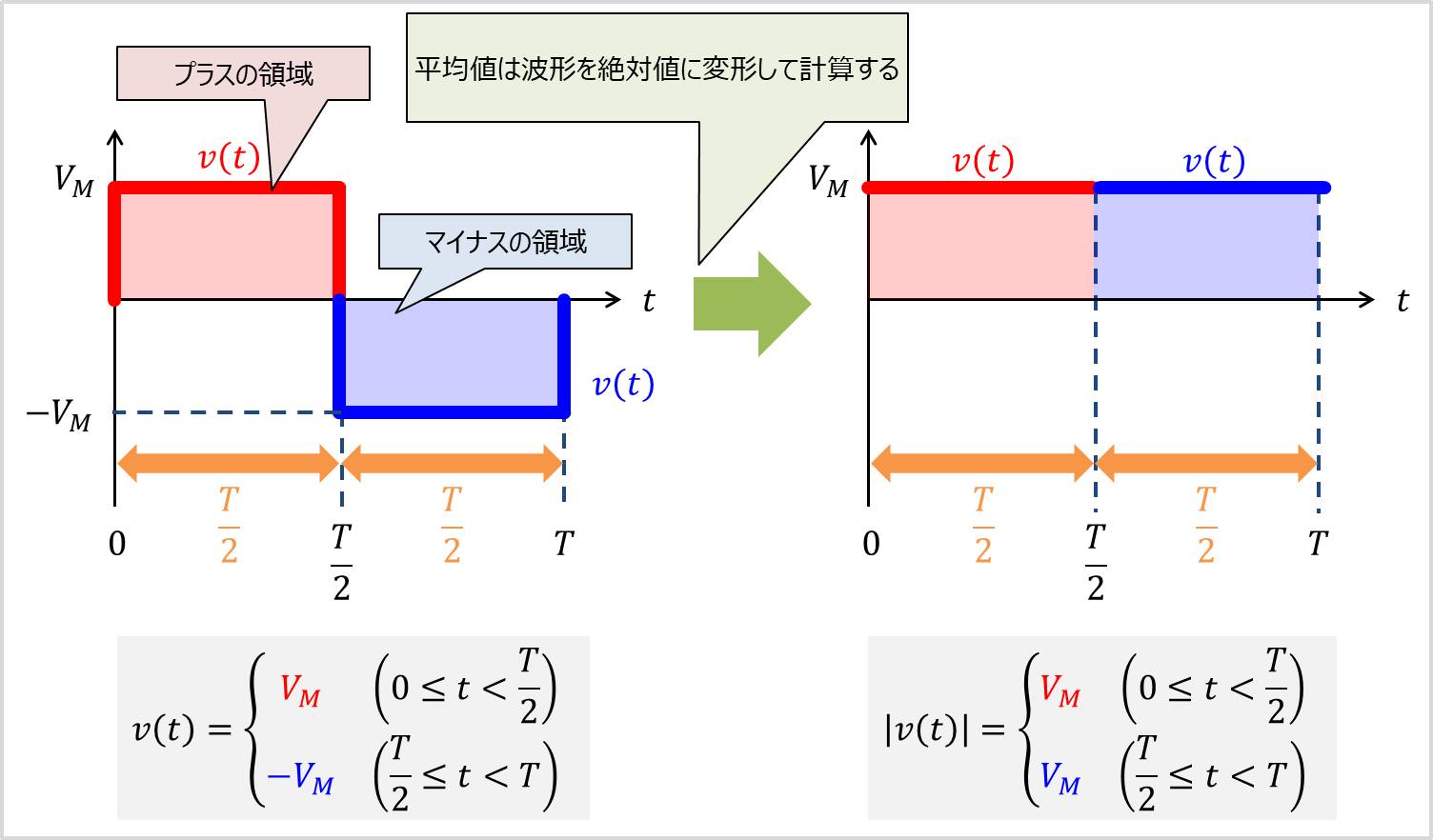
波形\(v(t)\)の平均値\(V_{AVE}\)は\(v(t)\)の絶対値\(|v(t)|\)を平均した値なので、
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}|v(t)|dt
\end{eqnarray}
と表されます。
平均値を求める式は\(v(t)\)の絶対値\(|v(t)|\)を使用します。
そのため、波形のマイナスの領域(薄い青の箇所)はプラス(薄い赤の箇所)になるように変換する必要があります。
領域\(\left(0 \leq t \lt \displaystyle \frac{T}{2}\right)\)は波形\(v(t)\)がプラスなので、何も変換しません。
領域\(\left(\displaystyle \frac{T}{2} \leq t \lt T\right)\)は波形\(v(t)\)がマイナスなので、プラスになるように式にマイナスをかけます。
したがって、\(v(t)\)の絶対値\(|v(t)|\)の式は
|v(t)| = \begin{cases}
V_M & \left(0 \leq t \lt \displaystyle \frac{T}{2}\right) \\
V_M & \left(\displaystyle \frac{T}{2} \leq t \lt T\right)
\end{cases}
\end{eqnarray}
となります。
すなわち、方形波\(v(t)\)の絶対値\(|v(t)|\)の式は
\begin{eqnarray}
|v(t)| = V_M
\end{eqnarray}
になります。
平均値を求める式において、\(|v(t)| = V_M\)を代入すると
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}|v(t)|dt\\
&=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}V_M dt\\
&=& \displaystyle\frac{1}{T} \left[{V_M}t\right]_{0}^{T}\\
&=& V_M
\end{eqnarray}
となります。
以上より、方形波\(v(t)\)の平均値\(V_{AVE}\)は、
V_{AVE} &=& V_M
\end{eqnarray}
となります。
方形波の波形率
波形率は以下の式で表すことができます。
波形率 &=& \displaystyle\frac{実効値V_{RMS}}{平均値V_{AVE}}
\end{eqnarray}
方形波の実効値\(V_{RMS}\)と平均値\(V_{AVE}\)は求まっているので、この式に代入することで方形波の波形率を求めることができます。
波形率 = \displaystyle\frac{V_M}{V_M} = 1
\end{eqnarray}
方形波の最大値
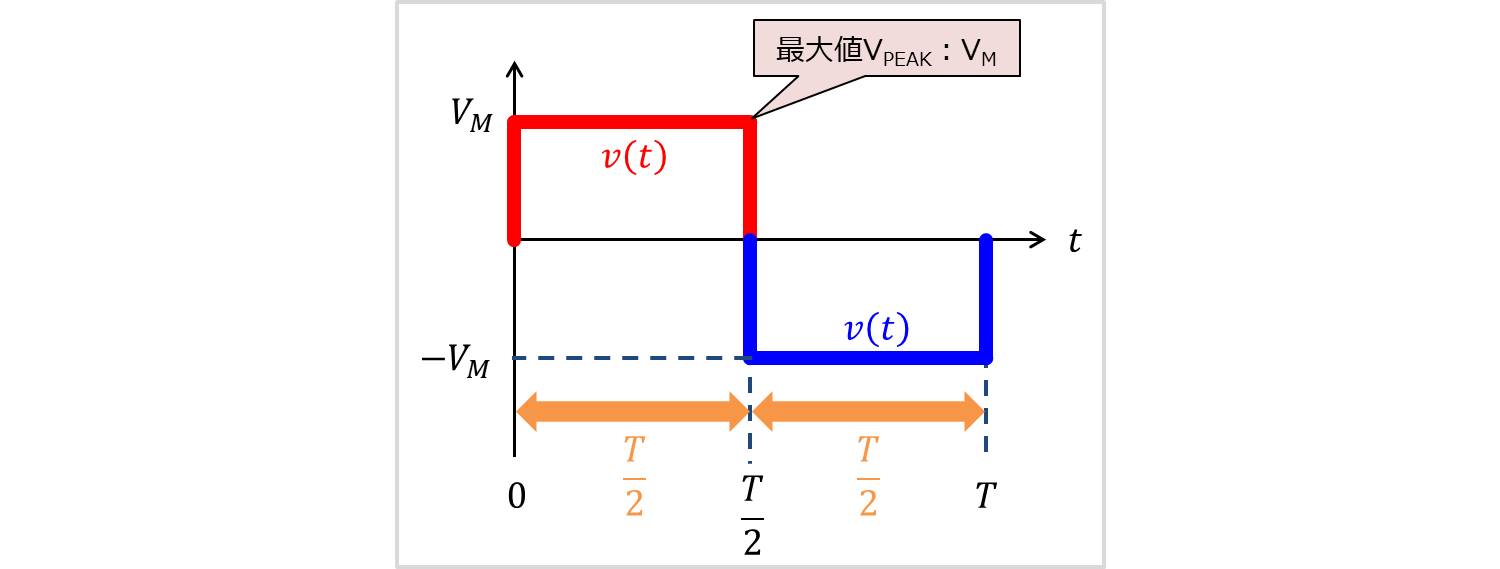
方形波の最大値\(V_{PEAK}\)は波形から分かるように、
最大値V_{PEAK}=V_M
\end{eqnarray}
となります。
方形波の波高率(クレストファクタ)
波高率(クレストファクタ)は以下の式で表すことができます。
波高率 &=& \displaystyle\frac{最大値V_{PEAK}}{実効値V_{RMS}}
\end{eqnarray}
方形波の実効値\(V_{RMS}\)と最大値\(V_{PEAK}\)は求まっているので、この式に代入することで方形波の波高率(クレストファクタ)を求めることができます。
波高率 = \displaystyle\frac{V_M}{V_M} = 1
\end{eqnarray}
まとめ
上のように方形波の実効値・平均値・波形率・波高率を求めました。
方形波の波形式がシンプルなので、各項目を求める計算がかなり楽です。






