この記事では『RLC並列共振回路』について
- RLC並列共振回路とは
- RLC並列共振回路の「インピーダンス」と「共振周波数」
- RLC並列共振回路の「周波数特性」と「Q値」
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
RLC並列共振回路とは
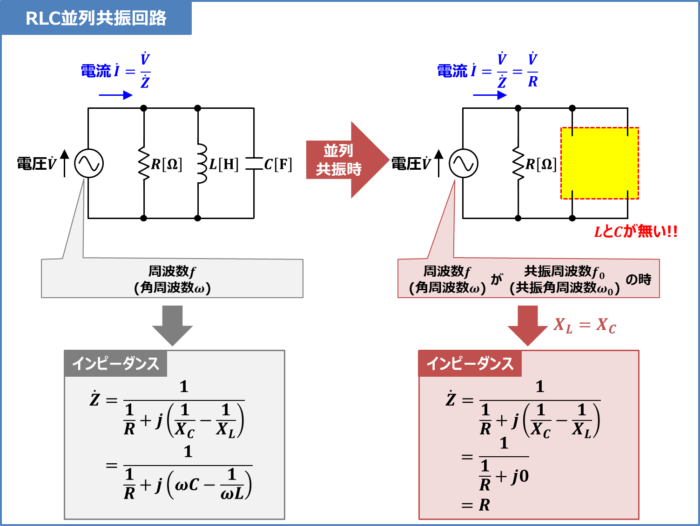
RLC並列共振回路は、抵抗\(R\)とインダクタ\(L\)とコンデンサ\(C\)を並列接続した回路です。
インダクタ\(L\)とコンデンサ\(C\)が並列接続されている回路は「ある周波数」で並列共振するため、RLC並列"共振"回路と呼ばれています。この「ある周波数」は共振周波数といいます。共振周波数の記号は\(f_0\)または\(f_R\)で表されていることが多いです(この記事では\(f_0\)で表しています)。
では、RLC並列共振回路において、共振周波数\(f_0\)で並列共振している時はどのような状態なのでしょうか?
最初に結論から言うと、RLC並列共振回路が共振周波数\(f_0\)で並列共振している時、インダクタ\(L\)のリアクタンス\(X_L={\omega}L\)とコンデンサ\(C\)のリアクタンス\(X_C=\displaystyle\frac{1}{{\omega}C}\)が打ち消し合っています(\(X_L=X_C\)になっているということ)。
また、共振周波数\(f_0\)の時、RLC並列共振回路のインピーダンスは\({\dot{Z}}=R\)、RLC並列共振回路に流れる電流は\({\dot{I}}=\displaystyle\frac{V}{R}\)となり、式からインダクタ\(L\)とコンデンサ\(C\)が無くなります。すなわち、見かけ上、インダクタ\(L\)とコンデンサ\(C\)が無くなり、抵抗\(R\)のみが接続されている回路になります。
では、次に、上記の状態をRLC並列共振回路のインピーダンスの式から考えてみましょう。
RLC並列共振回路の「インピーダンス」と「共振周波数」
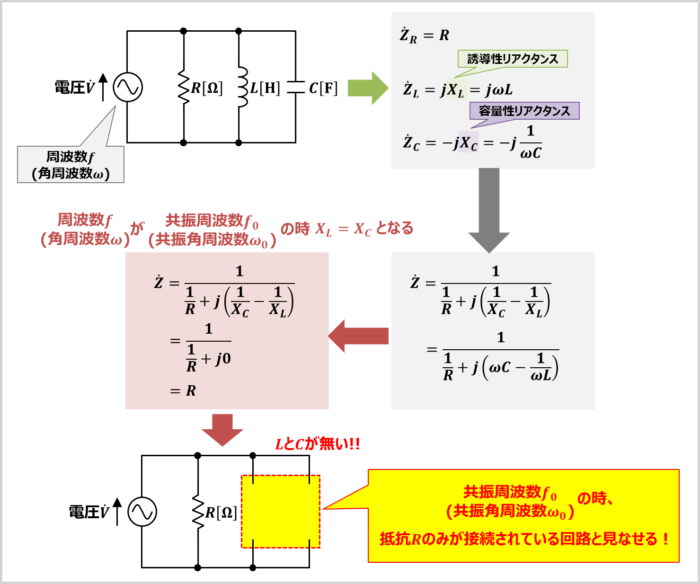
RLC並列共振回路は上図に示すように、抵抗\(R\)とインダクタ\(L\)とコンデンサ\(C\)を並列接続した回路です。
抵抗\(R\)の抵抗値を\(R{\mathrm{[{\Omega}]}}\)、インダクタ\(L\)のインダクタンスを\(L{\mathrm{[H]}}\)、コンデンサ\(C\)の静電容量を\(C{\mathrm{[F]}}\)とすると、抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)、インダクタ\(L\)のインピーダンス\({\dot{Z}}_L\)、コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)は次式で表されます。
\begin{eqnarray}
{\dot{Z}}_R&=&R\tag{1}\\
\\
{\dot{Z}}_L&=&jX_L=j{\omega}L\tag{2}\\
\\
{\dot{Z}}_C&=&-jX_C=-j\frac{1}{{\omega}C}=\frac{1}{j{\omega}C}\tag{3}
\end{eqnarray}
(2)式と(3)式において、\(X_L\)は誘導性リアクタンス(インダクタ\(L\)の抵抗成分)、\(X_C\)は容量性リアクタンス(コンデンサの抵抗成分)と呼ばれています。また、\({\omega}\)は角周波数(角速度とも呼ばれる)であり、\({\omega}=2{\pi}f\)の関係があります。
あわせて読みたい
『リアクタンス』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る
【リアクタンスとは】『単位』や『計算方法』などのまとめ!
『それぞれのインピーダンスの逆数の和』が『RLC並列回路のインピーダンス\({\dot{Z}}\)の逆数』となるため、次式が成り立ちます。
\begin{eqnarray}
\frac{1}{{\dot{Z}}}&=&\frac{1}{{\dot{Z}_R}}+\frac{1}{{\dot{Z}_L}}+\frac{1}{{\dot{Z}_C}}\\
\\
&=&\frac{1}{R}+\frac{1}{jX_L}+\frac{1}{-jX_C}\\
\\
&=&\frac{1}{R}+j\left(\frac{1}{X_C}-\frac{1}{X_L}\right)\\
\\
&=&\frac{1}{R}+j\left(\frac{1}{\displaystyle\frac{1}{{\omega}C}}-j\frac{1}{{\omega}L}\right)\\
\\
&=&\frac{1}{R}+j\left({\omega}C-\frac{1}{{\omega}L}\right)\tag{4}
\end{eqnarray}
上式の分母と分子をひっくり返すと次式となります。
\begin{eqnarray}
{\dot{Z}}=\frac{1}{\displaystyle\frac{1}{R}+j\left(\displaystyle\frac{1}{X_C}-\displaystyle\frac{1}{X_L}\right)}=\frac{1}{\displaystyle\frac{1}{R}+j\left({\omega}C-\displaystyle\frac{1}{{\omega}L}\right)}\tag{5}
\end{eqnarray}
また、RLC並列共振回路の合成インピーダンスの大きさ\(Z\)は次式となります。
\begin{eqnarray}
Z=|{\dot{Z}}|&=&\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left(\displaystyle\frac{1}{X_C}-\displaystyle\frac{1}{X_L}\right)^2}}\\
\\
&=&\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left({\omega}C-\displaystyle\frac{1}{{\omega}L}\right)^2}}\tag{6}
\end{eqnarray}
あわせて読みたい
『RLC並列共振回路の合成インピーダンス』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る


RLC並列回路の『合成インピーダンス』を分かりやすく解説!
RLC並列共振回路は、インダクタ\(L\)のリアクタンス\(X_L={\omega}L\)とコンデンサ\(C\)のリアクタンス\(X_C=\displaystyle\frac{1}{{\omega}C}\)が打ち消し合っている時(\(X_L=X_C\)の時)、並列共振しています。この時の角周波数\({\omega}\)を共振角周波数\({\omega}_0\)とすると、次式が成り立ちます。
\begin{eqnarray}
X_L&=&X_C\\
\\
{\Leftrightarrow}{{\omega}_0}L&=&\frac{1}{{{\omega}_0}C}\tag{7}\\
\\
{\Leftrightarrow}{{\omega}_0}C-\frac{1}{{{\omega}_0}L}&=&0\tag{8}
\end{eqnarray}
(7)式を用いると、RLC並列共振回路の共振角周波数\({\omega}_0\)と共振周波数\(f_0\)を求めることができ、次式となります。
\begin{eqnarray}
{{\omega}_0}L&=&\frac{1}{{{\omega}_0}C}\\
\\
{\Leftrightarrow}{{\omega}_0}^2LC&=&1\\
\\
{\Leftrightarrow}{\omega}_0&=&\frac{1}{\sqrt{LC}}\tag{9}\\
\\
{\Leftrightarrow}f_0&=&\frac{1}{2{\pi}\sqrt{LC}}\tag{10}
\end{eqnarray}
(9)式と(10)式から、RLC並列共振回路の共振角周波数\({\omega}_0\)と共振周波数\(f_0\)はインダクタ\(L\)とコンデンサ\(C\)によって決まり、抵抗の抵抗値\(R\)は無関係ということが分かります。
また、(8)式を用いると、共振周波数\(f_0\)(共振角周波数\({\omega}_0\))の時、RLC並列共振回路のインピーダンス\({\dot{Z}}\)とその大きさ\(Z\)は次式となります。
\begin{eqnarray}
{\dot{Z}}&=&\frac{1}{\displaystyle\frac{1}{R}+j\left({\omega}_0C-\displaystyle\frac{1}{{\omega}_0L}\right)}=\frac{1}{\displaystyle\frac{1}{R}+j0}=\frac{1}{\displaystyle\frac{1}{R}}=R\tag{11}\\
\\
Z&=&\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left({\omega}_0C-\displaystyle\frac{1}{{\omega}_0L}\right)^2}}=\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+0^2}}=\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2}}=R\tag{12}
\end{eqnarray}
(11)式と(12)式を見てみましょう。共振周波数\(f_0\)(共振角周波数\({\omega}_0\))の時、RLC並列共振回路のインピーダンスの式からインダクタ\(L\)とコンデンサ\(C\)が無くなっています。すなわち、共振周波数\(f_0\)(共振角周波数\({\omega}_0\))の時、RLC並列共振回路はインダクタ\(L\)とコンデンサ\(C\)が無くなり、抵抗\(R\)のみが接続されている回路と見なすことができます。
補足
- RLC並列共振回路の場合には、共振周波数のことを「並列共振周波数」と呼ぶこともあります。逆に、RLC直列共振回路の場合には、共振周波数のことを「直列共振周波数」と呼ぶこともあります。
RLC並列共振回路の「周波数特性」と「Q値」
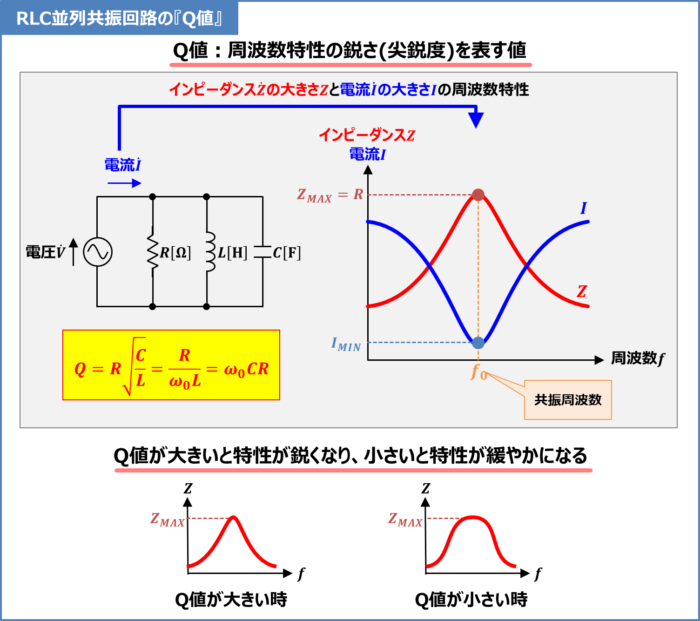

(5)式で表しているRLC並列共振回路のインピーダンスの大きさ\(Z\)の周波数特性は上図のようになります。
周波数特性から分かるように、RLC並列共振回路のインピーダンスの大きさ\(Z\)は、共振周波数\(f_0\)の時に最大値\(Z_{MAX}=R\)となり、共振周波数\(f_0\)から離れるほど、小さくなります。そのため、共振周波数\(f_0\)の時、RLC並列共振回路に流れる電流の大きさ\(I\)が最小値\(I_{MIN}\)となり、\(I_{MIN}\)は次式で表されます。
\begin{eqnarray}
I_{MIN}&=&\frac{V}{Z_{MAX}}\\
\\
&=&\frac{V}{R}\tag{13}
\end{eqnarray}
また、共振回路にはQ値と呼ばれる値があります。Q値は周波数特性の鋭さを表す値であり、Q値が大きいほど特性が鋭くなり、小さいほど特性が緩やかになります。
RLC並列共振回路の場合、Q値は次式で表されます。
\begin{eqnarray}
Q=R\sqrt{\frac{C}{L}}=\frac{R}{{\omega}_0L}={\omega}_0CR\tag{14}
\end{eqnarray}
抵抗\(R\)の抵抗値が大きいほど、インダクタ\(L\)のインダクタンスが小さいほど、コンデンサ\(C\)の静電容量が大きいほど、Q値が大きくなるので、周波数特性が鋭くなります。
あわせて読みたい
『RLC並列共振回路のQ値』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る


RLC並列共振回路の『Q値』とは?導出方法などを解説!
まとめ
この記事では『RLC並列共振回路』について、以下の内容を説明しました。
- RLC並列共振回路とは
- RLC並列共振回路の「インピーダンス」と「共振周波数」
- RLC並列共振回路の「周波数特性」と「Q値」
お読み頂きありがとうございました。
本記事のポイント
- RLC並列共振回路の共振角周波数\({\omega}_0\)と共振周波数\(f_0\)は次式で表される。
\begin{eqnarray}
{\omega}_0&=&\frac{1}{\sqrt{LC}}\\
\\
f_0&=&\frac{1}{2{\pi}\sqrt{LC}}
\end{eqnarray}
- 共振周波数\(f_0\)(共振角周波数\({\omega}_0\))の時、インピーダンスの大きさ\(Z\)が最大値\(Z_{MAX}=R\)となるので、RLC並列共振回路に流れる電流の大きさ\(I\)が最小値\(I_{MIN}=\displaystyle\frac{V}{R}\)となる。
- RLC並列共振回路のインピーダンスの大きさ\(Z\)の周波数特性の鋭さはQ値によって決まる。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






