この記事では『RLC並列共振回路』について
- RLC並列共振回路のQ値とは
- RLC並列共振回路のQ値の「導出方法」
- 「Q値」と「インダクタ\(L\)とコンデンサ\(C\)に流れる電流」の関係
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
RLC並列共振回路のQ値とは
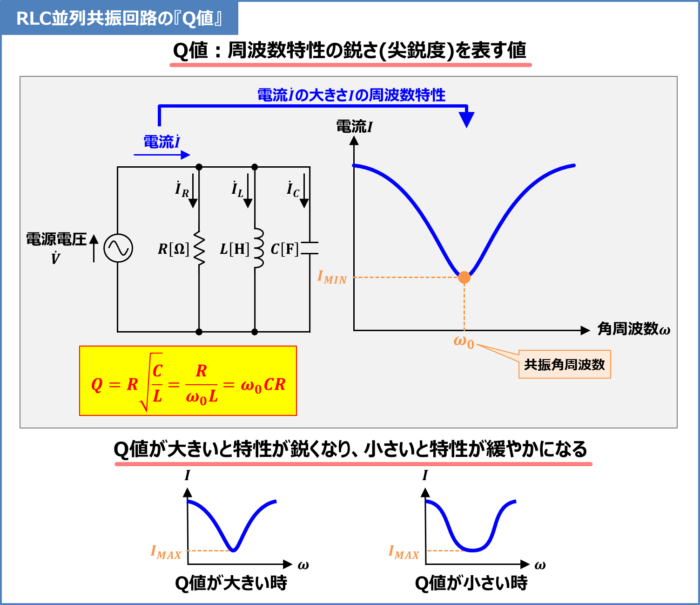
Q値とは周波数特性の鋭さ(尖鋭度)を表す値です。Q値が大きいと特性が鋭くなり、小さいと特性が緩やかになります。
上図にRLC並列共振回路に流れる電流の大きさ\(I\)の周波数特性を示しています。RLC並列共振回路は、抵抗\(R\)とインダクタ\(L\)とコンデンサ\(C\)を並列接続した回路であり、インダクタ\(L\)とコンデンサ\(C\)が共振する角周波数\({\omega}_0\left(=\displaystyle\frac{1}{\sqrt{LC}}\right)\)で電流の大きさ\(I\)が最小値\(I_{MIN}\)になります。
このRLC並列共振回路において、Q値は次式で表されます(次式の導出方法については後ほど説明します)。
RLC並列共振回路の『Q値』
\begin{eqnarray}
Q=R\sqrt{\frac{C}{L}}=\frac{R}{{\omega}_0L}={\omega}_0CR\tag{1}
\end{eqnarray}
上式において、\({\omega}_0\)は共振角周波数、\(R\)は抵抗の抵抗値、\(L\)はインダクタの自己インダクタンス、\(C\)はコンデンサの静電容量となります。
補足
- Qは「Quality factor(品質要素)」のQからとった記号です。
- Q値は「共振回路の良さ(共振回路の損失の少なさ)」を表す指標です。RLC並列共振回路の場合、抵抗値\(R\)が大きいほど、Q値が大きくなります。それは、抵抗値\(R\)が大きいほど、抵抗に流れる電流\(I_R\)が小さくなり、抵抗に流れる電流\(I_R\)によって生じる損失が小さくなるからです。
あわせて読みたい
『RLC並列共振回路の特徴等』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る
RLC並列共振回路とは?特徴や共振周波数の導出など!
RLC並列共振回路のQ値の導出
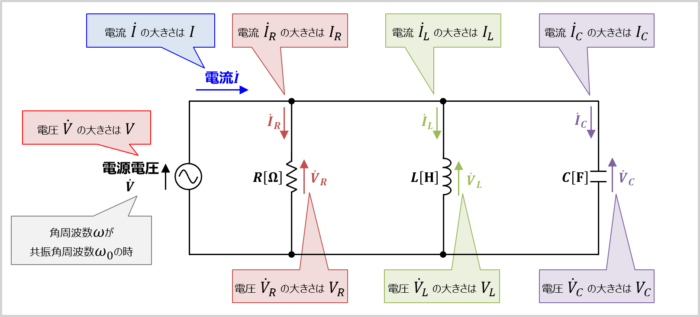

RLC並列共振回路は上図に示すように、抵抗\(R\)とインダクタ\(L\)とコンデンサ\(C\)を並列接続した回路です。抵抗\(R\)の抵抗値を\(R{\mathrm{[{\Omega}]}}\)、インダクタ\(L\)のインダクタンスを\(L{\mathrm{[H]}}\)、コンデンサ\(C\)の静電容量を\(C{\mathrm{[F]}}\)とします。
RLC並列共振回路におけるQ値の定義は「共振時にインダクタ\(L\)に流れる電流の大きさ\(I_L\)(またはコンデンサ\(C\)に流れる電流の大きさ\(I_C\))」と「共振時に抵抗\(R\)に流れる電流の大きさ\(I_R\)」の比となります。この定義を式で書くと、RLC並列共振回路のQ値は次式で表されます。
\begin{eqnarray}
Q=\frac{I_L}{I_R}=\frac{I_C}{I_R}\tag{2}
\end{eqnarray}
ここで、共振角周波数\({\omega}_0\)の時に「抵抗\(R\)に流れる電流の大きさ\(I_R\)」と「インダクタ\(L\)に流れる電流の大きさ\(I_L\)」と「コンデンサ\(C\)に流れる電流の大きさ\(I_C\)」を求めてみましょう。
- 抵抗\(R\)に流れる電流の大きさ\(I_R\)
- 抵抗\(R\)にかかる電圧の大きさ\(V_R\)は電源電圧の大きさ\(V\)となるため、抵抗\(R\)に流れる電流の大きさ\(I_R\)は次式で表されます。
\begin{eqnarray}
I_R=\frac{V_R}{R}=\frac{V}{R}\tag{3}
\end{eqnarray}
- 抵抗\(R\)にかかる電圧の大きさ\(V_R\)は電源電圧の大きさ\(V\)となるため、抵抗\(R\)に流れる電流の大きさ\(I_R\)は次式で表されます。
- インダクタ\(L\)に流れる電流の大きさ\(I_L\)
- インダクタ\(L\)にかかる電圧の大きさ\(V_L\)は電源電圧の大きさ\(V\)となります。また、インダクタ\(L\)のリアクタンスの大きさ\(X_L\)は「\(X_L={\omega}L\)」で表されます。そのため、共振角周波数\({\omega}_0\)の時、インダクタ\(L\)に流れる電流の大きさ\(I_L\)は次式で表されます。
\begin{eqnarray}
I_L=\frac{V_L}{X_L}=\frac{V}{{\omega}_0L}\tag{4}
\end{eqnarray}
- インダクタ\(L\)にかかる電圧の大きさ\(V_L\)は電源電圧の大きさ\(V\)となります。また、インダクタ\(L\)のリアクタンスの大きさ\(X_L\)は「\(X_L={\omega}L\)」で表されます。そのため、共振角周波数\({\omega}_0\)の時、インダクタ\(L\)に流れる電流の大きさ\(I_L\)は次式で表されます。
- コンデンサ\(C\)に流れる電流の大きさ\(I_C\)
- コンデンサ\(C\)にかかる電圧の大きさ\(V_C\)は電源電圧の大きさ\(V\)となります。また、コンデンサ\(C\)のリアクタンスの大きさ\(X_C\)は「\(X_C=\displaystyle\frac{1}{{\omega}C}\)」で表されます。そのため、共振角周波数\({\omega}_0\)の時、コンデンサ\(C\)に流れる電流の大きさ\(I_C\)は次式で表されます。
\begin{eqnarray}
I_C=\frac{V_C}{X_C}=\frac{V}{\displaystyle\frac{1}{{\omega}_0C}}={\omega}_0CV\tag{5}
\end{eqnarray}
- コンデンサ\(C\)にかかる電圧の大きさ\(V_C\)は電源電圧の大きさ\(V\)となります。また、コンデンサ\(C\)のリアクタンスの大きさ\(X_C\)は「\(X_C=\displaystyle\frac{1}{{\omega}C}\)」で表されます。そのため、共振角周波数\({\omega}_0\)の時、コンデンサ\(C\)に流れる電流の大きさ\(I_C\)は次式で表されます。
(2)~(5)式より、RLC並列共振回路のQ値は次式となります。
\begin{eqnarray}
Q&=&\frac{I_L}{I_R}=\frac{\displaystyle\frac{V}{{\omega}_0L}}{\displaystyle\frac{V}{R}}=\frac{R}{{\omega}_0L}\tag{6}\\
\\
Q&=&\frac{I_C}{I_R}=\frac{{\omega}_0CV}{\displaystyle\frac{V}{R}}={\omega}_0CR\tag{7}\\
\end{eqnarray}
また、(6)式または(7)式において、「\({\omega}_0=\displaystyle\frac{1}{\sqrt{LC}}\)」を用いると次式が成り立ちます。
\begin{eqnarray}
Q=R\sqrt{\frac{C}{L}}\tag{8}
\end{eqnarray}
これで、RLC並列共振回路のQ値の導出を終わります。
「Q値」と「インダクタLとコンデンサCに流れる電流」の関係
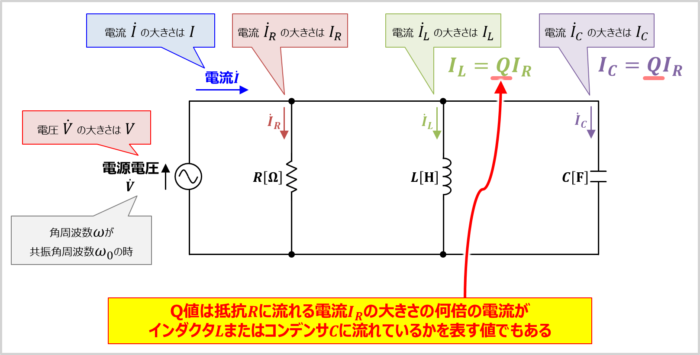

(6)式より、共振角周波数\({\omega}_0\)の時、インダクタ\(L\)に流れる電流の大きさ\(I_L\)は次式となります。
\begin{eqnarray}
I_L=Q×I_R\tag{9}
\end{eqnarray}
同様に、(7)式より、コンデンサ\(C\)に流れる電流の大きさ\(I_C\)は次式となります。
\begin{eqnarray}
I_C=Q×I_R\tag{10}
\end{eqnarray}
したがって、Q値は抵抗\(R\)に流れる電流の大きさ\(I_R\)の何倍の電流がインダクタ\(L\)またはコンデンサ\(C\)に流れているかを表す値でもあります。Q値が大きければ大きいほど、インダクタ\(L\)とコンデンサ\(C\)に流れる電流が大きくなります。
ここで、もう少しRLC並列共振回路について深掘りしてみましょう。冒頭でRLC並列共振回路は「インダクタ\(L\)とコンデンサ\(C\)が共振する角周波数\({\omega}_0\left(=\displaystyle\frac{1}{\sqrt{LC}}\right)\)で電流の大きさ\(I\)が最小値\(I_{MIN}\)になる」と説明しましたが、この\(I_{MIN}\)の値を導出します。
RLC並列共振回路の合成アドミタンス\({\dot{Y}}\)は次式となります。
\begin{eqnarray}
{\dot{Y}}&=&\frac{1}{R}+\frac{1}{j{\omega}L}+j{\omega}C\\
\\
&=&\frac{1}{R}+j\left({\omega}C-\frac{1}{{\omega}L}\right)\tag{11}
\end{eqnarray}
上式において、\({\omega}\)は角周波数(角速度とも呼ばれる)であり、\({\omega}=2{\pi}f\)の関係があります。
また、RLC並列共振回路の合成アドミタンスの大きさ\(Y\)は次式となります。
\begin{eqnarray}
Y=|{\dot{Y}}|=\sqrt{\left(\frac{1}{R}\right)^2+\left({\omega}C-\displaystyle\frac{1}{{\omega}L}\right)^2}\tag{12}
\end{eqnarray}
あわせて読みたい
『RLC並列共振回路の合成アドミタンス』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る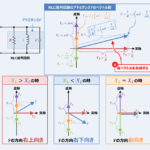


【RLC並列回路のアドミタンス】計算方法やベクトル図を解説!
したがって、RLC並列共振回路に流れる電流の大きさ\(I\)は、電源電圧の大きさを\(V\)とすると次式で表されます。
\begin{eqnarray}
I=VY=V\sqrt{\left(\frac{1}{R}\right)^2+\left({\omega}C-\displaystyle\frac{1}{{\omega}L}\right)^2}\tag{13}
\end{eqnarray}
インダクタ\(L\)とコンデンサ\(C\)が共振する角周波数(共振角周波数)\({\omega}_0\left(=\displaystyle\frac{1}{\sqrt{LC}}\right)\)の時、次式が成り立ちます。
\begin{eqnarray}
{\omega}_0&=&\frac{1}{\sqrt{LC}}\\
\\
{\Leftrightarrow}{{\omega}_0}^2&=&\frac{1}{LC}\\
\\
{\Leftrightarrow}{{\omega}_0}L&=&\frac{1}{{{\omega}_0}C}\\
\\
{\Leftrightarrow}{\omega}_0C-\displaystyle\frac{1}{{\omega}_0L}&=&0\tag{14}
\end{eqnarray}
インダクタ\(L\)のリアクタンス\(X_L\)は\(X_L={\omega}L\)です。一方、コンデンサ\(C\)のリアクタンス\(X_C\)は\(X_C=\displaystyle\frac{1}{{\omega}C}\)です。(14)式から分かるように、共振角周波数\({\omega}_0\)では「インダクタ\(L\)のリアクタンス\(X_L\)」と「コンデンサ\(C\)のリアクタンス\(X_C\)」が等しくなります。
共振角周波数\({\omega}_0\)の時、RLC並列回路に流れる電流の大きさ\(I\)が最小値\(I_{MIN}\)となり、\(I_{MIN}\)は次式となります。
\begin{eqnarray}
I_{MIN}&=&V\sqrt{\left(\frac{1}{R}\right)^2+\left({\omega}_0C-\displaystyle\frac{1}{{\omega}_0L}\right)^2}\\
\\
&=&V\sqrt{\left(\frac{1}{R}\right)^2+0^2}\\
\\
&=&\frac{V}{R}\tag{15}
\end{eqnarray}
ここで、(3)式と(15)式を見て見ると、\(I_R\)と\(I_{MIN}\)が同じ値になっていることが分かります。すなわち、(9)式と(10)式は次式に変形することができます。
\begin{eqnarray}
I_L&=&Q×I_R=Q×I_{MIN}\tag{16}\\
\\
I_C&=&Q×I_R=Q×I_{MIN}\tag{17}
\end{eqnarray}
したがって、Q値は共振時において(共振角周波数\({\omega}_0\)の時において)、電源から流れる電流の大きさ\(I_{MIN}\)の何倍の電流がインダクタ\(L\)またはコンデンサ\(C\)に流れているかを表す値でもあります。Q値が大きければ大きいほど、インダクタ\(L\)とコンデンサ\(C\)に流れる電流が大きくなります。
まとめ
この記事では『RLC並列共振回路』について、以下の内容を説明しました。
- RLC並列共振回路のQ値とは
- RLC並列共振回路のQ値の「導出方法」
- 「Q値」と「インダクタ\(L\)とコンデンサ\(C\)に流れる電流」の関係
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






