電気の流れを妨げるものとして、『抵抗(レジスタンス)』と『リアクタンス』と『インピーダンス』があります。
これらの用語の違いをご存知でしょうか。
この記事では『抵抗(レジスタンス)』と『リアクタンス』と『インピーダンス』の定義と違いについて、式や図を用いて分かりやすく説明しています。ご参考になれば幸いです。
『抵抗(レジスタンス)』と『リアクタンス』と『インピーダンス』の違い
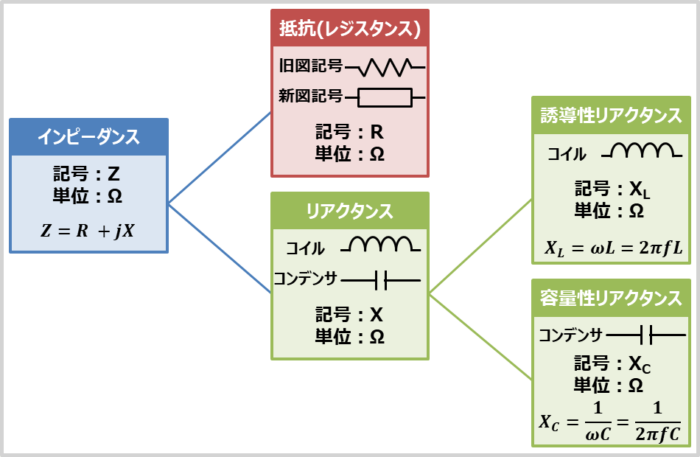
最初に『抵抗(レジスタンス)』と『リアクタンス』と『インピーダンス』の違いを下記にまとめます。後ほど各用語について詳しく説明します。
- 抵抗(レジスタンス)
- リアクタンス
- インピーダンス
直流と交流両方の電気の流れを妨げるものです。記号は「R」を用います。単位は[Ω]です。
交流のみ電気の流れを妨げるものです。記号は「X」を用います。単位は[Ω]です。
『抵抗(レジスタンス)』と『リアクタンス』を合わせたものです。記号は「Z」を用います。単位は[Ω]です。
抵抗(レジスタンス)とは

抵抗(レジスタンス)は直流と交流両方の電気の流れ(電流)を妨げるものです。電気抵抗やレジスタンスとも呼ばれています。
電流を妨げる電気部品で有名なのが「抵抗器」です。一般的に「抵抗」というと「抵抗器」のことを指します。抵抗の図記号を上図に示します。以前は「ギザギザの図記号」が当たり前でしたが、現在では「長方形の図記号」が使われています。
抵抗の記号と単位は下記のようになっています。
- 抵抗の記号
- 抵抗の単位
抵抗は英語では「Resistance(レジスタンス)」と書きます。そのため、抵抗の記号は「Resistance」の頭文字の「R」を用います。
抵抗の単位は[Ω](←オームと読む)になります。
また、抵抗には下記の特徴があります。
抵抗の特徴
- 抵抗が大きいほど電流を妨げる力が大きい
- 抵抗は周波数によって変化しない
これらの特徴を次に説明します。
抵抗が大きいほど電流を妨げる力が大きい
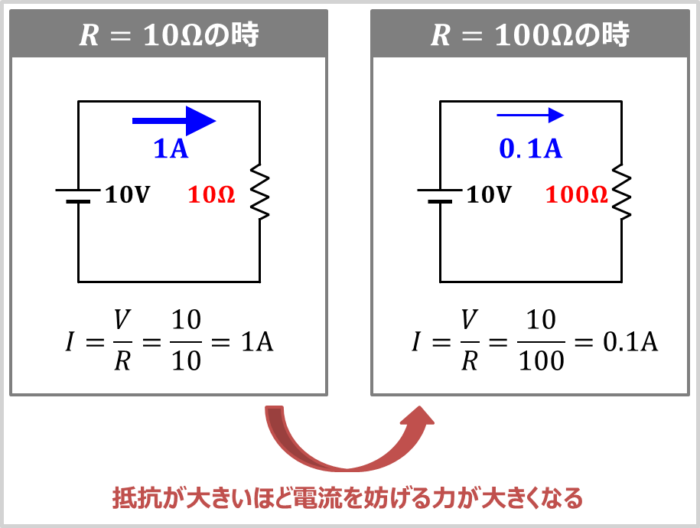
10Vの電池に10Ωの抵抗を接続すると、オームの法則より1Aの電流が流れます。100Ωの抵抗を接続すると、0.1Aの電流が流れます。式で表すと下記となります。
- 10Vの電池に10Ωの抵抗を接続した場合
- 10Vの電池に100Ωの抵抗を接続した場合
\begin{eqnarray}
I=\frac{V}{R}=\frac{10}{10}=1{\mathrm{A}}
\end{eqnarray}
\begin{eqnarray}
I=\frac{V}{R}=\frac{10}{100}=0.1{\mathrm{A}}
\end{eqnarray}
つまり、抵抗値が10倍(10Ω→100Ω)になると、流れる電流は1/10(1A→0.1A)になります。このように、抵抗が大きいほど電流を妨げる力が大きくなります。
抵抗は周波数によって変化しない
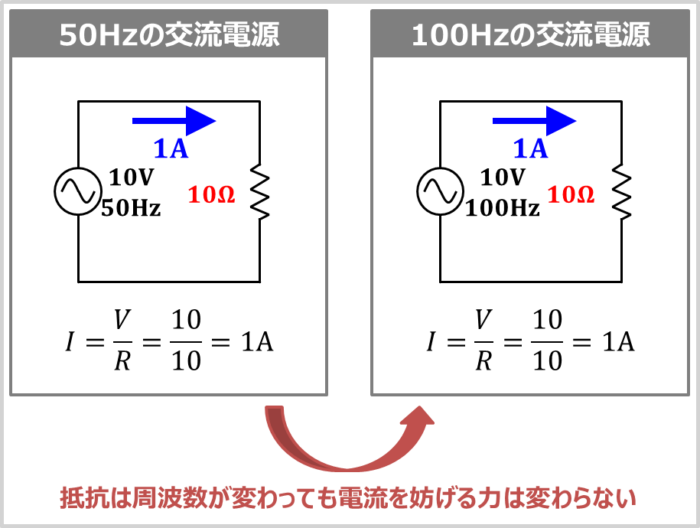
10Ωの抵抗に「振幅10V,周波数50Hzの交流電源」を接続すると、オームの法則より振幅1Aの電流が流れます。周波数を2倍にした「振幅10V,周波数100Hzの交流電源」を接続しても、電流の大きさは1Aのまま変化しません。式で表すと下記となります。
- 10Ωの抵抗に「振幅10V,周波数50Hzの交流電源」を接続した場合
- 10Ωの抵抗に「振幅10V,周波数100Hzの交流電源」を接続した場合
\begin{eqnarray}
I=\frac{V}{R}=\frac{10}{10}=1{\mathrm{A}}
\end{eqnarray}
\begin{eqnarray}
I=\frac{V}{R}=\frac{10}{10}=1{\mathrm{A}}
\end{eqnarray}
このように、抵抗は周波数が変わっても電流を妨げる力は変わらないのです。なお、この後に説明する「リアクタンス」と「インピーダンス」は周波数が変わると電流を妨げる力が変わります。
【補足】導体と絶縁体
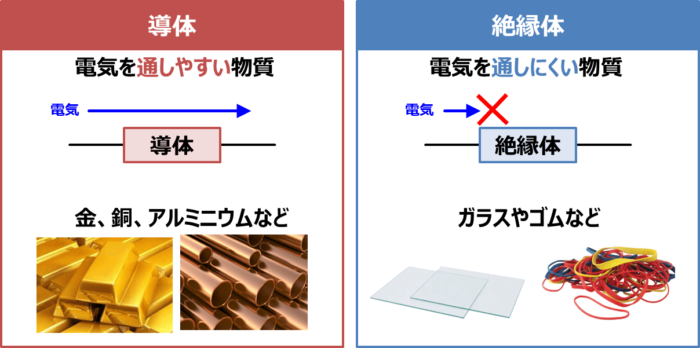
抵抗の大きさにより物質を導体と絶縁体に分類することができます。
- 導体
- 絶縁体
金、銅、アルミニウムなど電気を通しやすい物質(抵抗値が小さい物質)を「導体」といいます。
ガラス、ゴムなど電気を通しにくい物質(抵抗値が大きい物質)を「絶縁体」といいます。
導体と絶縁体について詳しくは下記の記事に記載していますので、ご参考になれば幸いです。
-

【導体と絶縁体の違い】特徴・物質例・静電気対策など!
続きを見る
【補足】抵抗の図記号が「ギザギザ」から「長方形」に変わった理由
抵抗の図記号は規格によって決まっています。
ギザギザの図記号は1952年4月に制定された旧規格(JIS C0301)で決まっていました。しかし、現在は新規格(JIS C 0617)が制定されており、新規格では抵抗の図記号は長方形となっています。なお、当記事では「ギザギザの図記号」を用いています(私がギザギザの方が好きなので^^)。
リアクタンスとは
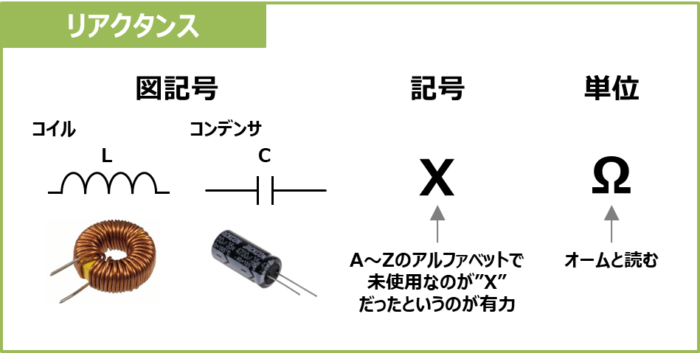

リアクタンスは交流のみ電気の流れ(電流)を妨げるものです。抵抗は交流の周波数が変わっても変化しませんが、リアクタンスは周波数によって変化します。
直流回路においては、電流を妨げるものは「抵抗器」が一般的です。一方、交流回路において、電流の流れを妨げるものは「抵抗器」に加えて「コイル(インダクタ)」と「コンデンサ(キャパシタ)」も含まれます。
このコイルとコンデンサの抵抗成分がリアクタンスとなります。なお、コイルのリアクタンスを「誘導性リアクタンス」といい、コンデンサのリアクタンスを「容量性リアクタンス」といいます。
リアクタンスの記号と単位は下記のようになっています。
- リアクタンスの記号
- リアクタンスの単位
リアクタンスは英語では「Reactance」と書きますが、記号は「R」ではなく「X」を用います。「R」は抵抗の記号ですでに用いられているため使用することができないからです。A~Zのアルファベットのうち使用されていなかったものが「X」なので、リアクタンスの記号が「X」になったというのが有力です。
リアクタンスの単位は抵抗と同じく[Ω](←オームと読む)になります。
また、リアクタンスには下記の特徴があります。
リアクタンスの特徴
- リアクタンスが大きいほど電流を妨げる力が大きい
- リアクタンスは周波数によって変化する
これらの特徴を次に説明します。
リアクタンスが大きいほど電流を妨げる力が大きい
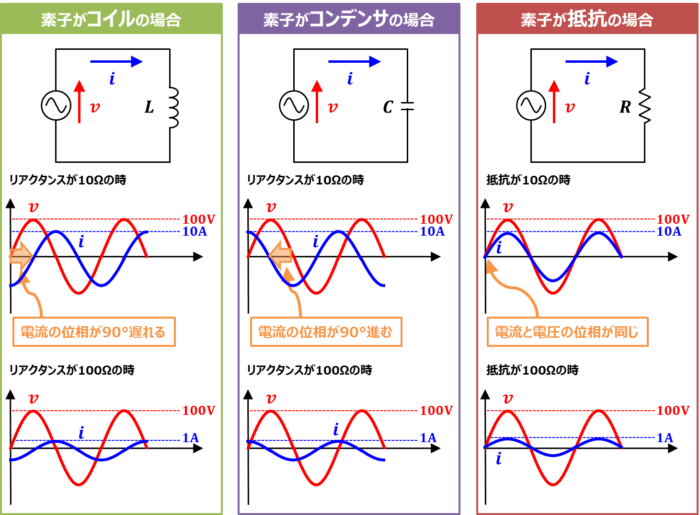

100Vの交流電源にリアクタンスが10Ωの素子を接続すると、オームの法則より1Aの電流が流れます。リアクタンスが100Ωの素子を接続すると、1Aの電流が流れます。式で表すと下記となります。
- 100Vの交流電源にリアクタンスが10Ωの素子を接続した場合
- 100Vの交流電源にリアクタンスが100Ωの素子を接続した場合
\begin{eqnarray}
I=\frac{V}{X}=\frac{100}{10}=10{\mathrm{A}}
\end{eqnarray}
\begin{eqnarray}
I=\frac{V}{X}=\frac{100}{100}=1{\mathrm{A}}
\end{eqnarray}
つまり、リアクタンスが10倍(10Ω→100Ω)になると、流れる電流は1/10(10A→1A)になります。このように、リアクタンスが大きいほど電流を妨げる力が大きくなります。
なお、交流には位相があります。素子がコイルやコンデンサの場合、電圧と電流の位相にずれが生じます。
- 素子がコイルの場合
- 素子がコンデンサの時
- 素子が抵抗の時
電圧の位相に対して電流の位相が90°遅れます。
電圧の位相に対して電流の位相が90°進みます。
電圧と電流の位相は同じです。
リアクタンスは周波数によって変化する
リアクタンスは周波数によって変化します。
- コイルのリアクタンス(誘導性リアクタンス)
- コンデンサのリアクタンス(容量性リアクタンス)
周波数に比例します。
周波数に反比例します。
次に各リアクタンスについて順番に説明します。
コイルのリアクタンス(誘導性リアクタンス)


コイルのリアクタンスXLは次式で表されます。
\begin{eqnarray}
X_L={\omega}L=2{\pi}fL
\end{eqnarray}
\({\omega}\):角周波数(\({\omega}=2{\pi}f\))[rad/s]
\(f\):周波数[Hz]
\(L\):コイルのインダクタンス[H](←ヘンリーと読みます)
上式より誘導性リアクタンスは周波数に比例します。そのため、交流回路の周波数が高いほど、誘導性リアクタンスは大きくなります。なお、直流回路では周波数は0Hzなので誘導性リアクタンスは0Ωとなります(コイルを短絡するのと同じ)。
コンデンサのリアクタンス(容量性リアクタンス)


コンデンサのリアクタンスXCは次式で表されます。
\begin{eqnarray}
X_C=\frac{1}{{\omega}C}=\frac{1}{2{\pi}fC}
\end{eqnarray}
\({\omega}\):角周波数(\({\omega}=2{\pi}f\))[rad/s]
\(f\):周波数[Hz]
\(C\):コンデンサの静電容量[F](←ファラドと読みます)
上式より容量性リアクタンスは周波数に反比例します。そのため、交流回路の周波数が高いほど、容量性リアクタンスは小さくなります。なお、直流回路では周波数は0Hzなので容量性リアクタンスは無限大となります(コンデンサを開放するのと同じ)。
インピーダンスとは
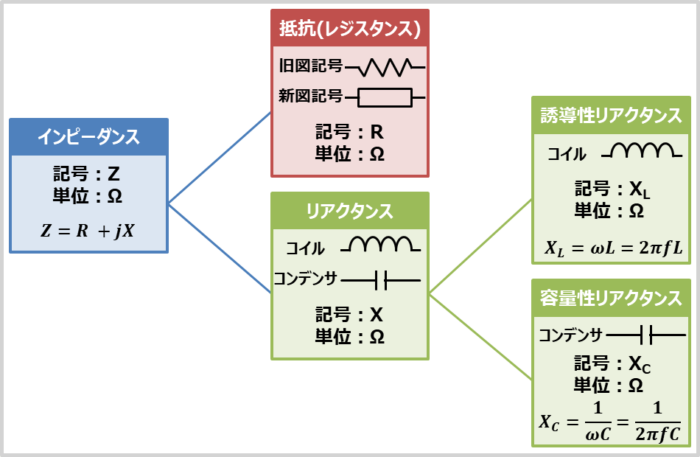

インピーダンスは『抵抗(レジスタンス)』と『リアクタンス』を合わせたものです。
少し言い方を変えると、電流を妨げるものの総称が『インピーダンス』であり、インピーダンスの中で直流も交流も電流を妨げるものが『抵抗(レジスタンス)』であり、交流のみ電流を妨げるものが『リアクタンス』ということになります。
また、インピーダンスを式で表すと下記の式で表されます。
\begin{eqnarray}
Z=R+jX
\end{eqnarray}
そのため、インピーダンスの実数部が『抵抗(レジスタンス)』、虚数部が『リアクタンス』と説明している資料も多いです。
インピーダンスの記号と単位は下記となっています。
- インピーダンスの記号
- インピーダンスの単位
インピーダンスは英語では「Impedance」と書きますが、記号は「I」ではなく「Z」を用います。「I」は電流の記号ですでに用いられているため使用することができないからです。A~Zのアルファベットのうち使用されていなかったものが「Z」なので、インピーダンスの記号が「Z」になったというのが有力です。
インピーダンスの単位は抵抗と同じく[Ω](←オームと読む)になります。
まとめ
この記事では『抵抗(レジスタンス)』と『リアクタンス』と『インピーダンス』について、以下の内容を説明しました。
- 『抵抗(レジスタンス)』と『リアクタンス』と『インピーダンス』の違い
- 『抵抗(レジスタンス)』とは
- 『リアクタンス』とは
- 『インピーダンス』とは
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。