ベクトルの表し方には『直交座標表示』と『極座標表示』があります。
この記事にはこれらの表示方法について、
- 『直交座標表示』の意味と特徴
- 『極座標表示』の意味と特徴
- 『直交座標表示』と『極座標表示』の変換方法
などを図を用いて分かりやすく解説しています。
直交座標表示とは
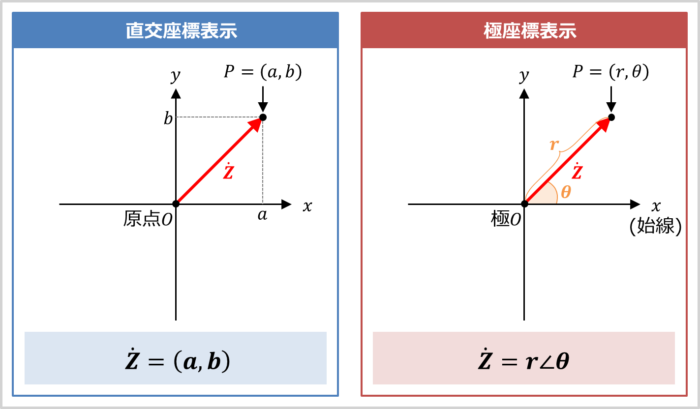
直交座標表示はベクトルを『横軸のx成分』と『縦軸のy成分』で表す表示方法です(上図の左参照)。
点\(P(a,b)\)は『原点\(O\)を出発点として、x軸方向に\(a\)、y軸方向に\(b\)だけ移動した場所』を意味しています。
ここで、『原点\(O\)』と『点\(P(a,b)\)』を結んだベクトル\({\dot{Z}}\)がある時、ベクトル\({\dot{Z}}\)は直交座標表示では次のように表されます。
\begin{eqnarray}
{\dot{Z}}=(a,b)
\end{eqnarray}
極座標表示とは
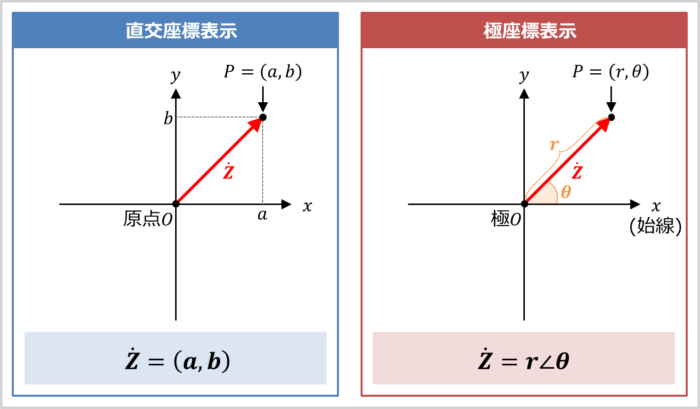
極座標表示はベクトルを『原点からの距離』と『ベクトルとx軸のなす角\({\theta}\)(偏角\({\theta}\))』で表す表示方法です(上図の右参照)。なお、極座標では、原点\(O\)を極\(O\)と呼び、x軸を始線と呼びます。
点\(P(r,{\theta})\)は『極\(O\)を出発点として、始線から\({\theta}{\mathrm{[rad]}}\)回転し、距離\(r\)伸ばした場所』を意味しています。
ここで、『極\(O\)』と『点\(P(r,{\theta})\)』を結んだベクトル\({\dot{Z}}\)がある時、ベクトル\({\dot{Z}}\)は極座標表示では次のように表されます。
\begin{eqnarray}
{\dot{Z}}=r{\angle}{\theta}
\end{eqnarray}
『直交座標表示』と『極座標表示』の変換方法
では次に
- 『直交座標表示のベクトル\({\dot{Z}}=(a,b)\)』を『極座標表示のベクトル\({\dot{Z}}=r{\angle}{\theta}\)』に変換する方法
- 『極座標表示のベクトル\({\dot{Z}}=r{\angle}{\theta}\)』を『直交座標表示のベクトル\({\dot{Z}}=(a,b)\)』に変換する方法
について説明します。
『直交座標表示』から『極座標表示』に変換する方法
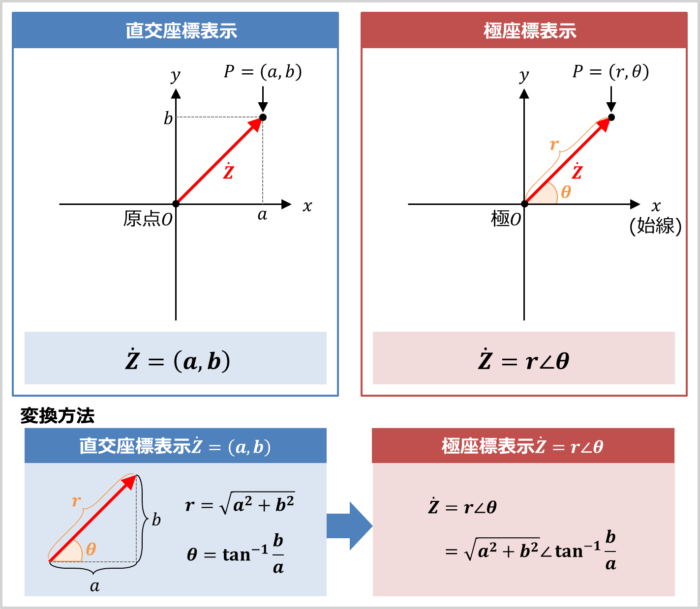
『直交座標表示のベクトル\({\dot{Z}}=(a,b)\)』を極座標表示に変換してみましょう。
繰り返しになりますが、極座標表示はベクトルを『原点からの距離』と『ベクトルとx軸のなす角\({\theta}\)(偏角\({\theta}\))』で表します。
原点からの距離を\(r\)とすると、三平方の定理(ピタゴラスの定理)より、\(r\)と\(a\)と\(b\)の関係は次式で表されます。
\begin{eqnarray}
r=\sqrt{a^2+b^2}
\end{eqnarray}
また、偏角\({\theta}\)は次式で表されます。
\begin{eqnarray}
{\theta}={\tan}^{-1}\frac{b}{a}
\end{eqnarray}
したがって、ベクトル\({\dot{Z}}=(a,b)\)は極座標表示では次式で表すことができます。
\begin{eqnarray}
{\dot{Z}}&=&r{\angle}{\theta}\\
&=&\sqrt{a^2+b^2}{\angle}{\tan}^{-1}\frac{b}{a}
\end{eqnarray}
『極座標表示』から『直交座標表示』に変換する方法
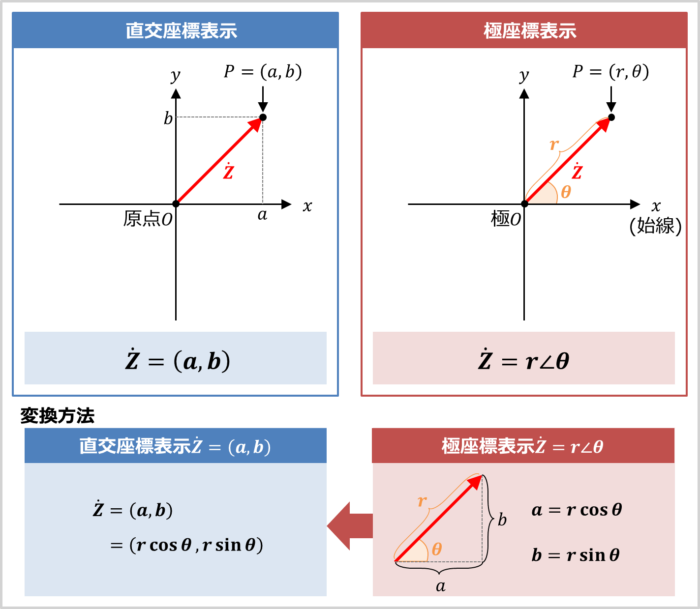
『極座標表示のベクトル\({\dot{Z}}=r{\angle}{\theta}\)』を直交座標表示に変換してみましょう。
繰り返しになりますが、直交座標表示はベクトルを『横軸のx成分』と『縦軸のy成分』で表します。
x成分の座標を\(a\)、y成分の座標を\(b\)とすると、\(a\)と\(b\)と\(r\)の関係は次式で表されます。
\begin{eqnarray}
a&=&r{\cos}{\theta}\\
b&=&r{\sin}{\theta}
\end{eqnarray}
したがって、ベクトル\({\dot{Z}}=r{\angle}{\theta}\)は直交座標表示では次式で表すことができます。
\begin{eqnarray}
{\dot{Z}}&=&(a,b)\\
&=&(r{\cos}{\theta},r{\sin}{\theta})
\end{eqnarray}
複素平面について
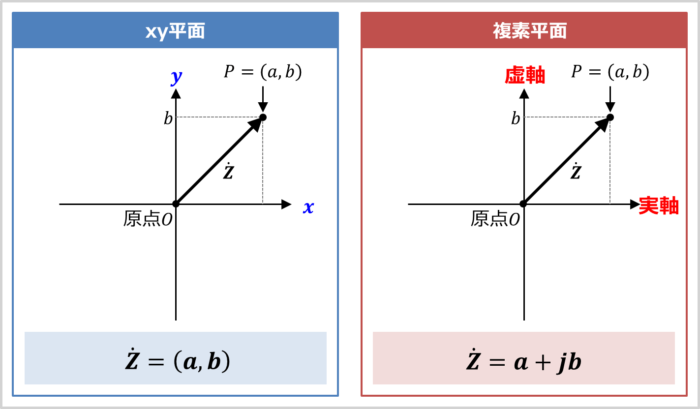
今まではxy平面上にあるベクトルの『直交座標表示』と『極座標表示』について説明しました。
では次に、複素平面上にあるベクトルの『直交座標表示』と『極座標表示』について説明します。複素平面のx軸を実軸, y軸を虚軸といいます。
複素数の直交座標表示とは
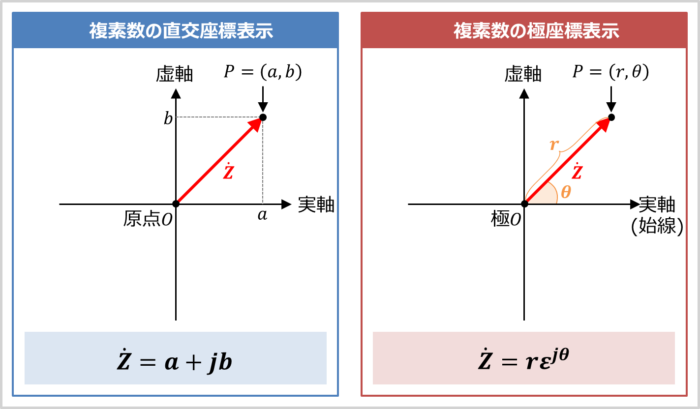
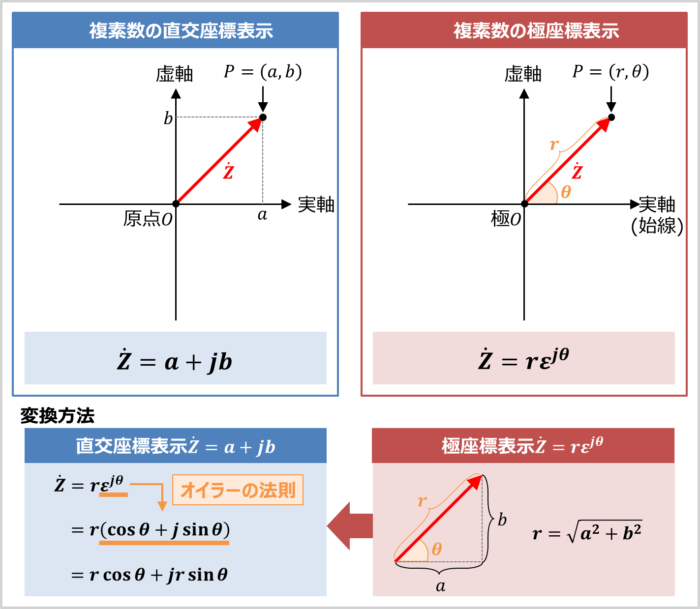
複素数の直交座標表示はベクトルを『(実部)+j(虚部)』で表す表示方法です(上図の左参照)。『(実部)+j(虚部)』は実軸と虚軸の成分で表されています。
点\(P(a,b)\)は『原点\(O\)を出発点として、実軸方向に\(a\)、虚軸方向に\(b\)だけ移動した場所』を意味しています。
ここで、『原点\(O\)』と『点\(P(a,b)\)』を結んだベクトル\({\dot{Z}}\)がある時、ベクトル\({\dot{Z}}\)は複素数の直交座標表示では次のように表されます。
\begin{eqnarray}
{\dot{Z}}=a+jb
\end{eqnarray}
補足
下記の式のように、ベクトル\({\dot{Z}}\)をxy平面における直交座標表示のように表している場合もあります。
\begin{eqnarray}
{\dot{Z}}=(a,b)
\end{eqnarray}
複素数の極座標表示とは
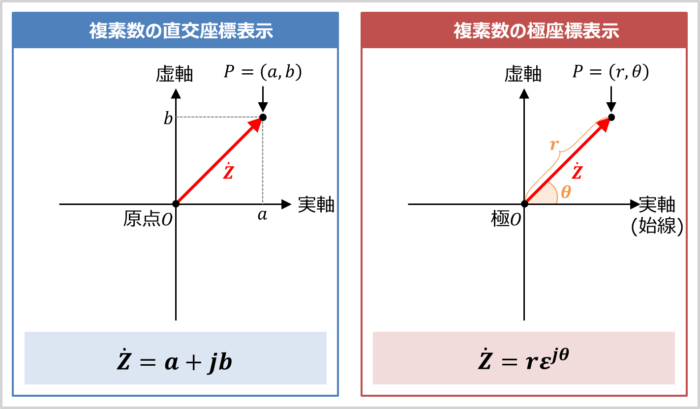
極座標表示はベクトルを『原点からの距離』と『ベクトルと実軸のなす角\({\theta}\)(偏角\({\theta}\))』で表す表示方法です(上図の右参照)。なお、極座標では、原点\(O\)を極\(O\)と呼び、実軸を始線と呼びます。
点\(P(r,{\theta})\)は『極\(O\)を出発点として、始線から\({\theta}{\mathrm{[rad]}}\)回転し、距離\(r\)伸ばした場所』を意味しています。
ここで、『極\(O\)』と『点\(P(r,{\theta})\)』を結んだベクトル\({\dot{Z}}\)がある時、ベクトル\({\dot{Z}}\)は極座標表示では次のように表されます。
\begin{eqnarray}
{\dot{Z}}=r{\varepsilon}^{j{\theta}}
\end{eqnarray}
上式において\({\varepsilon}\)(イプシロン)は自然対数の底と言われる定数であり、以下の値を持ちます。
\begin{eqnarray}
{\varepsilon}=2.71828{\cdots}
\end{eqnarray}
なお、通常は(数学の世界では)自然対数の底は『\(e\)』で表しますが、電気の世界では『\(e\)』は起電力の記号として用いられているので、『\({\varepsilon}\)』を用います。
補足
- 下記の式のように、ベクトル\({\dot{Z}}\)をxy平面における極座標表示のように表している場合もあります。
\begin{eqnarray}
{\dot{Z}}=r{\angle}{\theta}
\end{eqnarray} - ベクトル\({\dot{Z}}=r{\varepsilon}^{j{\theta}}\)は、複素数を指数関数を用いて『原点からの距離\(r\)』と『偏角\({\theta}\)』で表わした形です。このような式は『(指数関数による)極形式』と呼ばれています。
『直交座標表示』と『極座標表示』の変換方法(複素数の場合)
では次に
- 『直交座標表示のベクトル\({\dot{Z}}=a+jb\)』を『極座標表示のベクトル\({\dot{Z}}=r{\varepsilon}^{j{\theta}}\)』に変換する方法
- 『極座標表示のベクトル\({\dot{Z}}=r{\varepsilon}^{j{\theta}}\)』を『直交座標表示のベクトル\({\dot{Z}}=a+jb\)』に変換する方法
について説明します。
『直交座標表示』から『極座標表示』に変換する方法(複素数の場合)
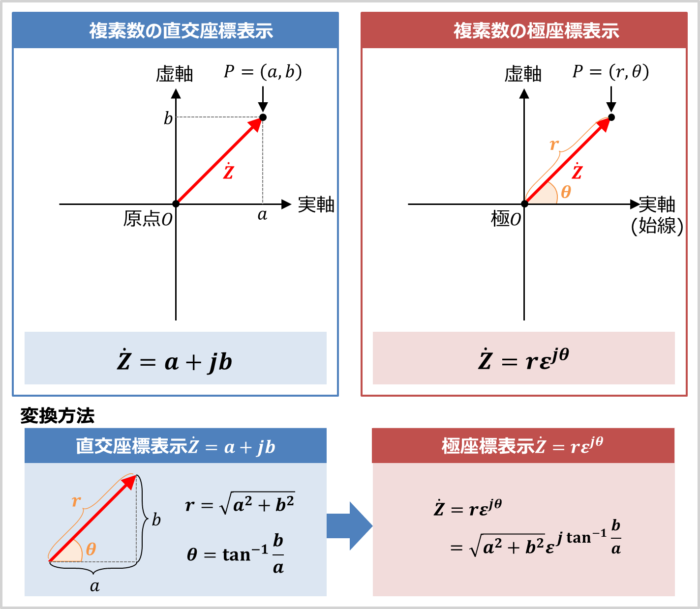
『直交座標表示のベクトル\({\dot{Z}}=a+jb\)』を極座標表示に変換してみましょう。
繰り返しになりますが、極座標表示はベクトルを『原点からの距離』と『ベクトルと実軸のなす角\({\theta}\)(偏角\({\theta}\))』で表します。
原点からの距離を\(r\)とすると、三平方の定理(ピタゴラスの定理)より、\(r\)と\(a\)と\(b\)の関係は次式で表されます。
\begin{eqnarray}
r=\sqrt{a^2+b^2}
\end{eqnarray}
また、偏角\({\theta}\)は次式で表されます。
\begin{eqnarray}
{\theta}={\tan}^{-1}\frac{b}{a}
\end{eqnarray}
したがって、ベクトル\({\dot{Z}}=a+jb\)は極座標表示では次式で表すことができます。
\begin{eqnarray}
{\dot{Z}}&=&r{\varepsilon}^{j{\theta}}\\
&=&\sqrt{a^2+b^2}{\varepsilon}^{j{\;}{\displaystyle\tan}^{-1}\displaystyle\frac{b}{a}}
\end{eqnarray}
『極座標表示』から『直交座標表示』に変換する方法(複素数の場合)
『極座標表示のベクトル\({\dot{Z}}=r{\varepsilon}^{j{\theta}}\)』を直交座標表示に変換してみましょう。
繰り返しになりますが、直交座標表示はベクトルを『(実部)+j(虚部)』で表します。
実軸成分の座標を\(a\)、虚軸成分の座標を\(b\)とすると、三平方の定理(ピタゴラスの定理)より、\(r\)と\(a\)と\(b\)の関係は次式で表されます。
\begin{eqnarray}
r=\sqrt{a^2+b^2}
\end{eqnarray}
また、『\({\varepsilon}^{j{\theta}}\)』はオイラーの法則より次式が成り立ちます。
\begin{eqnarray}
{\varepsilon}^{j{\theta}}={\cos}{\theta}+j{\sin}{\theta}
\end{eqnarray}
したがって、ベクトル\({\dot{Z}}=r{\varepsilon}^{j{\theta}}\)は直交座標表示では次式で表すことができます。
\begin{eqnarray}
{\dot{Z}}&=&rεjθ\\
&=&r({\cos}{\theta}+j{\sin}{\theta})\\
&=&r{\cos}{\theta}+jr{\sin}{\theta}
\end{eqnarray}
補足
- ベクトル\({\dot{Z}}=r({\cos}{\theta}+j{\sin}{\theta})\)は、複素数を三角関数を用いて『原点からの距離\(r\)』と『偏角\({\theta}\)』で表わした形です。このような式は『(三角関数による)極形式』と呼ばれています。
まとめ
この記事では『直交座標表示』と『極座標表示』について、以下の内容を説明しました。
- 『直交座標表示』の意味と特徴
- 『極座標表示』の意味と特徴
- 『直交座標表示』と『極座標表示』の変換方法
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






