この記事ではRC回路の時定数について
- 時定数の重要ポイント
- 時定数τ=CRの求め方
- 時定数の単位が[s]となる理由
などを図を用いて分かりやすく説明しています。
RC回路の時定数
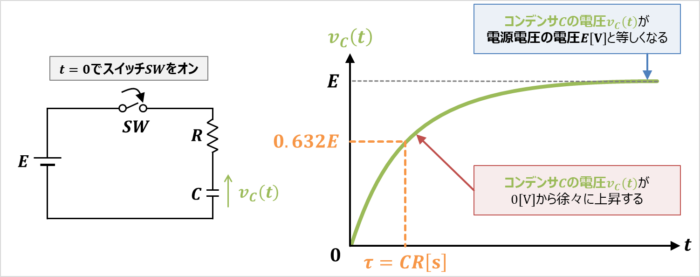
上図は抵抗\(R{\mathrm{[Ω]}}\)、コンデンサ\(C{\mathrm{[F]}}\)、直流電源\(E{\mathrm{[V]}}\)、スイッチ\(SW\)からなるRC回路です。
上図のRC回路において、『\(t=0{\mathrm{[s]}}\)』でスイッチ\(SW\)をONにすると、以下の過渡現象が生じます。
過渡現象
- コンデンサ\(C\)の電圧\(v_{C}(t)\)が\(0{\mathrm{[V]}}\)から徐々に上昇する。
- ある程度時間が経過すると、コンデンサ\(C\)の電圧\(v_{C}(t)\)が電源電圧の電圧\(E{\mathrm{[V]}}\)と等しくなる。
ここで、時定数のポイントについてまとめます(後で図を用いて分かりやすく説明します)。
時定数のポイント
- 時定数とは、過渡現象がどのくらい続くのかを表す目安を表しており、単位は[s]となります。
- 時定数は、ギリシャ文字の\({\tau}\)(タウ)で表されます。
- RC回路の時定数\({\tau}\)は、コンデンサCと抵抗Rの積となり『\({\tau}=CR\)』となります。
- 時間\(t\)が『時定数\({\tau}(=CR)\)』となった時、コンデンサ\(C\)の電圧\(v_{C}(t)\)は『\(0.632E\)』となります。
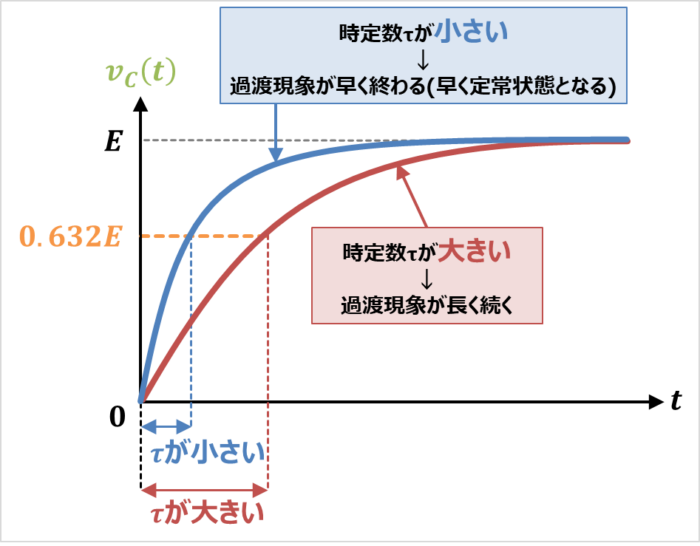
- 時定数\({\tau}\)が大きいと過渡現象が長く続き、小さいと過渡現象が早く終わります(早く定常状態になります)。
・・・少しイメージが難しいですね。ではこれから図を用いて分かりやすく時定数のポイントを説明していきます。
もう少し詳しく!
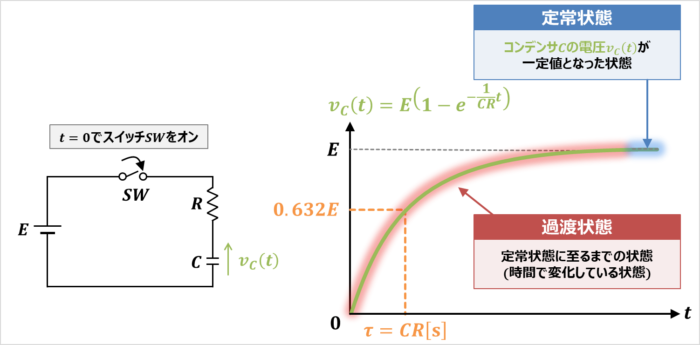
繰り返しになりますが、上図のRC回路において、『\(t=0{\mathrm{[s]}}\)』でスイッチ\(SW\)をONにすると、コンデンサ\(C\)の電圧\(v_{C}(t)\)が\(0{\mathrm{[V]}}\)から徐々に上昇し、ある程度時間が経過すると、コンデンサ\(C\)の電圧\(v_{C}(t)\)が電源電圧の電圧\(E{\mathrm{[V]}}\)と等しくなります。
この時、コンデンサ\(C\)の電圧\(v_{C}(t)\)が変化せず一定値(\(E{\mathrm{[V]}}\))となった状態を「定常状態」、「定常状態」に至るまでの状態を「過渡状態」、その過程で見られる現状を「過渡現象」といいます。
また、このコンデンサ\(C\)の電圧\(v_{C}(t)\)を式で表すと次式で表されます。
\begin{eqnarray}
v_{C}(t)=E\left(1-e^{-\frac{1}{CR}t}\right)\tag{1}
\end{eqnarray}
なお、(1)式の導出については、以下の記事で説明しています。導出方法について知りたい方は以下の記事を参考にしてください。
-

【RC直列回路の微分方程式】『過渡現象』の解き方!
続きを見る
(1)式より、コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が『時定数\({\tau}(=CR)\)』となった時、次式となります。
\begin{eqnarray}
v_{C}({\tau})&=&E\left(1-e^{-\frac{1}{CR}×CR}\right)\\
&=&E\left(1-e^{-1}\right)\\
&=&E\left(1-\frac{1}{e}\right)\tag{2}
\end{eqnarray}
ここで、(2)式に出てくる\(e\)は自然定数\(\log_{e}\)の底であり、ネイピア数と呼ばれるものです。ネイピア数\(e\)の値は次式で表されます。
\begin{eqnarray}
e=2.71828{\;}18284{\;}59045{\;}23536{\;}{\cdots}\tag{3}
\end{eqnarray}
このネイピア数\(e\)を(2)式に代入すると、次式となります。
\begin{eqnarray}
v_{C}({\tau})&=&E\left(1-\frac{1}{e}\right)\\
&{\approx}&E\left(1-\frac{1}{2.71828{\;}{\cdots}}\right)\\
&{\approx}&E\left(1-0.368\right)\\
&{\approx}&0.632E\tag{4}
\end{eqnarray}
つまり、コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が『時定数\({\tau}(=CR)\)』となった時、電源電圧の電圧\(E\)の\(63.2{\%}\)となります。
言い換えると、定常状態における電圧値(電源電圧の電圧\(E\))の\(63.2{\%}\)に達するまでの時間が時定数\({\tau}\)ということになります。
また、(4)式より『時定数\({\tau}(=CR)\)』の大きさによって以下のことが分かります。
- 『時定数\({\tau}=CR\)』が大きい時
- 『時定数\({\tau}=CR\)』が小さい時
コンデンサ\(C\)の電圧\(v_{C}(t)\)が\(0.632E\)になるのに時間がかかる。つまり、過渡現象が長く続く。
コンデンサ\(C\)の電圧\(v_{C}(t)\)が早く\(0.632E\)になる。つまり、過渡現象が早く終わる(早く定常状態となる)。

補足
- 時定数は英語では「Time Constant」と書きます。
- 時定数は一般的には「じていすう」と読みます。しかし、JISでは時定数の日本語の読み方は「ときじょうすう」であると定められてます。また、「Time Constant」の邦訳語としては「ときていすう」なので「ときていすう」と読む人もいます。
RC回路の時定数の求め方
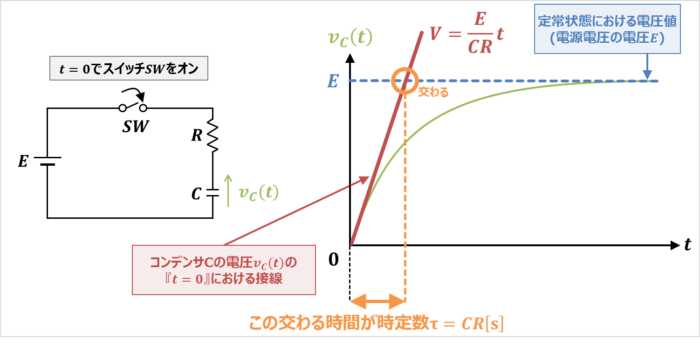

RC回路の時定数\({\tau}\)が『\({\tau}=CR\)』となるのはなぜでしょうか?
ここではその理由を説明します。
先に結論から言うと・・・
コンデンサ\(C\)の電圧\(v_{C}(t)\)の『\(t=0\)』における接線と定常状態における電圧値(電源電圧の電圧\(E\))の交わる時間が『時定数\({\tau}=CR\)』となるのです。
では実際に導出してみましょう。
繰り返しになりますが、上図のRC回路において、『\(t=0{\mathrm{[s]}}\)』でスイッチ\(SW\)をONにすると、コンデンサ\(C\)の電圧\(v_{C}(t)\)が\(0{\mathrm{[V]}}\)から徐々に上昇し、ある程度時間が経過すると、コンデンサ\(C\)の電圧\(v_{C}(t)\)が電源電圧の電圧\(E{\mathrm{[V]}}\)と等しくなります。
(1)式を\(t\)で微分して、『\(t=0\)』を代入すると、コンデンサ\(C\)の電圧\(v_{C}(t)\)の『\(t=0\)』における接線の傾きを求めることができます。
(1)式を\(t\)で微分すると次式となります。
\begin{eqnarray}
\frac{dv_{C}(t)}{dt}&=&\frac{1}{dt}\left[E\left(1-e^{-\frac{1}{CR}t}\right)\right]\\
&=&\frac{1}{dt}\left(E-Ee^{-\frac{1}{CR}t}\right)\\
&=&E\frac{1}{dt}(1)-E\frac{1}{dt}\left(e^{-\frac{1}{CR}t}\right)\\
&=&Et-E\left(-\frac{1}{CR}\right)e^{-\frac{1}{CR}t}\\
&=&Et+\frac{E}{CR}e^{-\frac{1}{CR}t}\tag{5}
\end{eqnarray}
(5)式に『\(t=0\)』を代入すると、次式となります。
\begin{eqnarray}
\frac{dv_{C}(0)}{dt}&=&E×0+\frac{E}{CR}e^{-\frac{1}{CR}×0}\\
&=&0+\frac{E}{CR}e^{0}\\
&=&\frac{E}{CR}×1\\
&=&\frac{E}{CR}\tag{6}
\end{eqnarray}
つまり、コンデンサ\(C\)の電圧\(v_{C}(t)\)の『\(t=0\)』における接線の傾きは『\(\displaystyle\frac{E}{CR}\)』となります。
コンデンサ\(C\)の電圧\(v_{C}(t)\)の『\(t=0\)』における接線は『\((0,0)\)』を通るので、次式となります。
\begin{eqnarray}
V=\frac{E}{CR}t\tag{7}
\end{eqnarray}
(7)式のコンデンサ\(C\)の電圧\(v_{C}(t)\)の『\(t=0\)』における接線と定常状態における電圧値(電源電圧の電圧\(E\))が交わる時間を求めます。
(7)式の\(V\)に\(E\)を代入すると次式となります。
\begin{eqnarray}
E&=&\frac{E}{CR}t\\
{\Leftrightarrow}t&=&CR\tag{8}
\end{eqnarray}
この時間が時定数となるため、RC回路の時定数\({\tau}\)は『\({\tau}=CR\)』となります。
(8)式から分かるように、RC回路ではコンデンサ\(C\)の容量または抵抗\(R\)の抵抗値が大きくなると、時定数\({\tau}\)が大きくなることが分かります(RC回路の時定数\({\tau}\)はコンデンサ\(C\)の容量と抵抗\(R\)の抵抗値に比例するということです)。
時定数の単位が[s]の理由
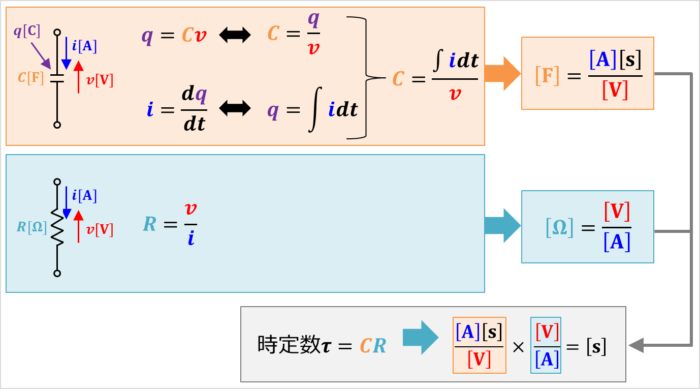

時定数\({\tau}\)の単位が\({\mathrm{[s]}}\)となるのはなぜでしょうか?
例えば、RC回路の場合、コンデンサ\(C\)の静電容量の単位は\({\mathrm{[F]}}\)、抵抗\(R\)の抵抗値の単位は\({\mathrm{[Ω]}}\)なのに、なぜ時定数\({\tau}=CR\)の単位は\({\mathrm{[s]}}\)となるのでしょうか?
ここではその理由を説明します。
コンデンサ\(C\)の静電容量の単位と抵抗\(R\)の抵抗値の単位について別々に詳しく見ていきます。
コンデンサCの静電容量の単位について
コンデンサ\(C\)に蓄えられる電荷\(q{\mathrm{[C]}}\)とコンデンサにかかる電圧\(v{\mathrm{[V]}}\)とコンデンサの静電容量\(C{\mathrm{[F]}}\)の関係は次式で表されます。
\begin{eqnarray}
q&=&Cv\\
{\Leftrightarrow}C&=&\frac{q}{v}\tag{9}
\end{eqnarray}
また、コンデンサ\(C\)に蓄えられる電荷\(q{\mathrm{[C]}}\)とコンデンサに流れる電流\(i{\mathrm{[A]}}\)の関係は次式で表されます。
\begin{eqnarray}
i&=&\frac{dq}{dt}\\
{\Leftrightarrow}q&=&{\displaystyle\int}idt\tag{10}
\end{eqnarray}
(10)式を(9)式に代入すると、次式が得られます。
\begin{eqnarray}
C&=&\frac{q}{v}\\
&=&\frac{{\displaystyle\int}idt}{v}\tag{11}
\end{eqnarray}
(11)式を単位で表すと、次式となります。
\begin{eqnarray}
{\mathrm{[F]}}&=&\frac{{\mathrm{[A]}}{\mathrm{[s]}}}{{\mathrm{[V]}}}\tag{12}
\end{eqnarray}
抵抗Rの抵抗値の単位について
オームの法則より、抵抗\(R\)の抵抗値\(R{\mathrm{[Ω]}}\)と抵抗\(R\)にかかる電圧\(v{\mathrm{[V]}}\)と抵抗\(R\)に流れる電流\(i{\mathrm{[A]}}\)の関係は次式で表されます。
\begin{eqnarray}
R=\frac{v}{i}\tag{13}
\end{eqnarray}
(13)式を単位で表すと、次式となります。
\begin{eqnarray}
{\mathrm{[Ω]}}=\frac{{\mathrm{[V]}}}{{\mathrm{[A]}}}\tag{14}
\end{eqnarray}
つまり、時定数\({\tau}=CR\)を単位は(12)式と(14)式を用いると次式となります。
\begin{eqnarray}
時定数{\tau}の単位&=&{\mathrm{[F]}}×{\mathrm{[Ω]}}\\
&=&\frac{{\mathrm{[A]}}{\mathrm{[s]}}}{{\mathrm{[V]}}}×\frac{{\mathrm{[V]}}}{{\mathrm{[A]}}}\\
&=&{{\mathrm{[s]}}}\tag{15}
\end{eqnarray}
以上より、コンデンサ\(C\)の静電容量の単位と抵抗\(R\)の抵抗値の単位を分解すると、時定数\({\tau}\)の単位が\({\mathrm{[s]}}\)になることが分かります。
RC回路の時定数を2倍、3倍・・・とした時の値
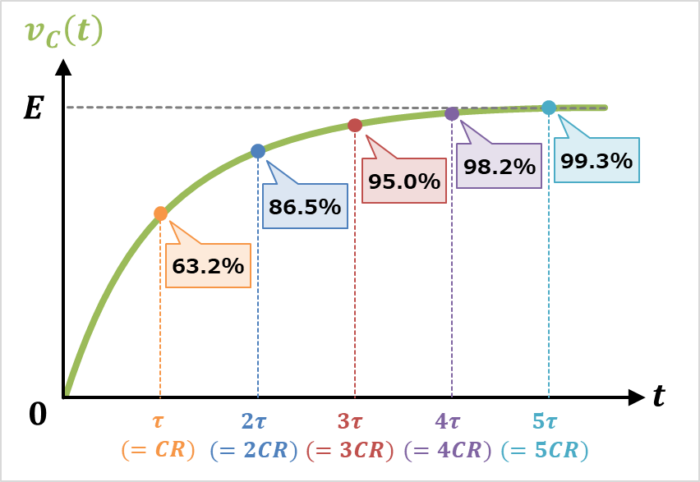

コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が『時定数\({\tau}(=CR)\)』となった時、電源電圧の電圧\(E\)の\(63.2{\%}\)になります。
では、時間\(t\)が時定数\({\tau}\)が2倍の時や3倍の時はコンデンサ\(C\)の電圧\(v_{C}(t)\)はどれくらいになるのでしょうか。
時定数τが1倍の時
時定数\({\tau}\)が1倍の時(つまり、『\(t={\tau}=CR\)』の時)、コンデンサ\(C\)の電圧\(v_{C}(t)\)は以下の値となります。
\begin{eqnarray}
v_{C}({\tau})&=&E\left(1-e^{-\frac{1}{CR}×CR}\right)\\
&=&E\left(1-e^{-1}\right)\\
&=&E\left(1-\frac{1}{e}\right)\\
&{\approx}&E\left(1-\frac{1}{2.71828{\;}{\cdots}}\right)\\
&{\approx}&0.632E\tag{16}
\end{eqnarray}
つまり、コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が時定数\({\tau}\)の1倍の時、電源電圧の電圧\(E\)の\(63.2{\%}\)となります。
時定数τが2倍の時
時定数\({\tau}\)が2倍の時(つまり、『\(t={\tau}=2CR\)』の時)、コンデンサ\(C\)の電圧\(v_{C}(t)\)は以下の値となります。
\begin{eqnarray}
v_{C}(2{\tau})&=&E\left(1-e^{-\frac{1}{CR}×2CR}\right)\\
&=&E\left(1-e^{-2}\right)\\
&=&E\left(1-\frac{1}{e^2}\right)\\
&{\approx}&E\left(1-\frac{1}{2.71828{\;}{\cdots}^2}\right)\\
&{\approx}&0.865E\tag{17}
\end{eqnarray}
つまり、コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が時定数\({\tau}\)の2倍の時、電源電圧の電圧\(E\)の\(86.5{\%}\)となります。
時定数τが3倍の時
時定数\({\tau}\)が3倍の時(つまり、『\(t={\tau}=3CR\)』の時)、コンデンサ\(C\)の電圧\(v_{C}(t)\)は以下の値となります。
\begin{eqnarray}
v_{C}(3{\tau})&=&E\left(1-e^{-\frac{1}{CR}×3CR}\right)\\
&=&E\left(1-e^{-3}\right)\\
&=&E\left(1-\frac{1}{e^3}\right)\\
&{\approx}&E\left(1-\frac{1}{2.71828{\;}{\cdots}^3}\right)\\
&{\approx}&0.950E\tag{18}
\end{eqnarray}
つまり、コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が時定数\({\tau}\)の3倍の時、電源電圧の電圧\(E\)の\(95.0{\%}\)となります。
時定数τが4倍の時
時定数\({\tau}\)が4倍の時(つまり、『\(t={\tau}=4CR\)』の時)、コンデンサ\(C\)の電圧\(v_{C}(t)\)は以下の値となります。
\begin{eqnarray}
v_{C}(4{\tau})&=&E\left(1-e^{-\frac{1}{CR}×4CR}\right)\\
&=&E\left(1-e^{-4}\right)\\
&=&E\left(1-\frac{1}{e^4}\right)\\
&{\approx}&E\left(1-\frac{1}{2.71828{\;}{\cdots}^4}\right)\\
&{\approx}&0.982E\tag{19}
\end{eqnarray}
つまり、コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が時定数\({\tau}\)の4倍の時、電源電圧の電圧\(E\)の\(98.2{\%}\)となります。
時間\(t\)が時定数\({\tau}\)の4倍となると、コンデンサ\(C\)の電圧\(v_{C}(t)\)は定常状態における電圧値(電源電圧の電圧\(E\))の約\(98.2{\%}\)となるので、ほぼ定常状態といえます。
時定数τが5倍の時
時定数\({\tau}\)が5倍の時(つまり、『\(t={\tau}=5CR\)』の時)、コンデンサ\(C\)の電圧\(v_{C}(t)\)は以下の値となります。
\begin{eqnarray}
v_{C}(5{\tau})&=&E\left(1-e^{-\frac{1}{CR}×5CR}\right)\\
&=&E\left(1-e^{-5}\right)\\
&=&E\left(1-\frac{1}{e^5}\right)\\
&{\approx}&E\left(1-\frac{1}{2.71828{\;}{\cdots}^5}\right)\\
&{\approx}&0.993E\tag{20}
\end{eqnarray}
つまり、コンデンサ\(C\)の電圧\(v_{C}(t)\)は時間\(t\)が時定数\({\tau}\)の5倍の時、電源電圧の電圧\(E\)の\(99.3{\%}\)となります。
まとめ
この記事ではRC回路の時定数について、以下の内容を説明しました。
当記事のまとめ
- RC回路の時定数のポイント
- RC回路の時定数の求め方
- 時定数の単位が[s]の理由
- RC回路の時定数τを2倍、3倍・・・とした時の値
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。







