【LLCコンバータ】『伝達関数』と『ゲイン』の導出方法

この記事では『LLCコンバータ』において

LLCコンバータの『伝達関数』と『ゲイン』の導出方法

などを図を用いて分かりやすく説明しています。

基本波近似法(FHA)を用いた伝達関数

LLCコンバータの設計において、解析を単純化するために、2次側の部品を1次側に配置するために、1次換算することが必要となります。この際、基本波近似法(FHA: First Harmonic Approximation)を用います。

この基本波近似法(FHA)によって、負荷抵抗\(R_{OUT}\)を1次換算したものを出力等価AC抵抗\(R_{AC}\)とすると、LLCコンバータは以下の等価回路に変形することができます。

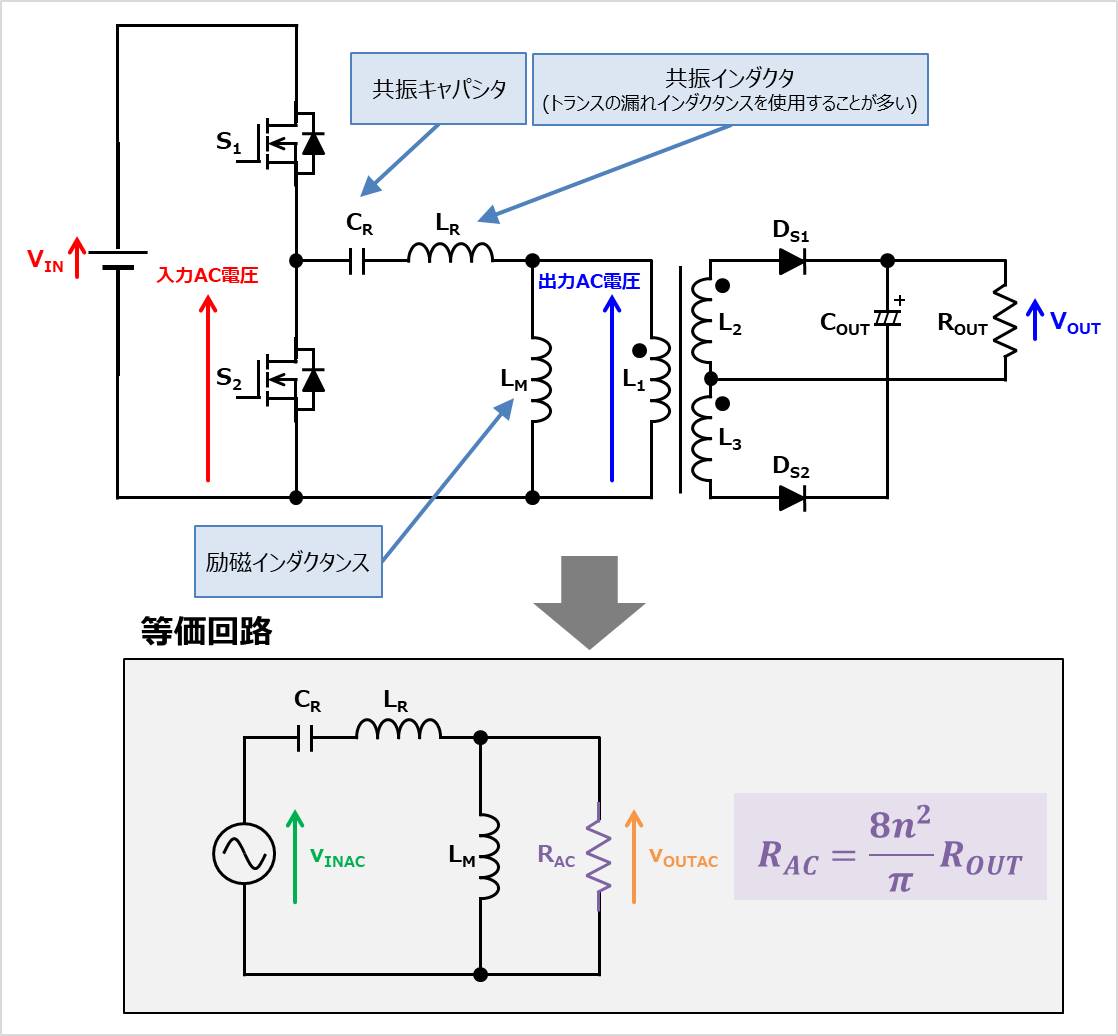
ここで、出力等価AC抵抗\(R_{AC}\)は以下の式で表されます(後ほど導出方法を説明します)。

\begin{eqnarray}
{R_{AC}}=\frac{8n^2}{{\pi}^2} R_{OUT}
\end{eqnarray}

また、LLCコンバータの伝達関数\(M\)はこの等価回路における、「入力AC電圧の基本波成分\(v_{INAC}\)」と「出力AC電圧の基本波成分\(v_{OUTAC}\)」の比率となり、以下の式で表されます。

\begin{eqnarray}
M=\frac{v_{OUTAC}}{v_{INAC}}=\frac{V_{OUT}}{V_{IN}}2n
\end{eqnarray}

では、これから上式の導出方法を説明します。

導出方法

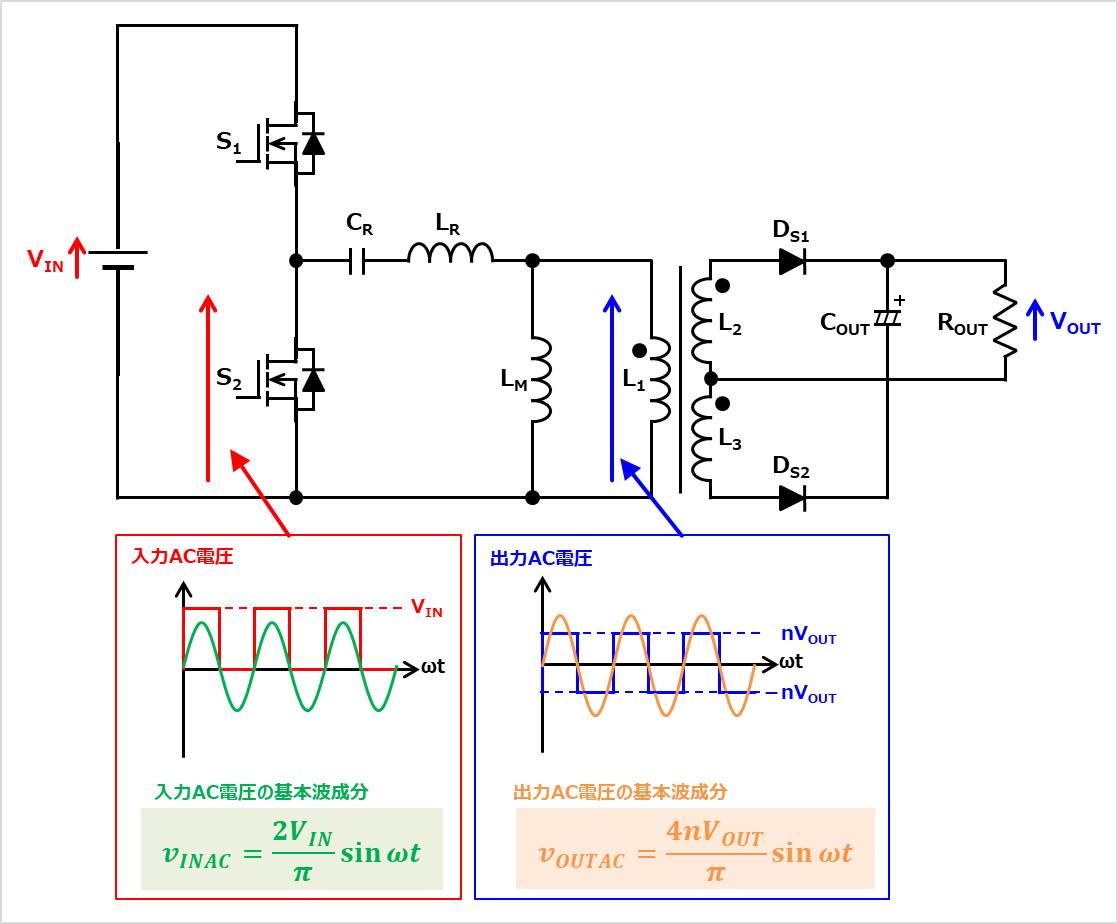
スイッチS1とスイッチS2はデューティ比50%で交互にON/OFFするため、共振キャパシタ\(C_R\)、共振インダクタ\(L_R\)、励磁インダクタ\(L_M\)で構成されている共振タンクの入力AC電圧は振幅\(V_{IN}\)の矩形波となります。この矩形波をフーリエ級数展開した時の基本波成分を\(v_{INAC}\)とすると、入力AC電圧の基本波成分\(v_{INAC}\)は以下の式で表すことができます。
\begin{eqnarray}
v_{INAC}=\frac{2V_{IN}}{{\pi}}{\sin}{\omega}t
\end{eqnarray}
また、入力AC電圧の基本波成分\(v_{INAC}\)の実行値\(V_{INAC(RMS)}\)は以下の式で表すことができます。
\begin{eqnarray}
v_{INAC(RMS)}=\frac{2V_{IN}}{{\sqrt{2}}{\pi}}
\end{eqnarray}

一方、共振タンクの出力AC電圧は励磁インダクタ\(L_M\)にかかる電圧と等しくなります。ここで、巻数比を\(n\)、出力電圧を\(V_{OUT}\)とすると、出力AC電圧は\(-nV_{OUT}\)から\(nV_{OUT}\)まで変化する矩形波となります。この矩形波をフーリエ級数展開した時の基本波成分を\(v_{OUTAC}\)とすると、出力AC電圧の基本波成分\(v_{OUTAC}\)は以下の式で表すことができます。
\begin{eqnarray}
v_{OUTAC}=\frac{4nV_{OUT}}{{\pi}}{\sin}{\omega}t
\end{eqnarray}
また、出力AC電圧の基本波成分\(v_{OUTAC}\)の実行値\(V_{OUTAC(RMS)}\)は以下の式で表すことができます。
\begin{eqnarray}
v_{OUTAC(RMS)}=\frac{4nV_{OUT}}{{\sqrt{2}}{\pi}}
\end{eqnarray}

ここで、「出力抵抗\(R_{OUT}\)の電力損失」と「出力等価AC抵抗\(R_{AC}\)の電力損失」は等しいため、以下の式が成り立ちます。
\begin{eqnarray}
\frac{{V_{OUT}}^2}{R_{OUT}}=\frac{\left(\displaystyle\frac{4nV_{OUT}}{{\sqrt{2}}{\pi}}\right)^2}{R_{AC}}
\end{eqnarray}
上式を整理すると、出力等価AC抵抗\(R_{AC}\)は以下の式で表すことができます。

\begin{eqnarray}
{R_{AC}}=\frac{8n^2}{{\pi}^2} R_{OUT}
\end{eqnarray}

また、「入力AC電圧の基本波成分\(v_{INAC}\)」と「出力AC電圧の基本波成分\(v_{OUTAC}\)」の伝達関数を\(M\)とすると、

\begin{eqnarray}
M&=&\frac{v_{OUTAC}}{v_{INAC}}
&=&\frac{\displaystyle\frac{4nV_{OUT}}{{\pi}}}{\displaystyle\frac{2V_{IN}}{{\pi}}}
&=&\frac{V_{OUT}}{V_{IN}}2n
\end{eqnarray}

となります。上式を整理すると、入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の変換率は以下の式で表すことができます。
\begin{eqnarray}
\frac{V_{OUT}}{V_{IN}}=\frac{M}{2n}
\end{eqnarray}

補足

共振インダクタ\(L_R\)は、一般的には共振インダクタを専用に用意するのではなく、トランスの漏れインダクタンスを利用します。
LLCコンバータの共振タンクの入力電圧と出力電圧は矩形波であり、このままでは解析が困難なため、矩形波における基本波(第1高調波)の伝達関数を求めています。

インピーダンス計算による伝達関数の導出

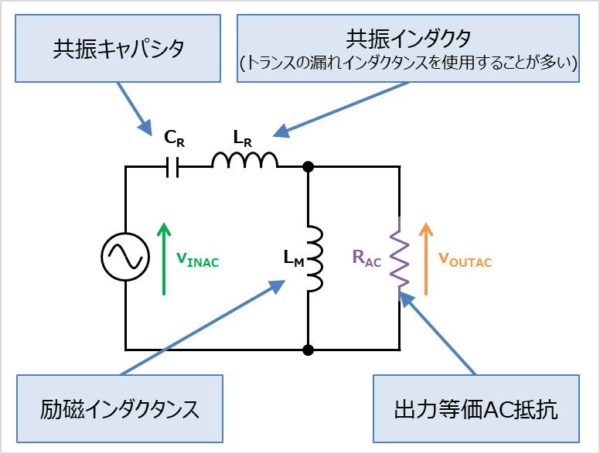
LLCコンバータの設計において、インピーダンス計算すると伝達関数\(M\)は以下の式で表されます。

\begin{eqnarray}
|M|=\frac{1}{\sqrt{\left(1+\displaystyle\frac{1}{S}-\displaystyle\frac{1}{S{{\omega}_N}^2}\right)^2+Q^2\left({\omega}_N -\displaystyle\frac{1}{{\omega}_N}\right)^2}}
\end{eqnarray}

では、これから上式の導出方法について説明します。

導出方法

共振キャパシタ\(C_R\)と共振インダクタ\(L_R\)の直列インピーダンス\(Z_S\)は以下の式で表されます。
\begin{eqnarray}
Z_S=\frac{1}{j{\omega}C_R}+j{\omega}L_R
\end{eqnarray}
また、励磁インダクタ\(L_M\)と出力等価AC抵抗RACの並列インピーダンス\(Z_P\)は以下の式で表されます。
\begin{eqnarray}
Z_P=\frac{1}{\displaystyle\frac{1}{j{\omega}L_M}+\displaystyle\frac{1}{R_{AC}}}=\frac{j{\omega}L_M R_{AC}}{j{\omega}L_M+R_{AC}}
\end{eqnarray}
従って、「入力AC電圧の基本波成分\(v_{INAC}\)」と「出力AC電圧の基本波成分\(v_{OUTAC}\)」の比率である伝達関数\(M\)は以下の式で表すことができます。
\begin{eqnarray}
M&=&\frac{v_{OUTAC}}{v_{INAC}}\\
&=&\frac{ Z_P }{Z_P+Z_S}\\
&=&\frac{1}{1+\displaystyle\frac{Z_S}{Z_P}}\\
&=&\frac{1}{1+\left(\displaystyle\frac{1}{j{\omega}L_M}+\displaystyle\frac{1}{R_{AC}}\right)×\left(\displaystyle \frac{1}{j{\omega}C_R}+j{\omega}L_R\right)}\\
&=&\frac{1}{1-\displaystyle\frac{1}{{\omega}^2L_M C_R }+\displaystyle\frac{L_R}{L_M}+\displaystyle\frac{1}{j{\omega} C_RR_{AC}}+\displaystyle\frac{j{\omega}L_R}{R_{AC}}}\\
&=&\frac{1}{\left(1+\displaystyle\frac{L_R}{L_M}-\displaystyle\frac{1}{{\omega}^2L_M C_R }\right)+j\left(\displaystyle\frac{{\omega}L_R}{R_{AC}}-\displaystyle\frac{1}{{\omega}C_RR_{AC}}\right)}
\end{eqnarray}

上式において、分母の実部と虚部を整理するために以下の4式を用います。

１．直列共振角周波数\({\omega}_R\)

共振キャパシタ\(C_R\)と共振インダクタ\(L_R\)の直列共振角周波数\({\omega}_R\)は、以下の式で表すことができます。
\begin{eqnarray}
{\omega}_R=\frac{1}{\sqrt{L_RC_R}}\tag{1}
\end{eqnarray}

正規化角周波数\({\omega}_N\)

正規化角周波数\({\omega}_N\)は任意の角周波数wを直列共振角周波数\({\omega}_N\)で正規化した式となり、以下の式で表すことができます。
\begin{eqnarray}
{\omega}_N=\frac{{\omega}}{{\omega}_R}\tag{2}
\end{eqnarray}

インダクタンス比率\(S\)

共振インダクタ\(L_R\)と励磁インダクタ\(L_M\)の比率をSと置くと、インダクタンス比率Sは以下の式で表すことができます。
\begin{eqnarray}
S=\frac{L_M}{L_R}\tag{3}
\end{eqnarray}

Q値

共振の鋭さを表すQ値は、出力等価AC抵抗\(R_{AC}\)と特性インピーダンス\(Z_O\)を用いると、以下の式で表すことができます。
\begin{eqnarray}
Q=\frac{Z_O}{R_{AC}}=\frac{\sqrt{\displaystyle\frac{L_R}{C_R}}}{R_{AC}}=\frac{{\omega}_RL_R}{R_{AC}}=\frac{1}{{\omega}_RC_RR_{AC}}\tag{4}
\end{eqnarray}

これら4式のうち、(1)～(3)式を用いると、分母の実部は以下のように整理することができます。
\begin{eqnarray}
&&1+\displaystyle\frac{L_R}{L_M}-\displaystyle\frac{1}{{\omega}^2L_M C_R }\\
&=&1+\displaystyle\frac{L_R}{L_M}-\displaystyle\frac{1}{{{\omega}_N }^2{{\omega}_R}^2SL_RC_R}\\
&=&1+\displaystyle\frac{L_R}{L_M}-\displaystyle\frac{1}{{{\omega}_N }^2{{\omega}_R}^2S\displaystyle\frac{1}{{{\omega}_R}^2}}\\
&=&1+\frac{1}{S}-\frac{1}{S{{\omega}_N}^2}
\end{eqnarray}

また、これら4式のうち、(1),(2),(4)式を用いると、分母の虚部は以下のように整理することができます。
\begin{eqnarray}
&&\displaystyle\frac{{\omega}L_R}{R_{AC}}-\displaystyle\frac{1}{{\omega}C_RR_{AC}}\\
&&=\displaystyle\frac{{\omega}_N{\omega}_RL_R}{R_{AC}}-\displaystyle\frac{1}{{\omega}_N{\omega}_R C_RR_{AC}}\\
&&={\omega}_NQ-\frac{Q}{{\omega}_N}\\
&&=Q\left({\omega}_N-\frac{1}{{\omega}_N}\right)
\end{eqnarray}

したがって、伝達関数\(M\)はインダクタンス比率S、正規化角周波数\({\omega}_N\)、Q値をパラメータとして用いると、以下の式で表すことができます。なお、伝達関数\(M\)の絶対値\(|M|\)がゲインとなります。

\begin{eqnarray}
M&=&\frac{1}{\left(1+\displaystyle\frac{1}{S}-\displaystyle\frac{1}{S{{\omega}_N}^2}\right)+j Q\left({\omega}_N-\displaystyle\frac{1}{{\omega}_N}\right)}\\
|M|&=&\frac{1}{\sqrt{\left(1+\displaystyle\frac{1}{S}-\displaystyle\frac{1}{S{{\omega}_N}^2}\right)^2+Q^2\left({\omega}_N -\displaystyle\frac{1}{{\omega}_N}\right)^2}}
\end{eqnarray}

補足

インダクタンス比率\(S\)の変数は「\(k\)」や「\(m\)」としている参考書やネット記事もあります。