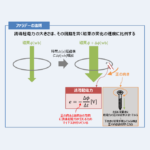
一様な磁束密度の中で導体棒が動くと、誘導起電力が発生します。
この誘導起電力の大きさ、向き、例題について図を用いて説明しています。
導体棒の誘導起電力
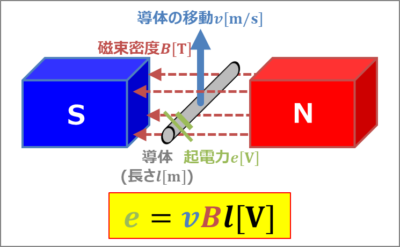
磁束密度\(B{\mathrm{[T]}}\)の磁界中を、長さ\(l{\mathrm{[m]}}\)の導体棒が速度\(v{\mathrm{[m/s]}}\)で磁界の方向に対して垂直に動くと、次式で表される誘導起電力\(e{\mathrm{[V]}}\)が発生します。
誘導起電力の大きさ
\begin{eqnarray}
e=vBl{\mathrm{[V]}}\tag{1}
\end{eqnarray}
これから上式の誘導起電力について『大きさの導出方法』と『向きの決め方』について説明します。
大きさの導出方法
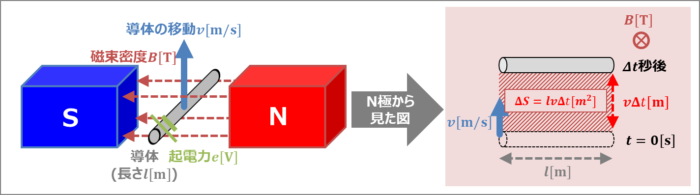
上図は磁束密度\(B{\mathrm{[T]}}\)の磁界中を、長さ\(l{\mathrm{[m]}}\)の導体棒が速度\(v{\mathrm{[m/s]}}\)で磁界の方向に対して垂直に動いている様子を表しています。
速度\(v{\mathrm{[m/s]}}\)で動いているということは、\({\Delta}t\)秒後には\(v{\Delta}t{\mathrm{[m]}}\)の距離を動いているということになります。
導体棒の長さは\(l{\mathrm{[m]}}\)なので、\({\Delta}t\)秒間移動することによって変化した面積\({\Delta}S{\mathrm{[m^2]}}\)は次式となります。
\begin{eqnarray}
{\Delta}S=l{\mathrm{[m]}}×v{\Delta}t{\mathrm{[m]}}=lv{\Delta}t{\mathrm{[m^2]}}\tag{2}
\end{eqnarray}
この変化した面積\({\Delta}S{\mathrm{[m^2]}}\)を1回巻きのコイル(\(N=1\))と見なすことがポイントとなります。
磁束密度\(B{\mathrm{[T]}}\)は変化しませんが、導体棒が磁界中を動くことで、面積\(S{\mathrm{[m^2]}}\)が変わるため、磁束鎖交数\({\psi}{\mathrm{[wb]}}\)が変化します。
『\({\Delta}t\)秒間での磁束鎖交数\({\psi}{\mathrm{[wb]}}\)の変化量\({\Delta}{\psi}{\mathrm{[wb]}}\)』は、『上図の変化した面積\({\Delta}S{\mathrm{[m^2]}}\)を通る磁束鎖交数\({\psi}{\mathrm{[wb]}}\)』と等しいため、次式で表すことができます。
\begin{eqnarray}
{\Delta}{\psi}=N{\Delta}{\phi}=N×B{\Delta}S=1×Blv{\Delta}t=Blv{\Delta}t{\mathrm{[wb]}}\tag{3}
\end{eqnarray}
なお、(3)式の\({\phi}\)は磁束を表しています。磁束\({\phi}{\mathrm{[wb]}}\)と磁束鎖交数\({\psi}{\mathrm{[wb]}}\)には『\({\psi}=N{\phi}\)』の関係があります。
したがって、ファラデーの法則を用いると、導体棒に発生する誘導起電力\(e{\mathrm{[V]}}\)は次式となります。
\begin{eqnarray}
e=\left|-\frac{{\Delta}{\psi}}{{\Delta}t}\right|=\left|-\frac{Blv{\Delta}t}{{\Delta}t}\right|=vBl{\mathrm{[V]}}\tag{4}
\end{eqnarray}
つまり、磁束密度\(B{\mathrm{[T]}}\)の磁界中を、長さ\(l{\mathrm{[m]}}\)の導体棒が速度\(v{\mathrm{[m/s]}}\)で磁界の方向に対して垂直に動いている場合に発生する誘導起電力は『\(e=vBl{\mathrm{[V]}}\)』になります。
上式で求めた『\(e=vBl{\mathrm{[V]}}\)』は、教科書やネットでは公式のように扱われていることが多いので、暗記することをオススメします。私は『\(e=vBl\)(ビビる)』と覚えていました。
ファラデーの法則とは
ファラデーの法則とは、「電磁誘導によって生じる誘導起電力の大きさは、その回路を貫く磁束の変化の速度に比例する」ことを表した法則です。詳しくは以下の記事に説明していますので、参考にしてください。
-

【ファラデーの法則とは?】『公式』や『積分形』や『微分形』などを詳しく解説!
続きを見る
向きの決め方
誘導起電力の向きは『フレミングの右手の法則』か『レンツの法則』によって求めることができます。
この記事では各々の法則を用いて誘導起電力の向きを求めていますので、お好きなで理解してくださいね。
フレミングの右手の法則


まず、上図に示すように、右手の親指、人差し指、中指が直角になるようにします。
各指は以下の方向を表しています。
フレミングの右手の法則
- 親指:導体棒が磁力線を横切る方向
人差し指:磁力線の方向(磁束密度の方向)
中指:導体が移動することによって発生する誘導起電力の方向
今回は、導体棒が磁力線を横切る方向と磁束密度の方向が分かっているため、誘導起電力の向きを求めます。
導体の移動方向を親指に、磁束密度の方向を中指にすると、誘導起電力の向きは中指の方向(裏から表の方向)になります。
レンツの法則

誘導起電力の向きはレンツの法則によって求めることができます。
レンツの法則とは、「電磁誘導によって生じる誘導起電力の向き」を表した法則です。誘導起電力の向きは「元の磁束の変化を妨げる方向」となります。
レンツの法則について詳しくは以下の記事に説明していますので、参考にしてください。
-


【レンツの法則とは】起電力の向きについてわかりやすく解説!
続きを見る
まず、導体棒の上側と下側のどちらかに仮想の空間を考えます。
導体棒の上側に仮想の空間を考えた場合
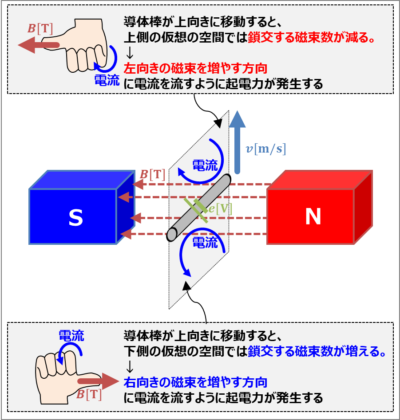
導体棒が上向きに移動すると、導体棒の上側の仮想の空間では鎖交する磁束数が減ります。
それを打ち消すため、左向きの磁束を増やす方向に電流を流すように誘導起電力が発生します。その向きは右ねじの法則によって求めます。
導体棒の下側に仮想の空間を考えた場合
導体棒が上向きに移動すると、導体棒の下側の仮想の空間では鎖交する磁束数が増えます。
それを打ち消すため、左向きの磁束を減らす方向(すなわち、右向きの磁束を増やす方向)に電流を流すように誘導起電力が発生します。その向きは右ねじの法則によって求めます。
上側と下側どちらの領域でも誘導起電力の向きは裏から表の方向になることがわかります。
導体棒が斜めに移動した時の誘導起電力
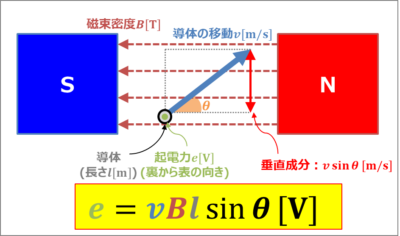

上図に示すように、磁束密度\(B{\mathrm{[T]}}\)の磁界中を、長さ\(l{\mathrm{[m]}}\)の導体棒が速度\(v{\mathrm{[m/s]}}\)で磁界の方向に対して、角度\({\theta}\)で動いている場合に発生する誘導起電力\(e{\mathrm{[V]}}\)は次式となります。
誘導起電力の大きさ
\begin{eqnarray}
e=vBl{\sin}{\theta}{\mathrm{[V]}}\tag{5}
\end{eqnarray}
導体棒は斜めに移動していますが、磁界に対して垂直に移動している成分は\(v{\sin}{\theta}{\mathrm{[m/s]}}\)となります。そのため、(1)式の『\(v\)』が『\(v{\sin}{\theta}\)』に変わるのです。
上式において、磁界と平行に導体棒が移動すれば、『\({\sin}0°=0\)』なので、誘導起電力\(e{\mathrm{[V]}}\)は0Vとなります。また、磁界と垂直に導体棒が移動すれば、『\({\sin}90°=1\)』となり、(5)式は(1)式と同じになります。
導体棒の誘導起電力に関する例題
例題1
まずは以下の簡単な例題から解いてみましょう。
例題1
下図に示すように、磁束密度\(B=0.2{\mathrm{[T]}}\)の磁界中を長さ\(l=0.1{\mathrm{[m]}}\)の導体棒が磁界に対して\({\theta}=45°\)の方向に速度\(v=10{\mathrm{[m/s]}}\)で動いている時、導体の両端に発生する誘導起電力\(e{\mathrm{[V]}}\)は何ボルトか求めてみましょう。
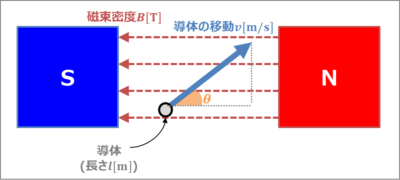

解答
(5)式を用いると、誘導起電力\(e{\mathrm{[V]}}\)は以下の値となります。
\begin{eqnarray}
e&=&vBl{\sin}{\theta}\\
&=&10×0.2×1×{\sin}45°\\
&{\approx}&1.41{\mathrm{[V]}}\tag{1-1}
\end{eqnarray}
例題2
例題2
幅\(l{\mathrm{[m]}}\)、質量\(m{\mathrm{[kg]}}\)、抵抗\(R{\mathrm{[Ω]}}\)の導体棒abを水平にかけて閉回路を作る。この閉回路に対して、垂直に磁束密度\(B{\mathrm{[T]}}\)の磁界をかけ、導体棒abを自由落下させる。なお、終速度を\(v{\mathrm{[m/s]}}\)とする。
- (1)導体棒abに発生する誘導起電力\(e{\mathrm{[V]}}\)の大きさを求めてみましょう。
- (2)誘導起電力\(e{\mathrm{[V]}}\)は導体棒のaとbではどちらが高電位でしょうか。
- (3)時間\(t{\mathrm{[s]}}\)の間に抵抗\(R{\mathrm{[Ω]}}\)で発生するジュール熱\(Q{\mathrm{[J]}}\)はいくらでしょうか。
- (4)導体棒abが磁場から受ける電磁力\(F{\mathrm{[N]}}\)はいくらはでしょうか。
- (5)電磁力\(F{\mathrm{[N]}}\)の向きはどちらでしょうか。
- (6)導体棒の終速度\(v{\mathrm{[m/s]}}\)はいくらでしょうか。
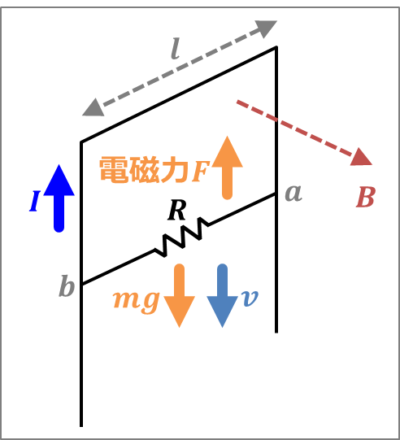

解答
(1)導体棒abに発生する誘導起電力\(e{\mathrm{[V]}}\)の大きさを求めてみましょう。
(1)式を用います。誘導起電力\(e{\mathrm{[V]}}\)は、幅\(l{\mathrm{[m]}}\)、磁束密度\(B{\mathrm{[T]}}\)、終速度\(v{\mathrm{[m/s]}}\)なので次式となります。
\begin{eqnarray}
e=vBl{\mathrm{[V]}}\tag{2-1}
\end{eqnarray}
(2)誘導起電力\(e{\mathrm{[V]}}\)は導体棒のaとbではどちらが高電位でしょうか。
レンツの法則を用います。
導体棒abは自由落下しているため、閉回路を貫く鎖交する磁束数が増えます。
それを打ち消すため、磁束を減らす方向に電流を流すように誘導起電力が発生します。その向きは右ねじの法則を用いると、高電位の箇所は『b』となります。
(3)時間\(t{\mathrm{[s]}}\)の間に抵抗\(R{\mathrm{[Ω]}}\)で発生するジュール熱\(Q{\mathrm{[J]}}\)はいくらでしょうか。
抵抗\(R{\mathrm{[Ω]}}\)には誘導起電力\(e=vBl{\mathrm{[V]}}\)が印加されているため、抵抗\(R{\mathrm{[Ω]}}\)での電力\(P{\mathrm{[W]}}\)は次式となります。
\begin{eqnarray}
P=\frac{e^2}{R}=\frac{v^2B^2l^2}{R}{\mathrm{[W]}}\tag{2-2}
\end{eqnarray}
この電力\(P{\mathrm{[W]}}\)が時間\(t{\mathrm{[s]}}\)の間印加されているため、ジュール熱\(Q{\mathrm{[J]}}\)は次式となります。
\begin{eqnarray}
Q=Pt=\frac{v^2B^2l^2}{R}t{\mathrm{[J]}}\tag{2-3}
\end{eqnarray}
(4)導体棒abが磁場から受ける電磁力\(F{\mathrm{[N]}}\)はいくらはでしょうか。
導体棒を流れる電流\(I{\mathrm{[A]}}\)はオームの法則より求めることができます。
誘導起電力\(e=vBl{\mathrm{[V]}}\)と抵抗\(R{\mathrm{[Ω]}}\)より、電流\(I{\mathrm{[A]}}\)は次式となります。
\begin{eqnarray}
I=\frac{e}{R}=\frac{vBl}{R}{\mathrm{[A]}}\tag{2-4}
\end{eqnarray}
この電流\(I{\mathrm{[A]}}\)が流れることにより、磁場から電磁力\(F{\mathrm{[N]}}\)を受けます。この電磁力\(F{\mathrm{[N]}}\)は次式となります。
\begin{eqnarray}
F=IBl=\frac{vBl}{R}×Bl=\frac{vB^2l^2}{R}{\mathrm{[N]}}\tag{2-5}
\end{eqnarray}
(5)電磁力\(F{\mathrm{[N]}}\)の向きはどちらでしょうか。
電磁力\(F{\mathrm{[N]}}\)の向きはフレミングの左手の法則により上向きとなります。
左手の親指、人差し指、中指が直角になるようにして、人差し指を磁束密度の方向、中指を導体棒に流れている電流の方向に向けた時、親指の方向が導体棒が受ける力の方向となります。
フレミングの左手の法則
- 親指:導体棒が受ける力の方向
人差し指:磁力線の方向(磁束密度の方向)
中指:導体棒に流れている電流の方向
(6)導体棒の終速度\(v{\mathrm{[m/s]}}\)はいくらでしょうか。
電磁力\(F{\mathrm{[N]}}\)と重力\(mg{\mathrm{[N]}}\)がつり合うとき、速度が一定となります。そのため、終速度\(v{\mathrm{[m/s]}}\)は次式となります。
\begin{eqnarray}
F&=&mg\\
\frac{vB^2l^2}{R}&=&mg\\
{\Leftrightarrow}v&=&\frac{mgR}{B^2l^2}{\mathrm{[m/s]}}\tag{2-6}
\end{eqnarray}
まとめ
この記事では導体棒の誘導起電力について、以下の内容を説明しました。
当記事のまとめ
- 導体棒が動く時に発生する誘導起電力の『大きさ』と『向き』
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。