【ファラデーの法則とは？】『公式』や『積分形』や『微分形』などを詳しく解説！

この記事ではファラデーの法則について

ファラデーの法則とは
『ファラデーの法則』の公式
『ファラデーの法則』の積分形と微分形
『ファラデーの法則』に関する問題

などを図を用いて分かりやすく説明しています。

ファラデーの法則とは

ファラデーの法則とは、「電磁誘導によって生じる誘導起電力の大きさは、その回路を貫く磁束の変化の速度に比例する」ことを表した法則です。英語では、「Faraday's law」と書きます。ファラデーの法則は1831年にイギリスの物理学者マイケル・ファラデーによって発見されました。

ではこれからこのファラデーの法則の公式、微分形、積分形を順番に説明していきます。

『ファラデーの法則』と『レンツの法則』

ファラデーの法則は誘導起電力の「大きさ」を表します。一方、レンツの法則は誘導起電力の「向き」を表します。

ファラデーの法則の公式

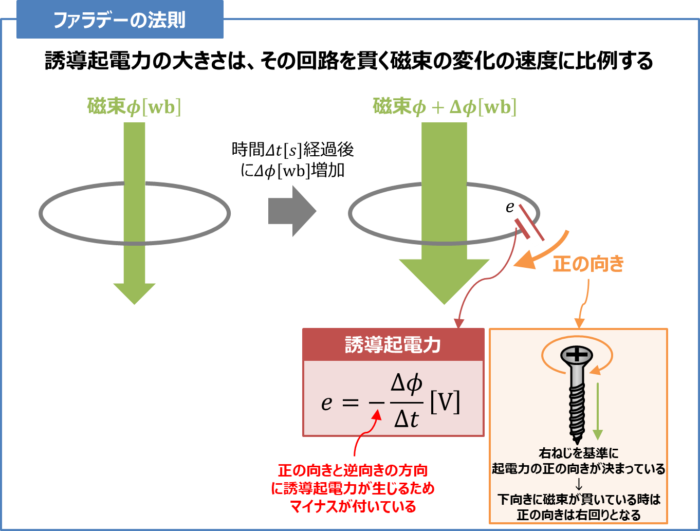
上図に示すように、1回巻きのコイルを貫く磁束\({\phi}{\mathrm{[wb]}}\)が\({\Delta}t{\mathrm{[s]}}\)の間に\({\Delta}{\phi}{\mathrm{[wb]}}\)変化すると、そのコイルには次式の誘導起電力\(e{\mathrm{[V]}}\)が生じます。

\begin{eqnarray}
e=-\frac{{\Delta}{\phi}}{{\Delta}t}{\mathrm{[V]}}\tag{1}
\end{eqnarray}

なお、コイルの巻数が\(N\)のときは、コイルには次式の誘導起電力\(e{\mathrm{[V]}}\)が生じます。

\begin{eqnarray}
e=-N\frac{{\Delta}{\phi}}{{\Delta}t}{\mathrm{[V]}}\tag{2}
\end{eqnarray}

なお、磁束鎖交数\({\psi}{\mathrm{[wb]}}\)は「磁束鎖交数\({\psi}\)=巻数\(N\)×磁束\({\phi}\)」の関係があるため、(2)式は次式に変形することができます。

\begin{eqnarray}
e=-N\frac{{\Delta}{\phi}}{{\Delta}t}=-\frac{{\Delta}{\psi}}{{\Delta}t}{\mathrm{[V]}}\tag{3}
\end{eqnarray}

なお、「数学の微分\(d\)」を使って表している場合もあります。この場合、(3)式は次式となります。

\begin{eqnarray}
e=-N\frac{d{\phi}}{dt}=-\frac{d{\psi}}{dt}{\mathrm{[V]}}\tag{4}
\end{eqnarray}

(3)式or(4)式が電磁誘導に関するファラデーの法則の公式です。

マイナスが付く理由

(1)式にあるマイナスはレンツの法則により、「磁束\({\phi}\)の変化の"妨げる"」という意味で付けられています。

誘導起電力は右ねじを基準に決められています。そのため、例えば、下向きに磁束\({\phi}\)が貫いているときには、正の向きは右回りとなります。

ここで、下向きの磁束\({\phi}\)が増えた場合、レンツの法則より、磁束の変化を妨げる方向に誘導起電力が生じます。すなわち、上向きの磁束をつくるような誘導起電力が生じます。この誘導起電力の向きは左回りとなります。これは負の向きなので式にマイナスが付きます。

ファラデーの法則の積分形

上図に示すように、1回巻きのコイルを貫く磁束\({\phi}{\mathrm{[wb]}}\)が変化するとき、このコイルの誘導起電力\(e{\mathrm{[V]}}\)をコイルに沿う電界の強さ\({\vec{E}}\)を用いて表すと、次式のような周回積分の形で表すことができます。

\begin{eqnarray}
e={\displaystyle\oint}_{{\partial}S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{l}}=-\frac{d{\psi}}{dt}=-1{\;}{\cdot}{\;}\frac{d{\phi}}{dt}{\mathrm{[V]}}\tag{5}
\end{eqnarray}

また、コイルの面において、微小面積\(d{\vec{S}}\)をとり、その場所における磁束密度を\({\vec{B}}{\mathrm{[T]}}\)とすると、「磁束鎖交数\({\psi}\)(=巻数\(1\)×磁束\({\phi}\))」は「\({\vec{B}}{\;}{\cdot}{\;}d{\vec{S}}\)をコイルの全面積\(S\)について面積積分したもの」に等しいため、次式が成り立ちます。

\begin{eqnarray}
{\psi}={\phi}={\displaystyle\int}_{S}{\vec{B}}{\;}{\cdot}{\;}d{\vec{S}}{\mathrm{[wb]}}\tag{6}
\end{eqnarray}

(6)式を(5)式に代入すると、ファラデーの法則の積分形を導出することができます。

ファラデーの法則の積分形

\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{l}}=-\frac{d}{dt}{\displaystyle\int}_{S}{\vec{B}}{\;}{\cdot}{\;}d{\vec{S}}{\mathrm{[V]}}\tag{7}
\end{eqnarray}

上式は「面の境界\({{\partial}S}\)において、電界の接線\({\vec{E}}\)を足し合わせる(積分する)と、足し合わせた結果は、磁束密度\({\vec{B}}\)の時間微分の面積分の和に等しくなる」ということを表しています。

ファラデーの法則の微分形

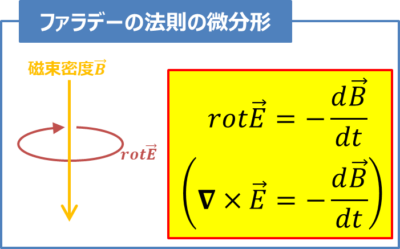
ファラデーの法則の積分形にストークスの定理を用いると、微分形を導出することができます。

ストークスの定理とは、「回転\(rot{\vec{A}}\)を面\(S\)で面積分したものは、接線\({\vec{A}}\)を面の境界\({{\partial}S}\)で線積分したものと等しくなる」というもので以下の式で表されます。

\begin{eqnarray}
\displaystyle\int_{S}{rot{\vec{A}}}{\;}{\cdot}{\;}d{\vec{S}}=\displaystyle\int_{{\partial}S}{\vec{A}}{\;}{\cdot}{\;}d{\vec{l}}\tag{8}
\end{eqnarray}

これを、ファラデーの法則の積分形に当てはめてみましょう。

(7)式のファラデーの法則の積分形の左辺にストークスの定理を当てはめると、次式となります。

\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{l}}=\displaystyle\int_{S}{rot{\vec{E}}}{\;}{\cdot}{\;}d{\vec{S}}\tag{9}
\end{eqnarray}

(9)式を(7)式に代入すると次式となります。

\begin{eqnarray}
\displaystyle\int_{S}{rot{\vec{E}}}{\;}{\cdot}{\;}d{\vec{S}}=-\frac{d}{dt}{\displaystyle\int}_{S}{\vec{B}}{\;}{\cdot}{\;}d{\vec{S}}\tag{10}
\end{eqnarray}

(10)式から面積分を取ると、ファラデーの法則の微分形を導出することができます。

ファラデーの法則の微分形

\begin{eqnarray}
{rot{\vec{E}}}=-\frac{d{\vec{B}}}{dt}\tag{11}
\end{eqnarray}

上式は「磁束密度\({\vec{B}}\)が変化すると、電界\({\vec{E}}\)の回転が生じる」ということを表しています。