【ガウスの法則とは】『公式』や『積分形』や『微分形』などを解説！

この記事では『ガウスの法則』について

ガウスの法則とは？
ガウスの法則の導出方法
ガウスの法則の公式
ガウスの法則の積分形
ガウスの法則の微分形

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

ガウスの法則とは

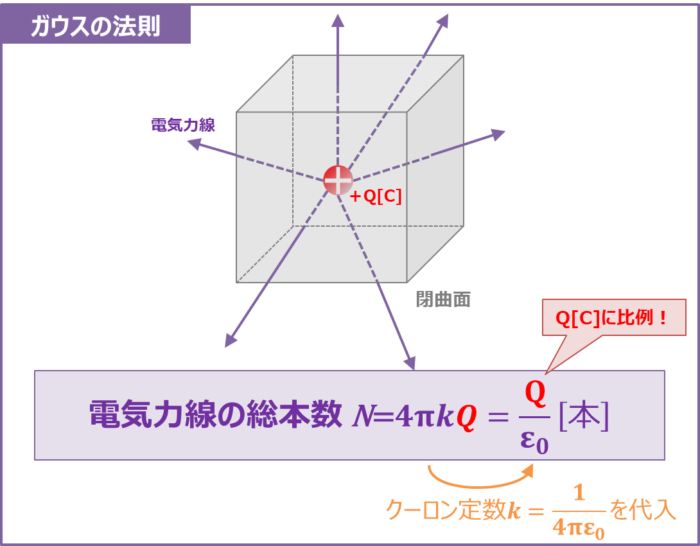
ガウスの法則とは、ある閉曲面(上図では立方体)を貫く電気力線の総本数N[本]は、閉曲面内部に存在する電荷の電気量をQ[C]とすると、

\begin{eqnarray}
N=4{\pi}kQ=\frac{Q}{{\varepsilon}_0}{\mathrm{[本]}}
\end{eqnarray}

になるという法則です。

このガウスの法則は何が言いたいのかというと、

閉曲面を貫く電気力線の総本数N[本]は閉曲面内部に存在する電荷の電気量Q[C]に比例するよ！

ということです。

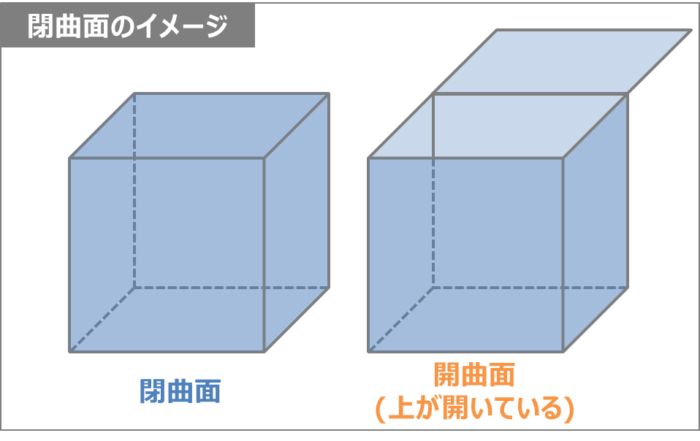
ここで閉曲面とは完全に閉鎖された立体のことを指します。例えば、下図の場合、左側の図形は閉鎖されているので閉曲面となりますが、右側の図形は上が開いているため、閉曲面とはなりません。

では、次に電気力線の総本数N[本]が\({\lceil}N=4{\pi}kQ=\displaystyle\frac{Q}{{\varepsilon}_0}{\mathrm{[本]}}{\rfloor}\)となる理由について説明してきます。

ガウスの法則の導出

まず『電気力線の本数と向きの定義』から・・・

ある閉曲面を貫く電気力線の総本数N[本]を求めるためにはまず『電気力線の本数と向きの定義』について理解する必要があります。

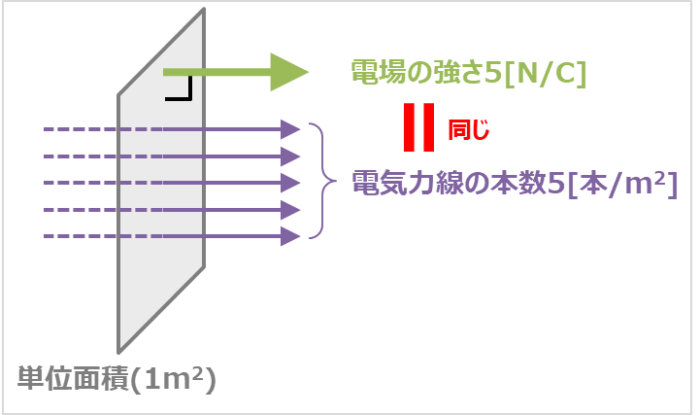
上図に単位面積(1m²)の平面とその平面を垂直に貫く電場を示しています。ここで、電場の強さはE[N/C]とします。

では、この平面を貫く電気力線の本数は何本でしょうか？

『電気力線の本数と向きの定義は以下のように決められています。

電気力線の本数と向きの定義

単位面積(1m²)の平面を貫く電気力線の本数は電場の強さE[N/C]と同じである。
電気力線の方向は電場と同じである。

そのため、上図においては、単位面積(1m²)の平面を貫く電気力線の本数はE[本/m²]となり、平面に対して垂直に電気力線が貫いていることになります。

例えば、下図の場合、電場の強さEが5[N/C]となっています。そのため、「単位面積(1m²)の平面に電気力線は5[本/m²]貫いている」ということになります。

電気力線とは、このように電場(電界)の様子を仮想的な線で表したものです。電気力線については以下の記事で詳しく説明していますので、参考にしていただければ幸いです。

球を貫く電気力線の総本数

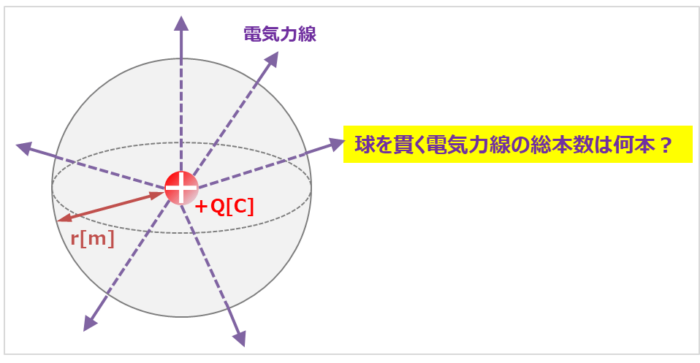
次に一例として、上図に示すように、半径rの球があり、その球の中心に点電荷Qがある場合を考えてみましょう。

この時、球を貫く電気力線の総本数は何本でしょうか？

また、上図から分かると思いますが、点電荷Qから出る電気力線は、そのまま球を貫きます。そのため、球を貫く電気力線の総本数が分かれば、点電荷Qから出る電気力線の総本数が分かるということになります。

では、球を貫く電気力線の本数を求めてみましょう。

球を貫く電気力線の本数の求め方

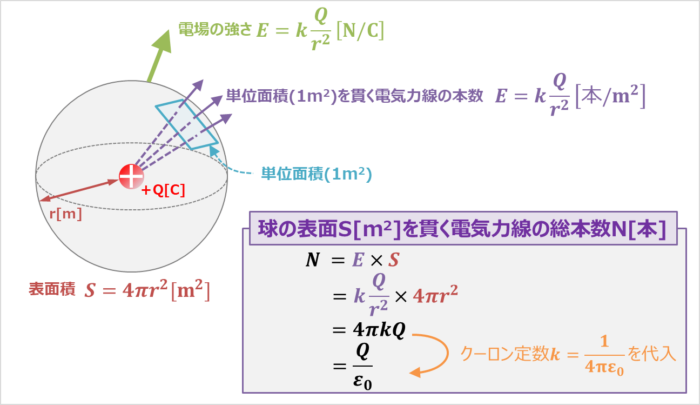
点電荷Qから距離rの位置における電場の強さはE[N/C]は

\begin{eqnarray}
E=k\frac{Q}{r^2}{\mathrm{[N/C]}}
\end{eqnarray}

となります。

ここで、『電気力線の本数と向きの定義』より、球の表面の単位面積(1m²)を貫く電気力線の本数は電場の強さE[N/C]と同じであるため、

\begin{eqnarray}
球の表面の単位面積(1{\mathrm{m^2}})を貫く電気力線の本数&=&E\\
&=&k\frac{Q}{r^2}{\mathrm{[本/m^2]}}
\end{eqnarray}

となります。また、半径rの球の表面積S[m²]は

\begin{eqnarray}
S=4{\pi}r^2{\mathrm{[m^2]}}
\end{eqnarray}

となります。すなわち、球の表面S[m²]を貫く電気力線の総本数N[本](すなわち、点電荷Qから出る電気力線の総本数N[本])は、

\begin{eqnarray}
N&=&E×S\\
&=&k\frac{Q}{r^2}{\mathrm{[本/m^2]}}×4{\pi}r^2{\mathrm{[m^2]}}\\
&=&4{\pi}kQ{\mathrm{[本]}}
\end{eqnarray}

となります。ここで、上式にあるkはクーロン定数と呼ばれるものであり、

\begin{eqnarray}
k=\frac{1}{4{\pi}{\varepsilon}_{0}}
\end{eqnarray}

と表されます。したがって、球の表面S[m²]を貫く電気力線の総本数N[本]は、

\begin{eqnarray}
N&=&4{\pi}kQ\\
&=&4{\pi}×\frac{1}{4{\pi}{\varepsilon}_{0}}×Q\\
&=&\frac{Q}{{\varepsilon}_{0}}{\mathrm{[本]}}
\end{eqnarray}
となるのです。

ここでガウスの法則を復習してみましょう。ガウスの法則とは、ある閉曲面を貫く電気力線の総本数N[本]は、閉曲面内部に存在する電荷の電気量をQ[C]とすると、

\begin{eqnarray}
N=4{\pi}kQ=\frac{Q}{{\varepsilon}_0}{\mathrm{[本]}}
\end{eqnarray}

になるという法則です。

このガウスの法則を導出するために、この記事では

ある閉曲面→半径rの球
閉曲面内部に存在する電荷→半径rの球の中心にある電気量がQの点電荷

として考えました。あくまで式の導出のために、半径rの球の中心に点電荷Qがあると考えているのです。

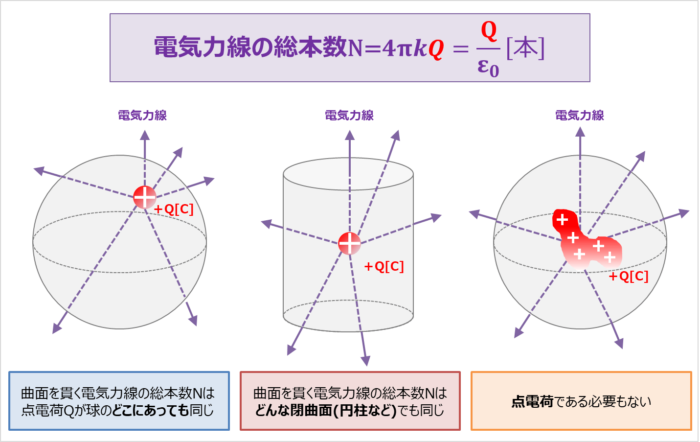
そのため、閉曲面を貫く電気力線の総本数N[本]は下図のように、電荷の位置、閉曲面の形、電荷の形によらずN=4πkQ[本]となります。

点電荷Qが球の内部のどこにあっても同じ。
球ではなくどんな閉曲面(例えば、円柱など)でも同じ。
点電荷である必要もない。

ガウスの法則の公式

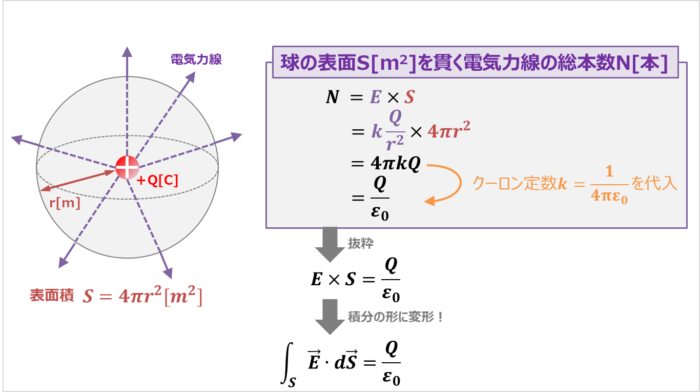
半径rの球の中心に点電荷Qがある場合、半径rの球の表面S[m²]を垂直に貫く電気力線の総本数N[本]は、

\begin{eqnarray}
N=E×S=4{\pi}kQ=\frac{Q}{{\varepsilon}_0}{\mathrm{[本]}}
\end{eqnarray}

になることを説明しました。

上式の一部を抜粋すると、

\begin{eqnarray}
E×S=\frac{Q}{{\varepsilon}_0}
\end{eqnarray}

となります。この左辺を積分の形にしたものがガウスの法則の公式となり次式となります。

ガウスの法則の公式

\begin{eqnarray}
\displaystyle\int_S {\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=\frac{Q}{{\varepsilon}_0}
\end{eqnarray}

上式の左辺の意味

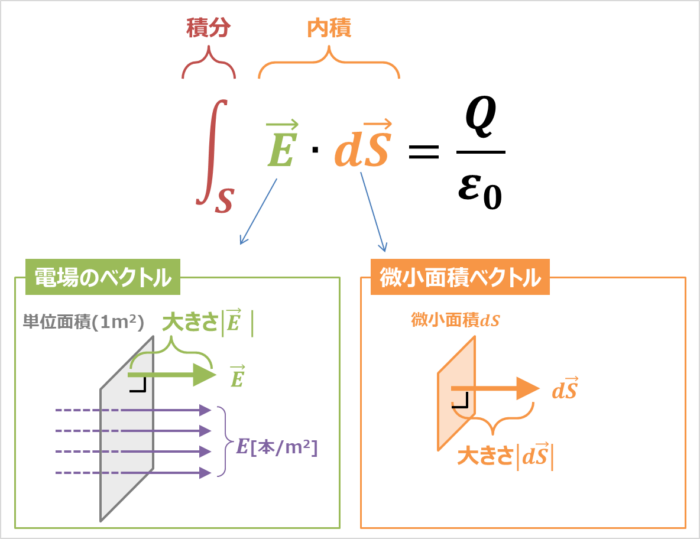
左辺は任意の閉曲面を垂直に貫く電気力線の総本数を示しています。

『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』は電場のベクトル\({\vec{E}}\)と微小面積ベクトル\(d{\vec{S}}\)の内積であり、その内積を積分(=面積分)しています。

電場のベクトル\({\vec{E}}\)

電場には向きがあるので、それをベクトルで表しているだけです。『電場のベクトル\({\vec{E}}\)の大きさ\(|{\vec{E}}|\)』は電場の強さE[N/C]と等しくなります。そのため、電場のベクトル\({\vec{E}}\)を用いる場合、単位面積(1m²)の平面を垂直に貫く電気力線の本数は『電場のベクトル\({\vec{E}}\)の大きさ\(|{\vec{E}}|\)』となります。

微小面積ベクトル\(d{\vec{S}}\)

面には向きがあるので、それをベクトルで表しているだけです。ベクトルの向きは面に垂直な方向(法線方向)で、『微小面積ベクトル\(d{\vec{S}}\)の大きさ\(|d{\vec{S}}|\)』は微小面積dSと等しくなります。

積分する理由

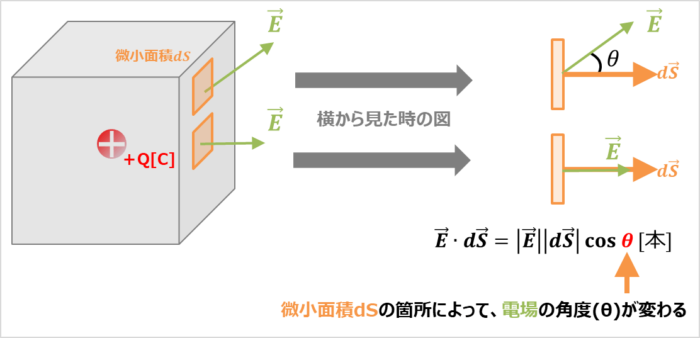
ここで、内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を積分している理由ですが、それは、任意の閉曲面(例えば、立方体など)の場合だと、面に対して常に電場 (電気力線)が同じ角度で貫いているとは限らないからです。

内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』は『電場のベクトル\({\vec{E}}\)の大きさ\(|{\vec{E}}|\)』と『微小面積ベクトル\(d{\vec{S}}\)の大きさ\(|d{\vec{S}}|\)』を用いると次式となります。

\begin{eqnarray}
{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=|{\vec{E}}||d{\vec{S}}|{\cos{{\theta}}}
\end{eqnarray}

そのため、任意の閉曲面を微小面積dSに分割したとき、微小面積dSの箇所によって、貫く電場の角度(\({\theta}\))が変わると、内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』の値が変わります。したがって、各々の微小面積dSにおける内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を足し合わせる(=面積分)する必要があるのです。

つまり、言い換えると、面積分は以下の条件では必要なくなります。

面積分をしなくていい条件

各々の微小面積dSによって貫く電場の角度(\({\theta}\))が同じの場合、各々の微小面積dSにおける内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を足し合わせる(=面積分)する必要がない

内積を考える理由

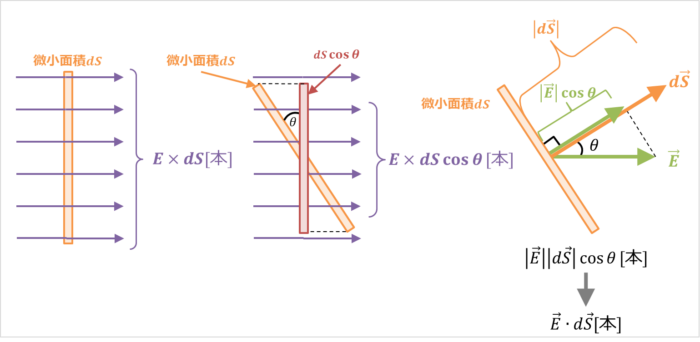
ここで、内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を考える理由ですが、それは、任意の閉曲面(例えば、立方体など)の場合だと、面に対して常に電場 (電気力線)が垂直に貫いているとは限らないからです。

例えば、下図の場合を考えてみましょう。

左側の図

微小面積dSと電気力線の向きが垂直のため、微小面積dSを貫く電気力線の本数は『\(E×dS\)』となります。

真ん中の図

微小面積dSと電気力線の向きを垂直に合わせる必要があります。電気力線が通過する実質的な面積は『\(dS{\cos{{\theta}}}\)』となります。そのため、微小面積dSを貫く電気力線の本数は『\(E×dS{\cos{{\theta}}}\)』となります。

右側の図

単位面積(1m²)の平面を貫く電気力線を電場のベクトル\({\vec{E}}\)で表したものとなっています。

微小面積dSと電場のベクトル\({\vec{E}}\)の向きを垂直に合わせると、微小面積dSを貫く電場のベクトル\({\vec{E}}\)の垂直成分は『\(|{\vec{E}}|{\cos{{\theta}}}\)』となります。したがって、微小面積dSを垂直に貫く電気力線の本数は『\(|{\vec{E}}||d{\vec{S}}|{\cos{{\theta}}}\)』となります。また、内積の公式より

\begin{eqnarray}
|{\vec{E}}||d{\vec{S}}|{\cos{{\theta}}}={\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}
\end{eqnarray}

となります。すなわち、内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』考えることで、微小面積dSを垂直に貫く電気力線の本数が分かるのです。

また、微小面積dSと電場の向きが垂直の場合(\({\theta}\)がゼロの場合)、\({\cos{\theta}}=1\)となるため、微小面積dSを垂直に貫く電気力線の本数は

\begin{eqnarray}
|{\vec{E}}||d{\vec{S}}|={\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}
\end{eqnarray}

となり、ただの掛け算となります。

つまり、内積は以下の条件では必要なくなります。

内積をしなくていい条件

微小面積dSと電場の向きが垂直の場合、内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を考える必要がなくなり、ただの掛け算で良い。

半径rの球の中心に点電荷Qがある場合

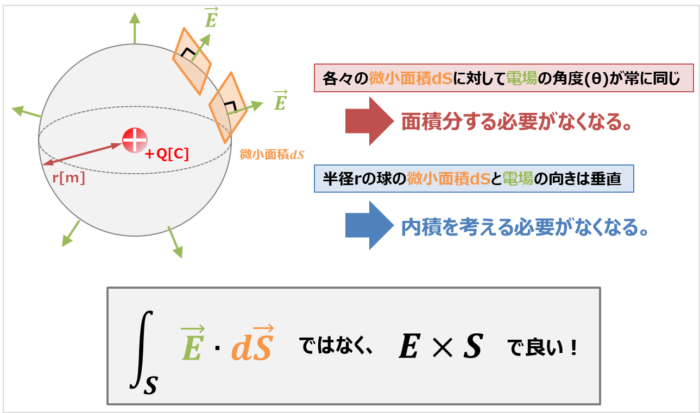
ここで、半径rの球の中心に点電荷Qがある場合をもう一度考えてみましょう。

面積分をしなくていい条件と、内積をしなくていい条件が当てはまることが分かります。

面積分をしなくていい条件

各々の微小面積dSによって貫く電場の角度(\({\theta}\))が同じの場合、各々の微小面積dSにおける内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を足し合わせる(=面積分)する必要がない

→半径rの球の微小面積dSの箇所によって、貫く電場の角度(\({\theta}\))が変わらず、常に垂直となります。そのため、各々の微小面積dSにおける内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を足し合わせる(=面積分)する必要がなくなります。

内積をしなくていい条件

微小面積dSと電場の向きが垂直の場合、内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』を考える必要がなくなり、ただの掛け算で良い。

→半径rの球の微小面積dSと電場の向きは垂直となります。そのため、内積『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』考える必要がなくなり、面積Sと電場Eの掛け算を良い。

したがって、半径rの球の中心に点電荷Qがある場合において、半径rの球を貫く電気力線の総本数Nを求める時には、面積分も内積もする必要がなく、単位面積(1m²)の平面を貫く電気力線の本数E[本/m²](すなわち、電場E)と半径rの球の表面積S[m²]の掛け算で良いため、『E×S』となるのです。

補足

ガウスの法則の公式は次式となりますが、以下のようの法線ベクトル\({\vec{n}}\)や\({\vec{E_n}}\)ベクトルを用いる場合があります。これらはすべて書き方が違うだけで同じものです。

ガウスの法則の公式

\begin{eqnarray}
\displaystyle\int_S {\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=\frac{Q}{{\varepsilon}_0}
\end{eqnarray}

法線ベクトル\({\vec{n}}\)を用いる場合(\(d{\vec{S}}={\vec{n}}dS\))

\begin{eqnarray}
\displaystyle\int_S {\vec{E}}{\;}{\cdot}{\;}{\vec{n}}dS=\frac{Q}{{\varepsilon}_0}
\end{eqnarray}

\({\vec{E_n}}\)ベクトルを用いる場合(\({\vec{E}}{\;}{\cdot}{\;}{\vec{n}}={\vec{E_n}}\))

\begin{eqnarray}
\displaystyle\int_S {\vec{E_n}}{\;}dS=\frac{Q}{{\varepsilon}_0}
\end{eqnarray}

ガウスの法則の積分形

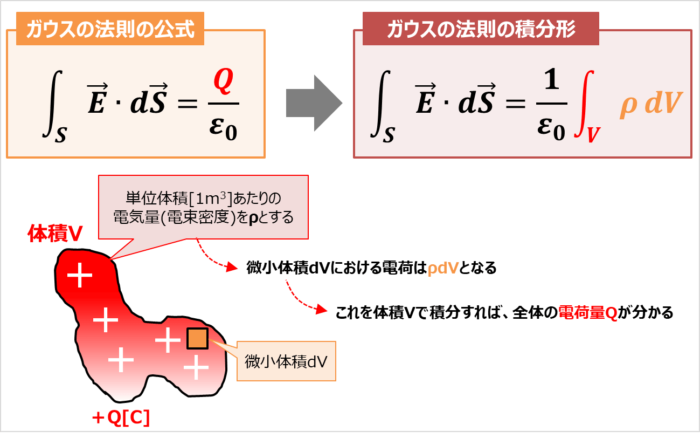
ガウスの法則の公式は次式となっています。

ガウスの法則の公式

\begin{eqnarray}
\displaystyle\int_S {\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=\frac{Q}{{\varepsilon}_0}
\end{eqnarray}

上式において、右辺を積分形に変形したものが「ガウスの法則の積分形」となります。

ガウスの法則の積分形

\begin{eqnarray}
\displaystyle\int_S {\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=\frac{1}{{\varepsilon}_0}\displaystyle\int_V {\rho}dV
\end{eqnarray}

右辺の意味

点電荷Qではなく、体積Vの大きさの帯電体を考えます。

体積Vの大きさの帯電体の単位体積(1m³)あたりの電気量(電荷密度)を\({\rho}\)とすると、電荷量Q[C]は

\begin{eqnarray}
Q=\displaystyle\int_V {\rho}dV{\mathrm{[C]}}
\end{eqnarray}

となります。

これを、ガウスの法則の公式に代入すると、

\begin{eqnarray}
\displaystyle\int_S {\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}&=&\frac{Q}{{\varepsilon}_0}\\
&=&\frac{1}{{\varepsilon}_0}\displaystyle\int_V {\rho}dV
\end{eqnarray}

となり、「ガウスの法則の積分形」の式となります。

ガウスの法則の微分形

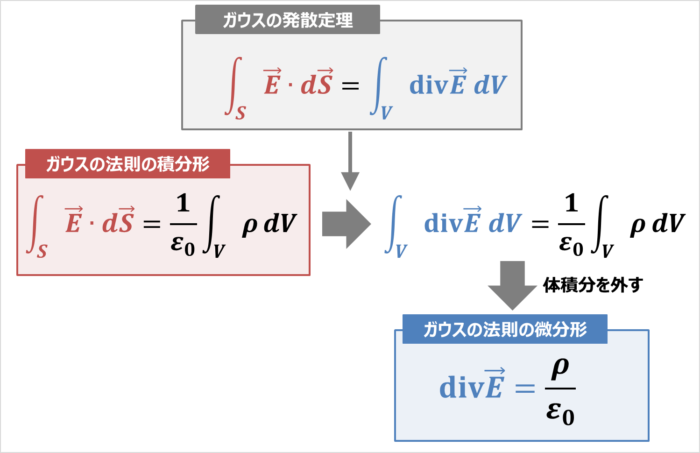
「ガウスの法則の積分形」は左辺が面積分、右辺が体積分となっています。

そのため、『面積分⇔体積分』の変換をする必要があります。

この変換にはガウスの法則の発散定理を用います。ガウスの発散定理とは、面積の積分(面積分)と体積の積分(体積分)の関係を表す公式であり、次式となります。

ガウスの発散定理の公式

\begin{eqnarray}
\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV
\end{eqnarray}

このガウスの法則の発散定理を用いて、「ガウスの法則の積分形」の左辺の面積分を体積分に変換すると次式となります。
\begin{eqnarray}
\displaystyle\int_S {\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}&=&\frac{1}{{\varepsilon}_0}\displaystyle\int_V {\rho}dV\\
{\Leftrightarrow}\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV&=&\frac{1}{{\varepsilon}_0}\displaystyle\int_V {\rho}dV\\
\end{eqnarray}

ここで、両辺とも体積分となるため、外すことできます。外すと「ガウスの法則の微分形」となり、次式となります。

ガウスの法則の微分形

\begin{eqnarray}
{\mathrm{div}}{\vec{E}}=\frac{{\rho}}{{\varepsilon}_0}
\end{eqnarray}

なお、ガウスの法則の発散定理については以下の記事でまとめています。