抵抗を買う際、売っている抵抗値を見てみると1kΩ,2kΩ,3kΩとなっているのではなく、1kΩ,2,2kΩ,4.7kΩと中途半端な数字になっていますよね。この中途半端な値はE系列という等比数列によって決まっているのです。
この記事ではこのE系列について詳しく説明します。
E系列の一覧表
まず最初に、E系列の一覧表を下表に示します。回路設計時などに参考していただくと幸いです。E系列はE3~E192まであります(表ではE96系列まで表示しています。E192まで入れようとすると膨大な表になってしまうので・・・)。
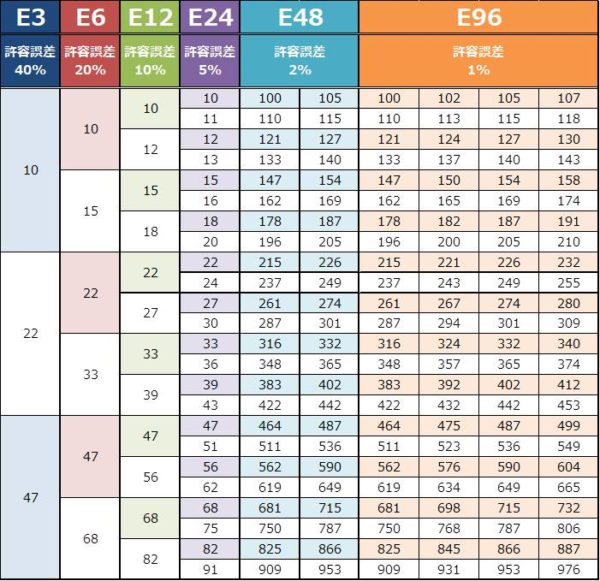
上表の見方ですが、例えば、E3系列は10、22、47となっていますね。これはE3系列である抵抗の抵抗値やコンデンサの容量値には、
があるということになります(桁が1桁あがるまでに3ステップあることからE3系列と呼ばれています)。
補足
E系列の計算方法
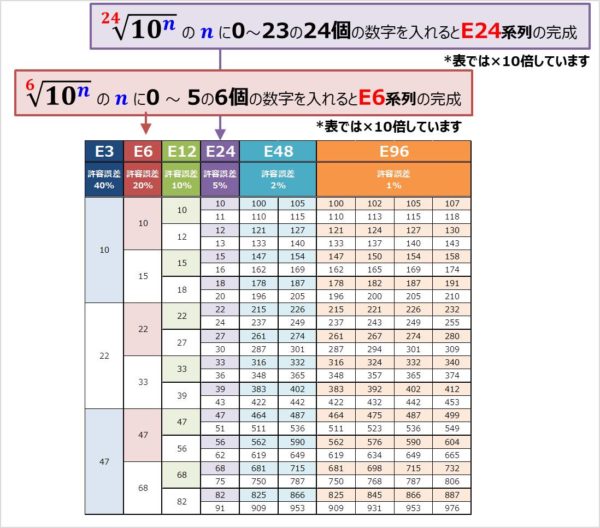
次のこのE系列の計算方法について説明します。例えば、上表のE6系列を見ると、
という値になっていますね。E6系列は\(\sqrt[6]{10^n}\)のnに0~5の6個の数字を入れると完成させることができます。一例として、nが0,1,2の時の計算結果を下に示します(*小数点を無くすために計算後×10倍しています)。
- nが0の時
- nが1の時
- nが2の時
\begin{eqnarray}
\sqrt[6]{10^0}×10=10.00
\end{eqnarray}
\begin{eqnarray}
\sqrt[6]{10^1}×10=14.67{\approx}15
\end{eqnarray}
\begin{eqnarray}
\sqrt[6]{10^2}×10=21.54{\approx}22
\end{eqnarray}
このように計算結果は上表のE6系列と一致していることが確認できます。なお、\(\sqrt[6]{10}\)は6回掛けると10になる数(10の6乗根)を表わします。
補足
- \(\sqrt[6]{10}\)を6乗すればぴったり10になるため、言い換えれば、E6系列とは1~10の範囲を等比級数\(\sqrt[6]{10}\)で分割したものとなります。
- 同様に、E24系列は\(\sqrt[24]{10^n}\)のnに0~23の24個の数字を入れると完成させることができます。
なぜE系列があるのか
そもそもなぜE系列があるのでしょうか。例えば、E24系列の場合、「10、11、12、13」と最初は1刻みに続きますが、13の次は14ではなく15となります。なんだか中途半端ですね。
これは、E系列は「製造時のバラツキ、温度変化、経年劣化などで生じる電子部品の誤差」を考慮して考えられた等比数列となっているからです。
電子部品の値の数は多いほど便利ですが、部品の製造者にとっては数が増えることによって管理が大変になります。例えば、抵抗値が
と1Ω刻みになっていると、1から10kΩまでの間に10000種類も必要になってしまいます。
そのため、電子部品の誤差によって、製造する電子部品の素子値を決めているのです。
後ほど詳しく説明しますが、許容誤差が5%の電子部品の値にはE24系列が使用されます。以下にE系列と許容誤差の関係を示します。
| E系列 | 許容誤差 |
| E3系列 | 許容誤差40% |
| E6系列 | 許容誤差20% |
| E12系列 | 許容誤差10% |
| E24系列 | 許容誤差5% |
| E48系列 | 許容誤差2% |
| E96系列 | 許容誤差1% |
では、ここで少し詳しく許容誤差が5%の電子部品の値にはE24系列が使用される理由について説明します。
例えば、E24系列の抵抗のラインナップは
のようになっています。
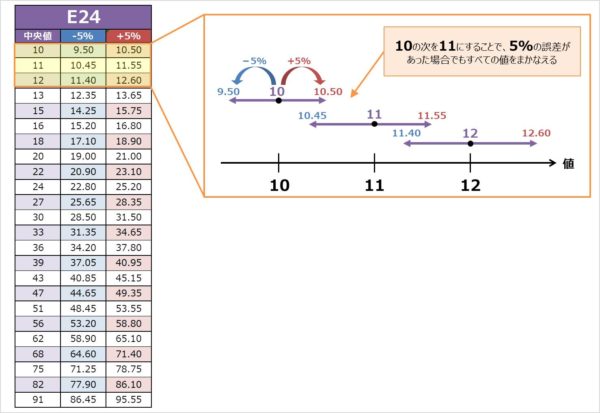
ここで、許容誤差5%の10Ω抵抗は9.50Ω(-5%)~10.50Ω(+5%)の範囲でバラツキがあります。また、許容誤差5%の11Ω抵抗は10.45Ω(-5%)~11.55Ω(+5%)の範囲でバラツキがあります。E系列はこの誤差範囲がお互いのカバー範囲になるようになっています。
では、11Ωがない場合を考えてみましょう。11Ωがない場合は、10Ωの次は12Ωとなりますね。
許容誤差5%の12Ω抵抗は11.40Ω(-5%)~12.60Ω(+5%)の範囲でバラツキが生じます。この場合、10.50Ωから11.40Ωをカバーすることができなくなります。これが、許容誤差が5%の電子部品にはE24系列が使用されている理由です。
補足
- JIS C5063という規格によって、各許容誤差でどのE系列を使用するかが決められています。
- 1%より精度の良い部品も製造されていますが、現在はほとんど受注生産になっている様です。
- 一般的に入手しやすいものはE3系列、E6系列、E12系列、E24系列なので、電気回路の設計ではこれらのE系列のものをなるべく使用するようにしましょう。
E系列の値と計算結果の誤差
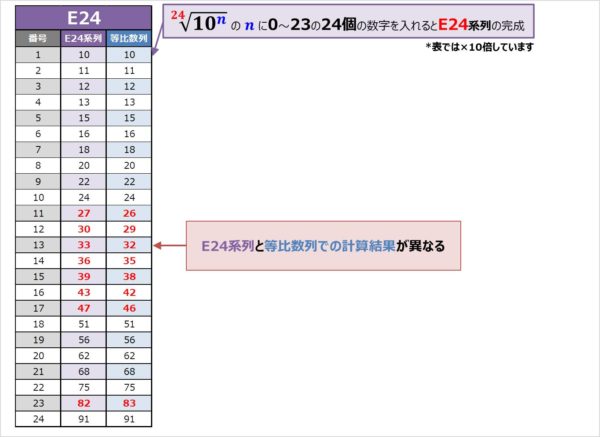
E24系列は\(\sqrt[24]{10^n}\)のnに0~23の24個の数字を入れると完成させることができますと言いましたが、厳密には計算結果と少し誤差があります。
上表はE24系列の値と\(\sqrt[24]{10^n}\)の式に0~23の24個の数字を入れた時の結果を示しています(*表では小数点を無くすために計算後×10倍しています)。
この表の赤字で書いた数字が一致していない箇所です。このようになる理由はよく分かりませんが、実用上便利だからという説もあります。
まとめ
この記事ではE系列について、一覧表や一覧表を作成するための計算方法などを説明しました。回路設計などに役になってくれると幸いです。
当サイトの全記事はこちらから!






