交流回路において、理想的なコンデンサの消費電力はゼロになります。
どうして、電流が流れているのに消費電力がゼロになるのでしょうか?
この記事では、コンデンサの消費電力がゼロになる理由を『式』と『波形』で説明します。図を用いて分かりやすく説明するように心掛けていますので、ご参考になれば幸いです。
コンデンサの消費電力がゼロになる理由を『式』で説明
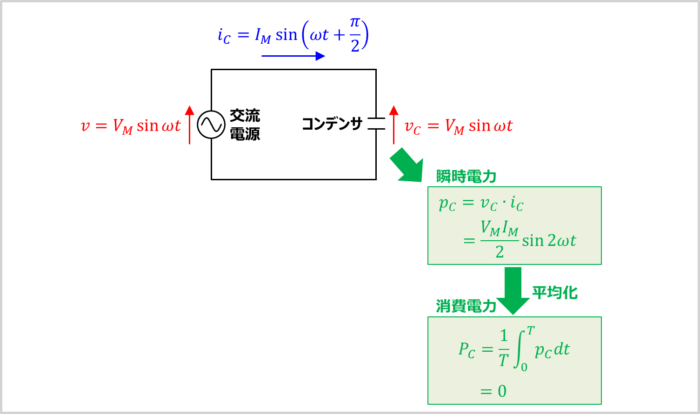
理想的なコンデンサの消費電力がゼロになる理由を『式』で説明します。
コンデンサの消費電力は下記の手順(ステップ1,2)で求めることができます。
コンデンサの消費電力を求める手順
- コンデンサの瞬時電力\(p_C\)を求める。
- 瞬時電力\(p_C\)を1周期で積分して平均化する。
ではこれから、コンデンサの消費電力を計算してゼロになるのを確かめてみましょう。
上図に示しているのは、交流電源\(v\)にコンデンサのみを接続している回路です。
交流電源の電圧の最大値を\(V_M{\mathrm{[V]}}\)、角周波数を\({\omega}{\mathrm{[rad/s]}}\)、時間を\(t{\mathrm{[s]}}\)とすると、交流電源\(v\)は次式で表されます。
\begin{eqnarray}
v=V_M{\sin}{\omega}t{\;}{\mathrm{[V]}}\tag{1}
\end{eqnarray}
上図に示している回路は交流電源\(v\)にコンデンサのみを接続しています。そのため、コンデンサにかかる電圧\(v_C\)は交流電源\(v\)と等しくなるため、次式が成り立ちます。
\begin{eqnarray}
v_C=v=V_M{\sin}{\omega}t{\;}{\mathrm{[V]}}\tag{2}
\end{eqnarray}
「コンデンサに流れる電流\(i_C\)」は「コンデンサにかかる電圧\(v_C\)」よりも位相が\(90^{\circ}\left(\displaystyle\frac{{\pi}}{2}{\mathrm{rad}}\right)\)進みます。そのため、コンデンサに流れる電流の最大値を\(I_M{\mathrm{[A]}}\)とすると、コンデンサに流れる電流\(i_C\)は次式で表されます。
\begin{eqnarray}
i_C=I_M{\sin}\left({\omega}t+\frac{{\pi}}{2}\right){\mathrm{[A]}}\tag{3}
\end{eqnarray}
あわせて読みたい
「コンデンサに流れる電流\(i_C\)」が「コンデンサにかかる電圧\(v_C\)」よりも位相が\(90^{\circ}\left(\displaystyle\frac{{\pi}}{2}{\mathrm{rad}}\right)\)進む理由については、下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る
コンデンサに流れる電流の位相が進む理由
コンデンサの瞬時電力\(p_C{\mathrm{[W]}}\)は「(2)式の\(v_C\)」と「(3)式の\(i_C\)」の積となるため、次式で表されます。
\begin{eqnarray}
p_C&=&v_C{\;}{\cdot}{\;}i_C\\
\\
&=&V_M{\sin}{\omega}t{\;}{\cdot}{\;}I_M{\sin}\left({\omega}t+\frac{{\pi}}{2}\right)\\
\\
&=&V_MI_M{\sin}{\omega}t{\;}{\sin}\left({\omega}t+\frac{{\pi}}{2}\right){\mathrm{[W]}}\tag{4}
\end{eqnarray}
ここで、(4)式を少し整理してみましょう。
まず、三角関数の加法定理を用いると、(4)式にある「sin」は次式に変形することができます。
\begin{eqnarray}
{\sin}\left({\omega}t+\frac{{\pi}}{2}\right)&=&{\sin}{\omega}t{\;}{\cos}\frac{{\pi}}{2}+{\cos}{\omega}t{\;}{\sin}\frac{{\pi}}{2}\\
\\
&=&{\sin}{\omega}t{\;}{\cdot}{\;}0+{\cos}{\omega}t{\;}{\cdot}{\;}1\\
\\
&=&{\cos}{\omega}t\tag{5}
\end{eqnarray}
【参考】三角関数の加法定理
\begin{eqnarray}
{\sin}(α+β)&=&{\sin}α{\;}{\cos}β+{\cos}α{\;}{\sin}β\\
\\
{\sin}(α-β)&=&{\sin}α{\;}{\cos}β-{\cos}α{\;}{\sin}β\\
\\
{\cos}(α+β)&=&{\cos}α{\;}{\cos}β-{\sin}α{\;}{\sin}β\\
\\
{\cos}(α-β)&=&{\cos}α{\;}{\cos}β+{\sin}α{\;}{\sin}β\\
\\
{\tan}(α+β)&=&\frac{{\tan}α+{\tan}β}{1-{\tan}α{\;}{\tan}β}\\
\\
{\tan}(α-β)&=&\frac{{\tan}α-{\tan}β}{1+{\tan}α{\;}{\tan}β}
\end{eqnarray}
そのため、(5)式を(4)式に代入すると、コンデンサの瞬時電力\(p_C{\mathrm{[W]}}\)は次式となります。
\begin{eqnarray}
p_C&=&V_MI_M{\sin}{\omega}t{\;}{\sin}\left({\omega}t+\frac{{\pi}}{2}\right)\\
\\
&=&V_MI_M{\sin}{\omega}t{\;}{\cos}{\omega}t{\;}{\mathrm{[W]}}\tag{6}
\end{eqnarray}
(6)式に三角関数の倍角公式を用いると、コンデンサの瞬時電力\(p_C{\mathrm{[W]}}\)は次式に変形することができます。
\begin{eqnarray}
p_C&=&V_MI_M{\sin}{\omega}t{\;}{\cos}{\omega}t\\
\\
&=&V_MI_M{\;}{\cdot}{\;}\frac{{\sin}2{\omega}t}{2}\\
\\
&=&\frac{V_MI_M}{2}{\sin}2{\omega}t{\;}{\mathrm{[W]}}\tag{7}
\end{eqnarray}
【参考】三角関数の倍角公式
\begin{eqnarray}
{\sin}2α&=&{\sin}α{\;}{\cos}α+{\cos}α{\;}{\sin}α\\
\\
&=&2{\sin}α{\;}{\cos}α\\
\\
{\Leftrightarrow}{\sin}α{\;}{\cos}α&=&\frac{{\sin}2α}{2}
\end{eqnarray}
(7)式をコンデンサにかかる電圧\(v_C\)の1周期\(T\)で積分して、平均したものがコンデンサの消費電力(平均電力)\(P_C{\mathrm{[W]}}\)となります。そのため、消費電力\(P_C\)は次式となります。
\begin{eqnarray}
P_C&=&\frac{1}{T}{\displaystyle\int}_0^Tp_Cdt\\
\\
&=&\frac{1}{T}{\displaystyle\int}_0^T\left(\frac{V_MI_M}{2}{\sin}2{\omega}t\right)dt\tag{8}
\end{eqnarray}
ここで、\({\omega}=2{\pi}f\)を用いると、周期\(T\)は次式で表すことができます。
\begin{eqnarray}
T=\frac{1}{f}=\frac{2{\pi}}{{\omega}}\tag{9}
\end{eqnarray}
(9)式を(8)式に代入すると、消費電力\(P_C\)は次式となります。
\begin{eqnarray}
P_C&=&\frac{1}{\displaystyle\frac{2{\pi}}{{\omega}}}{\displaystyle\int}_0^{\displaystyle\frac{2{\pi}}{{\omega}}}\left(\frac{V_MI_M}{2}{\sin}2{\omega}t\right)dt\\
\\
&=&\frac{{\omega}}{2{\pi}}{\;}{\cdot}{\;}\frac{V_MI_M}{2}{\displaystyle\int}_0^{\displaystyle\frac{2{\pi}}{{\omega}}}{\sin}2{\omega}t{\;}dt\\
\\
&=&\frac{{\omega}V_MI_M}{4{\pi}}{\displaystyle\int}_0^{\displaystyle\frac{2{\pi}}{{\omega}}}{\sin}2{\omega}t{\;}dt\\
\\
&=&\frac{{\omega}V_MI_M}{4{\pi}}\left[-\frac{{\cos}2{\omega}t}{2{\omega}}\right]_0^{\displaystyle\frac{2{\pi}}{{\omega}}}\\
\\
&=&-\frac{{\omega}V_MI_M}{4{\pi}{\;}{\cdot}{\;}2{\omega}}\left[{\cos}2{\omega}t\right]_0^{\displaystyle\frac{2{\pi}}{{\omega}}}\\
\\
&=&-\frac{V_MI_M}{8{\pi}}\left\{{\cos}\left(2{\omega}{\;}{\cdot}{\;}\frac{2{\pi}}{{\omega}}\right)-{\cos}\left(2{\omega}{\;}{\cdot}{\;}0\right)\right\}\\
\\
&=&-\frac{V_MI_M}{8{\pi}}\left({\cos}4{\pi}-{\cos}0\right)\\
\\
&=&-\frac{V_MI_M}{8{\pi}}\left(1-1\right)\\
\\
&=&0{\;}{\mathrm{[W]}}\tag{10}
\end{eqnarray}
(10)式から分かるように、計算すると、コンデンサの消費電力\(P_C\)がゼロになることが分かります。
では次に、理想的なコンデンサの消費電力がゼロになる理由を『波形』で説明します。
補足
- 消費電力は『有効電力』とも呼ばれています。
コンデンサの消費電力がゼロになる理由を『波形』で説明
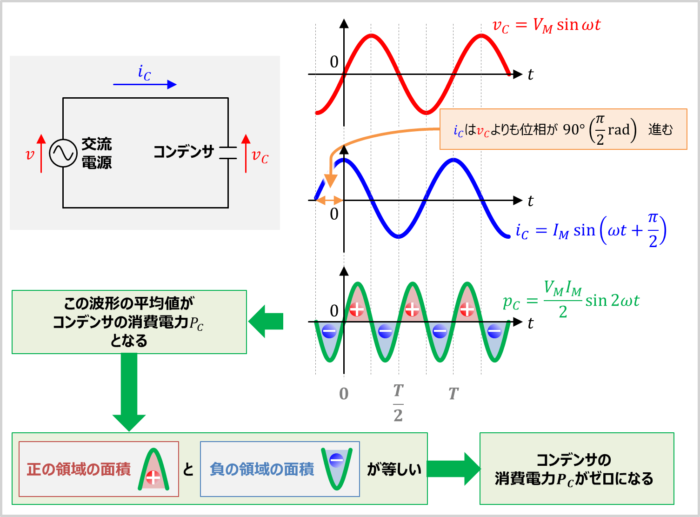

先ほど、「コンデンサにかかる電圧\(v_C\)」と「コンデンサに流れる電流\(i_C\)」と「コンデンサの瞬時電力\(p_C\)」を計算で求めました。
- コンデンサにかかる電圧\(v_C\)
\begin{eqnarray}
v_C=V_M{\sin}{\omega}t{\;}{\mathrm{[V]}}
\end{eqnarray} - コンデンサに流れる電流\(i_C\)
\begin{eqnarray}
i_C=I_M{\sin}\left({\omega}t+\frac{{\pi}}{2}\right){\mathrm{[A]}}
\end{eqnarray} - コンデンサの瞬時電力\(p_C\)
\begin{eqnarray}
p_C=\frac{V_MI_M}{2}{\sin}2{\omega}t{\;}{\mathrm{[W]}}
\end{eqnarray}
これらの式を波形で描くと上図のようになります。
「コンデンサの瞬時電力\(p_C\)」は最大値が「\(\displaystyle\frac{V_MI_M}{2}\)」の正弦波となり、周波数は「コンデンサにかかる電圧\(v_C\)」や「コンデンサに流れる電流\(i_C\)」の2倍となります。そのため、「コンデンサの瞬時電力\(p_C\)」の1周期は\(\displaystyle\frac{T}{2}\)となります。
この瞬時電力\(p_C\)の平均値が、コンデンサの消費電力\(P_C\)となります。
ここで、「コンデンサの瞬時電力\(p_C\)」の波形を見ると、正と負を繰り返しています。また、「正の領域の面積」と「負の領域の面積」は等しくなります。そのため、「コンデンサの瞬時電力\(p_C\)」を平均するとゼロになります。すなわち、コンデンサの消費電力\(P_C\)がゼロになります。
ちなみに、コンデンサの瞬時電力\(p_C\)が正の時は交流電源\(v\)がコンデンサに電力を送っています。一方、コンデンサの瞬時電力\(p_C\)が負の時はコンデンサが交流電源\(v\)に電力を送り返しています。交流電源\(v\)が電力を送っても全て送り返されるので、この電力は「無効電力」と呼ばれています。
あわせて読みたい
交流回路の電力には「有効電力(消費電力)」・「無効電力」・「皮相電力」があります。各用語の違いについては下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る


有効電力・無効電力・皮相電力の違いを分かりやすく解説します!
補足
- (8)式ではコンデンサにかかる電圧\(v_C\)の1周期\(T\)で積分して、平均することで、コンデンサの消費電力\(P_C\)を求めましたが、コンデンサの瞬時電力\(p_C\)の1周期\(\displaystyle\frac{T}{2}\)で積分して、平均しても、コンデンサの消費電力\(P_C\)を求めることができます。
コンデンサの瞬時電力\(p_C\)の波形の描き方
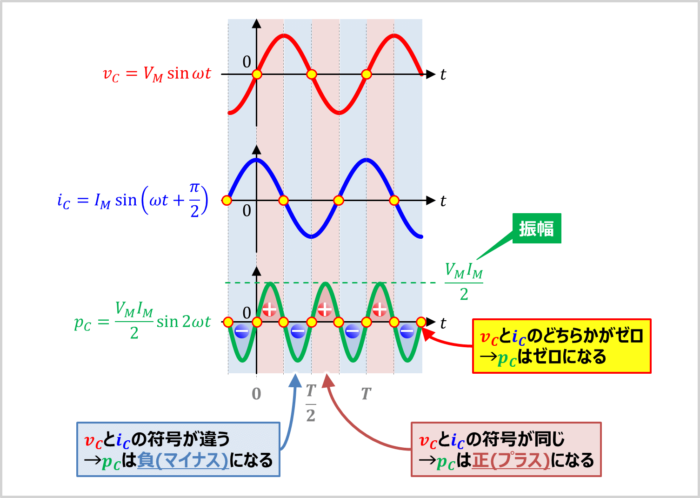

コンデンサの瞬時電力\(p_C\)の波形の描き方についてもう少し詳しく説明します。
- 「電圧\(v_C\)」と「電流\(i_C\)」の符号が違う時(片方が「正」で片方が「負」の時)
- 「瞬時電力\(p_C\)」は負(マイナス)になります。
- 「電圧\(v_C\)」と「電流\(i_C\)」の符号が同じ時(両方が「正」または「負」の時)
- 「瞬時電力\(p_C\)」は正(プラス)になります。
- 「電圧\(v_C\)」と「電流\(i_C\)」のどちらかがゼロの時
- 「瞬時電力\(p_C\)」はゼロになります。
なお、「瞬時電力\(p_C\)」の振幅は(7)式より「\(\displaystyle\frac{V_MI_M}{2}\)」になります。
まとめ
この記事では『コンデンサの消費電力がゼロになる理由』について、以下の内容を説明しました。
- コンデンサの消費電力がゼロになる理由を『式』で説明
- コンデンサの消費電力がゼロになる理由を『波形』で説明
- コンデンサの瞬時電力\(p_C\)の波形の描き方
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






