トランスを設計するときに重要なパラメータの1つである『AL値』。
コア(鉄心)の形状やサイズが記載してあるデータシートを見ると『AL値』が書いてありますが、これが何を意味しているのかご存知でしょうか。
今回は、このAL値について『AL値とは?』の基本的な内容から、『AL値の計算方法』などを説明したいと思います。
AL値とは
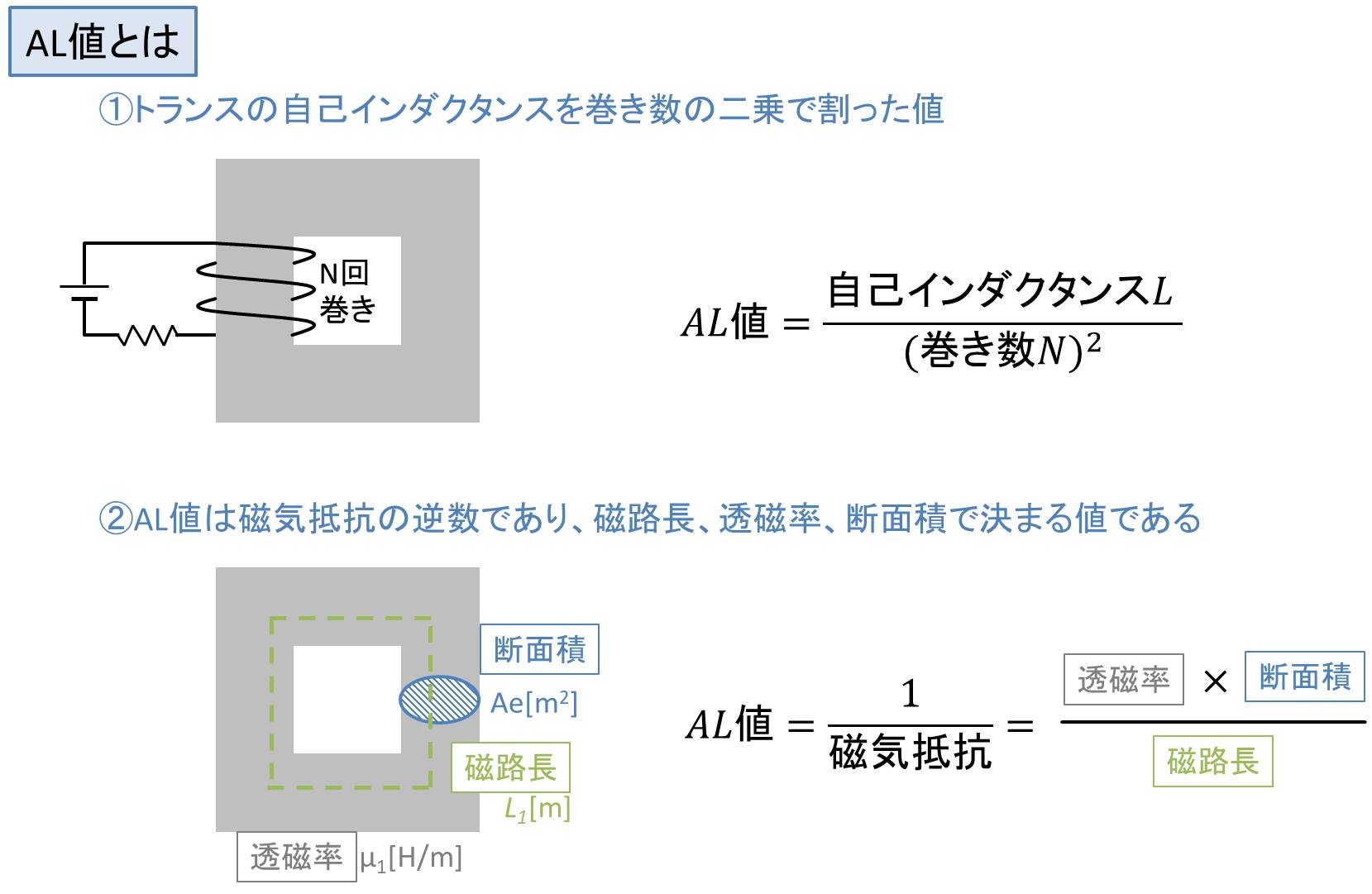
AL値とは『トランスの自己インダクタンスを巻き数の2乗で割った値』です。単位は通常は [nH/N2]で表します。
これは逆に言えば、トランスを作製するときに、AL値が分かると、何巻きすればどれくらいの自己インダクタンスになるかが分かるということです。
例えば、AL値が2000[nH/N2]のコアがあるとすると、このコアに対して100回巻けば、自己インダクタンスは2000[nH/N2]×100[N]×100[N]=0.02[H]となります。AL値が大きいほど、少ない巻き数で大きな自己インダクタンスを得ることができます。
また、AL値は磁気抵抗の逆数であり、コアの磁路長、透磁率、断面積で決まります。
なお、このAL値は『インダクション係数』や『AL-value』とも呼ばれています。
AL値の求め方
AL値はコアに『ギャップがない時』と『ギャップがある時』で式が異なります。
ギャップがない時のAL値
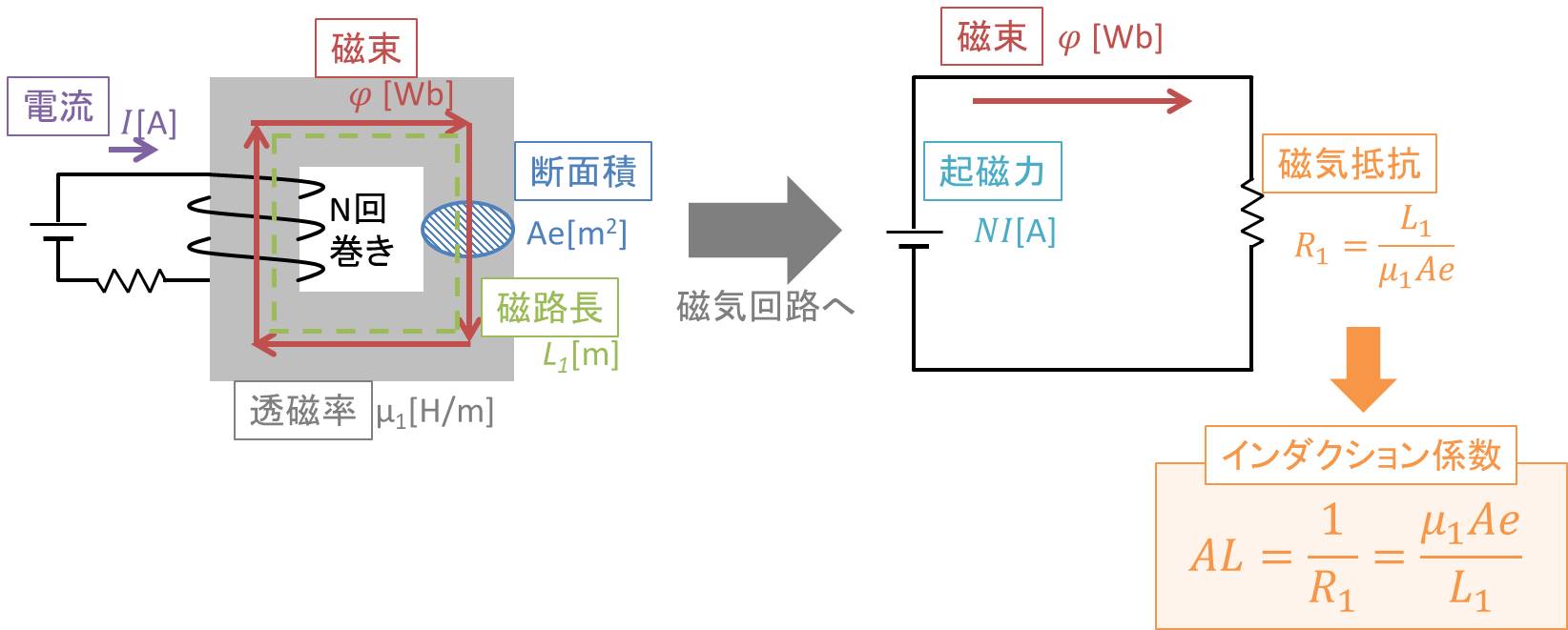
磁路長L1[m]、透磁率μ1[H/m]、断面積Ae[m2]のコアがあるとします。そのコアに対して、コイルをN回巻きにして、電流をI[A]流した時に、磁束がφ[Wb]発生した場合を考えてみます。
これを磁気回路に変換すると、磁気回路は起磁力NI[A]、磁束φ[Wb]、磁気抵抗R1となります。磁気抵抗R1は磁路長L1[m]に比例し、断面積Ae[m 2 ]と透磁率μ1[H/m]に反比例するため、
磁気抵抗R1は
$$ R_1=\frac{L_1}{{μ_1}Ae}$$
で表されます。なお磁気抵抗の単位は[H -1 ]か[A/Wb]です。
AL値は磁気抵抗R1の逆数なので、ギャップがない時のAL値は
$$ AL =\frac{1}{R_1}\frac{{μ_1}Ae }{ L_1}$$
となります。
ギャップがある時のAL値
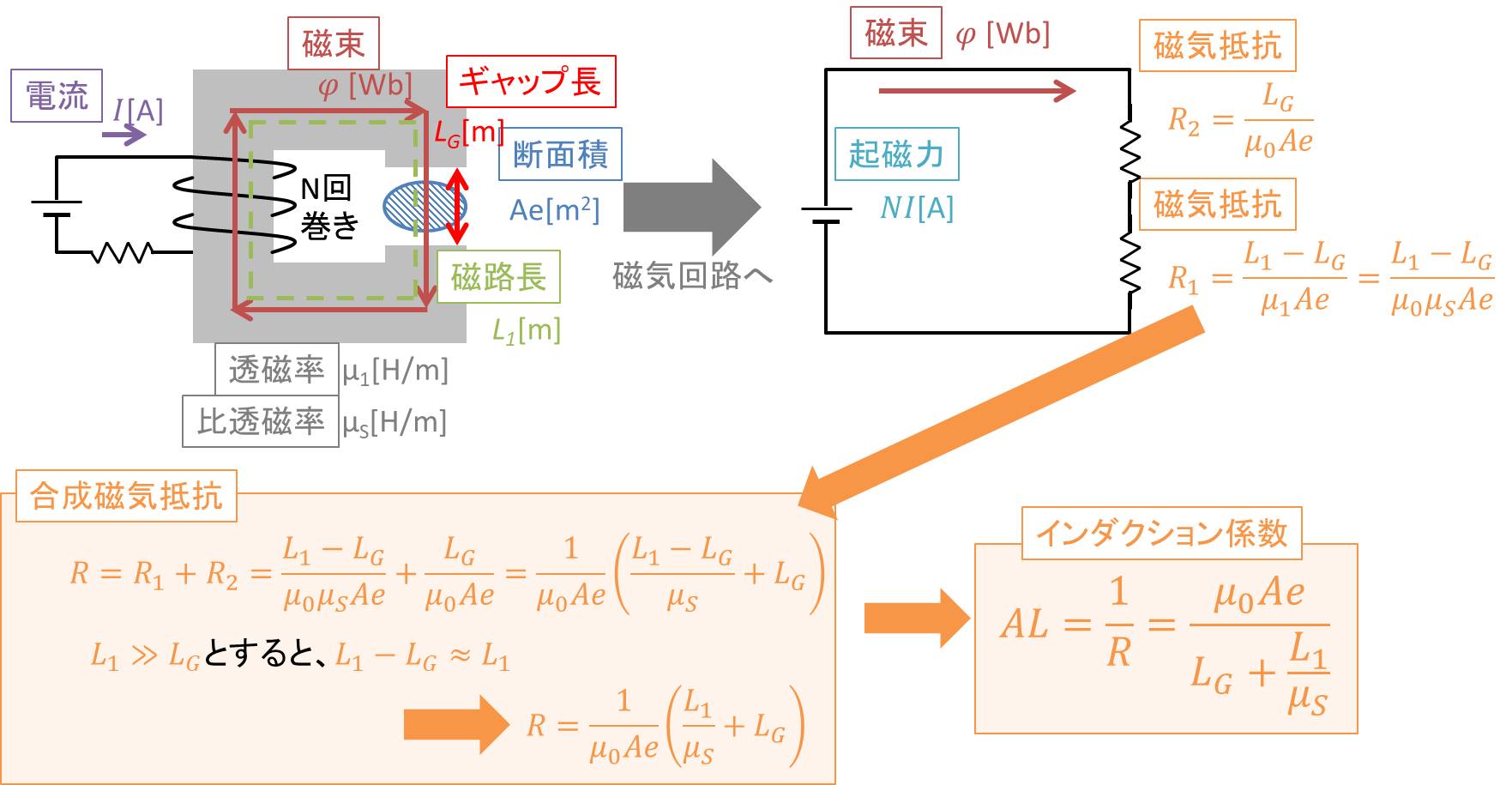
同じようにして、ギャップがある時のAL値を求めてみます。
LG[m]のギャップが開いている、磁路長L1[m]、透磁率μ1[H/m]、比透磁率μS、断面積Ae[m 2 ]のコアがあるとします。そのコアに対して、コイルをN回巻きにして、電流をI[A]流した時に、磁束がφ[Wb]発生した場合を考えてみます。
これを磁気回路に変換すると、磁気回路は起磁力NI[A]、磁束φ[Wb]、コアの磁気抵抗R1、ギャップの磁気抵抗R2となります。合成磁気抵抗Rは電気回路と同じくコアの磁気抵抗R1とギャップの磁気抵抗R2の直列接続となります。
コアの磁気抵抗R1は磁路長L1[m]にギャップ長LG[m]を引いた(L1-LG) [m]に比例し、断面積Ae[m^2]とコアの透磁率μ1[H/m]に反比例します。また、ギャップ部分の磁気抵抗R2はギャップ長LG[m]に比例し、断面積Ae[m^2]と空気の透磁率μ0[H/m]に反比例します。そのため、合成磁気抵抗Rは、
$$ R={R_1}+{R_2}=\frac{{L_1}-{L_G}}{{μ_1}Ae}+\frac{L_G}{{μ_0}Ae}=\frac{{L_1}-{L_G}}{{μ_0}{μ_S}Ae}+\frac{L_G}{{μ_0}Ae}=\frac{1}{{μ_0}Ae}(\frac{{L_1}-{L_G}}{μ_S }+{L_G })$$
で表されます。ここで、磁路長L1[m]はギャップ長LG[m]より十分大きいとすると、
$${L_1}-{L_G}{\approx }{L_1}$$
と近似でき、合成磁気抵抗Rは、
$$ R=\frac{1}{{μ_0}Ae}(\frac{L_1}{μ_S}+{L_G})$$
となります。
AL値は合成磁気抵抗Rの逆数なので、ギャップがある時のAL値は
$$ AL =\frac{1}{R}=\frac{{μ_0}Ae }{{L_G }+\frac{L_1}{μ_S}}$$
となります。
ギャップがある時のAL値を近似する
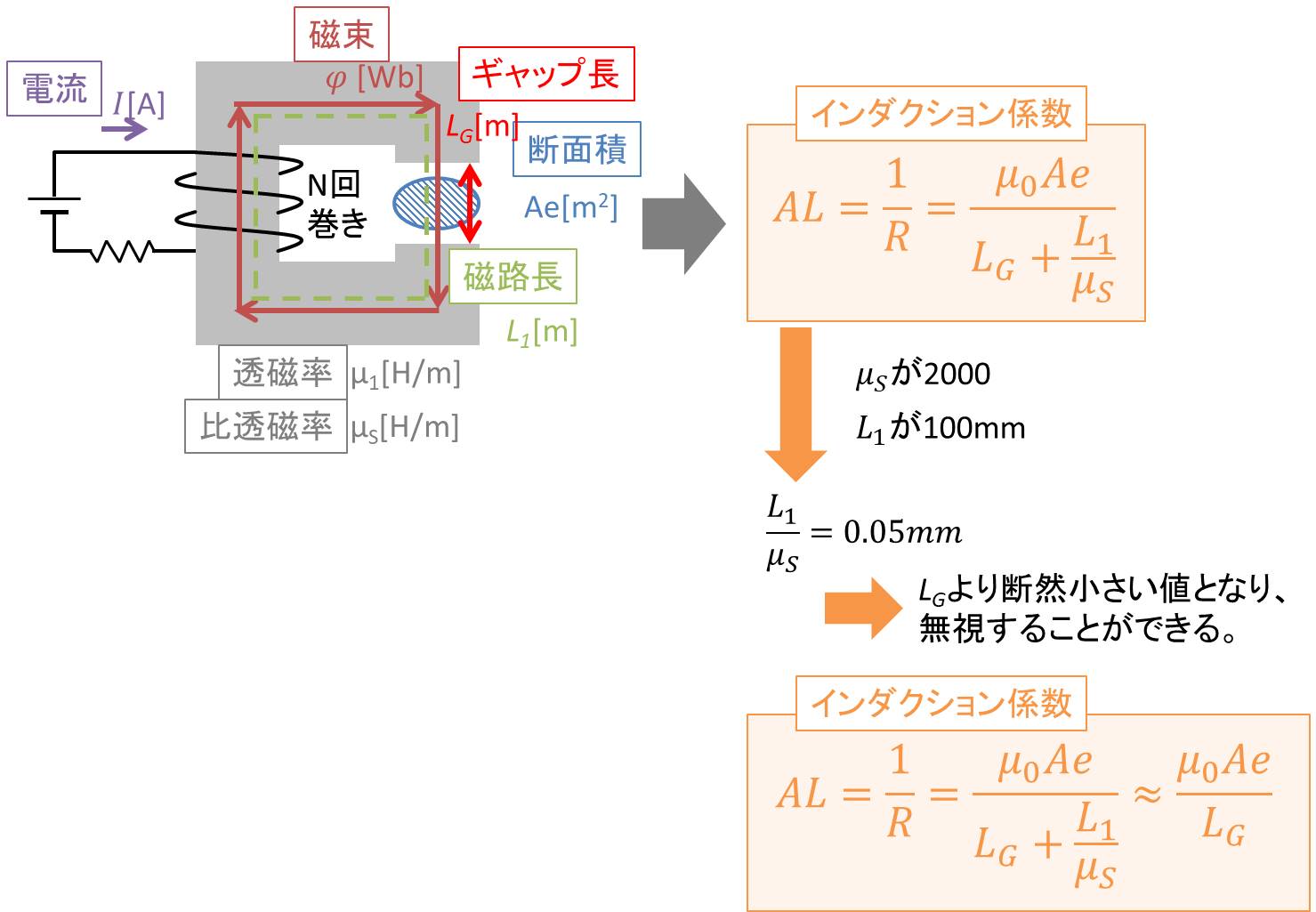
スイッチング電源で使用するような小型フェライトコアの場合、比透磁率は1500~4000程度で、磁路長は20[mm]~200[mm]であることが多いです。
例えば、磁路長100[mm]で比透磁率を2000とすると、L1/μS=0.05mmとなり、ギャップ長LGに対して非常に小さくなります。そのため、ギャップ長LGが0.05mmを大きく超えるような場合には、L1/usはLGに対して無視できる値になります。
この場合、AL値は
$$ AL =\frac{1}{R}=\frac{{μ_0}Ae }{{L_G }+\frac{L_1}{μ_S}}{\approx }\frac{{μ_0}Ae }{{L_G }}$$
となり、ギャップ長が長い場合には、AL値の式にコアの透磁率が入らなくなります。これはつまり、ギャップ長がある場合、AL値はコアの材質に依存しない値になるということです。
このようにコアにギャップがあることで、透磁率が大幅に変わります。コアクラックが致命的なのはこの理由です。
実際のデータシートを見てみよう
コア材のデータシート
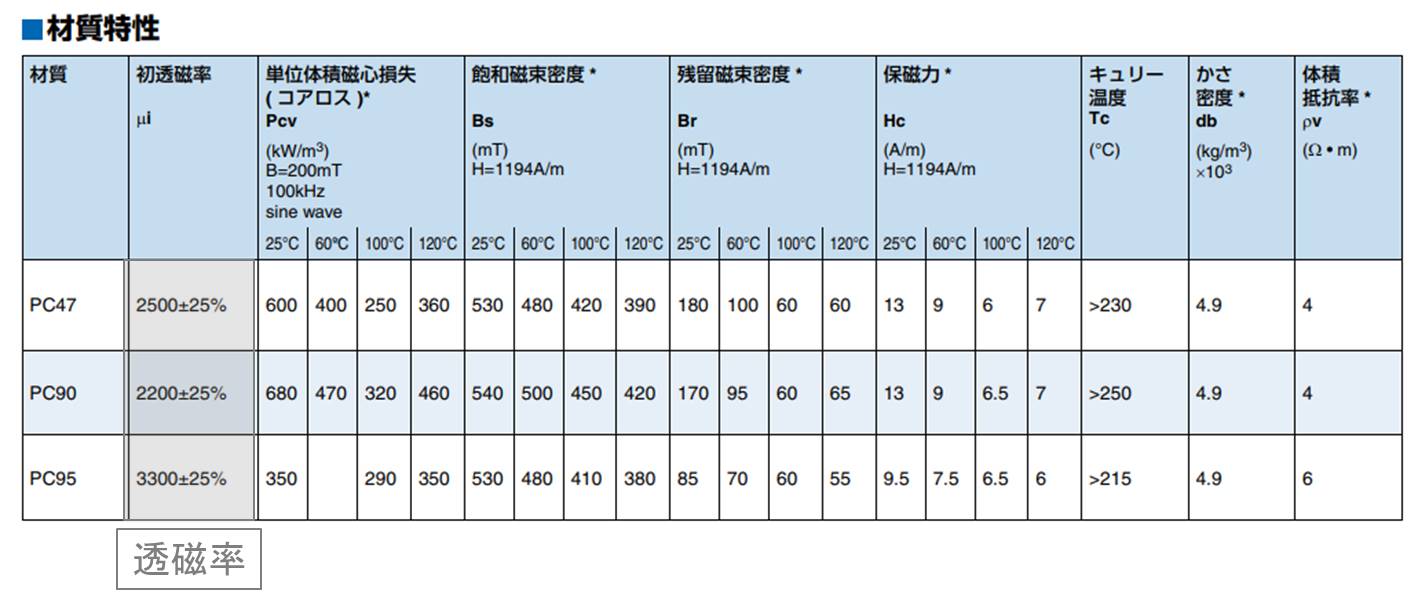
これはTDKさんのコア材のデータシートです。コア材には透磁率が記載されていますね。透磁率を見ると±25%と記載があるように、フェライトコアの透磁率はばらつきがあります。計算で求めた後に別途、調整が必要です。
コア形状のデータシート
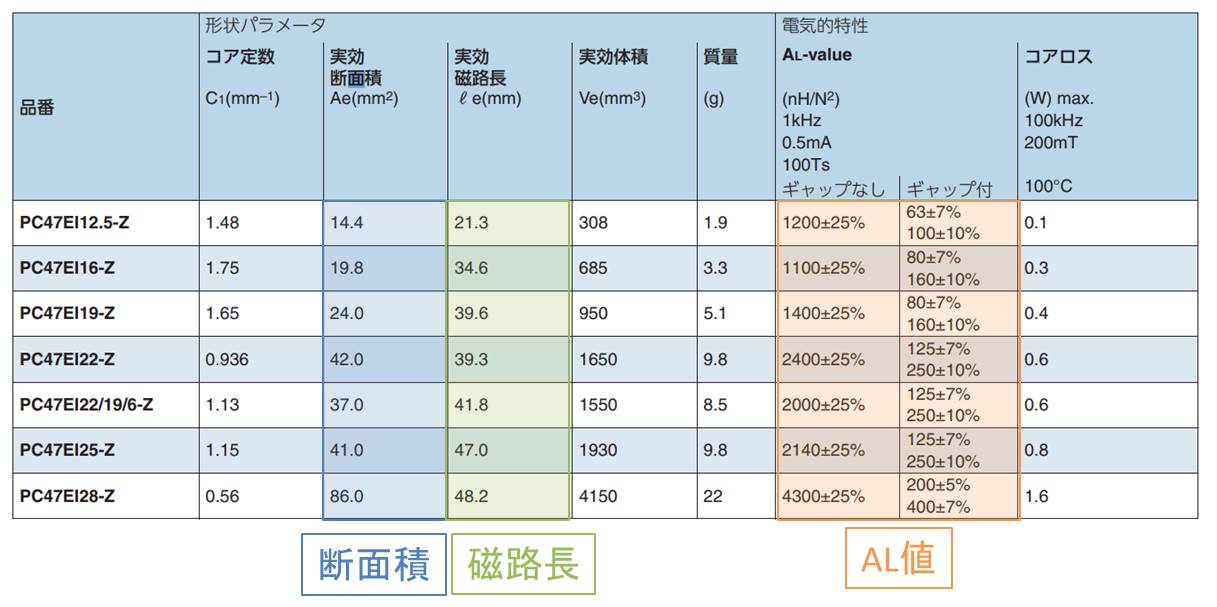
次は、コア形状のデータシートです。コアの断面積、磁路長、AL値が記載されています。このようにAL値はデータシートに記載されているので、巻き数さえ決まれば、自己インダクタンスがどれくらいの値になるか把握することができるのです。






