『アドミタンス』と『コンダクタンス』と『サセプタンス』の違い！

電気の流れやすさを表すものとして『アドミタンス』と『コンダクタンス』と『サセプタンス』があります。

これらの用語の違いをご存知でしょうか。

この記事では『アドミタンス』と『コンダクタンス』と『サセプタンス』の定義と違いについて、式や図を用いて分かりやすく説明しています。ご参考になれば幸いです。

『アドミタンス』と『コンダクタンス』と『サセプタンス』の違い

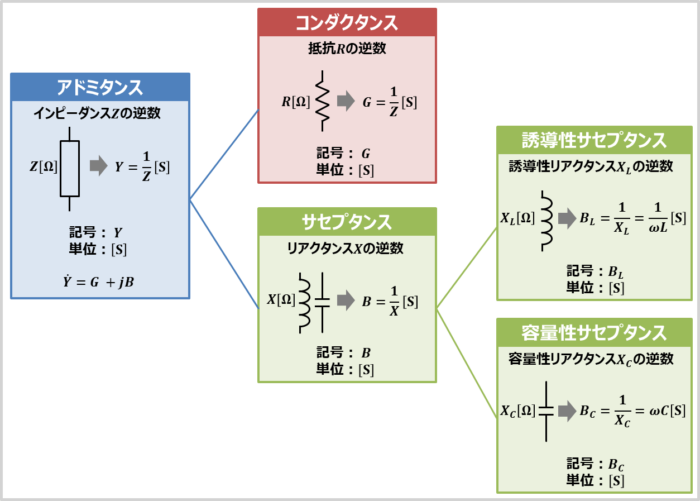
最初に『アドミタンス』と『コンダクタンス』と『サセプタンス』の違いを下記にまとめます。後ほど各用語について詳しく説明しますので、下記は飛ばして読んでもOKです。

アドミタンス
- インピーダンスZの逆数であり、電流の流れやすさの総称です。記号は「Y」、単位は[S]を用います。また、アドミタンスYはコンダクタンスGとサセプタンスBを合わせたものであり、式では「Y=G+jB」と表します。そのため、アドミタンスの実数部がコンダクタンスGであり、虚数部がサセプタンスBとなります。
コンダクタンス
- 抵抗Rの逆数であり、直流または交流回路における電流の流れやすさを表したものです。記号は「G」、単位は[S]を用います。
サセプタンス
- リアクタンスXの逆数であり、交流回路における電流の流れやすさを表したものです。記号は「B」、単位は[S]を用います。

ではこれから各用語について順番に詳しく説明していきます。

アドミタンスとは

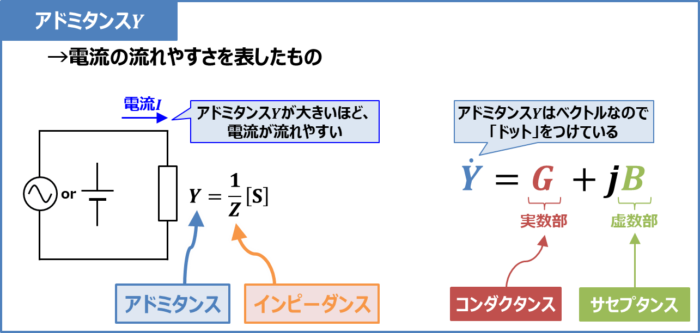
アドミタンスはインピーダンスZの逆数(1/Z)です。記号は「Y」、単位は[S](←ジーメンスと読む)となります。式で表すと次式となります。

\begin{eqnarray}
Y=\frac{1}{Z}{\mathrm{[S]}}
\end{eqnarray}

例えば、インピーダンスがZ=100[Ω]の時、アドミタンスはY=0.01[S]となります。

インピーダンスZは電流の流れにくさを表します。インピーダンスZが大きいほど電流が流れにくくなります。一方、アドミタンスYはインピーダンスZの逆数なので、電流の流れやすさを表しています。アドミタンスYが大きいほど、電流が流れやすくなります。

また、アドミタンスYは後ほど説明するコンダクタンスGとサセプタンスBを合わせたものであり、式を用いると次式で表すことができます。

\begin{eqnarray}
{\dot{Y}}=G+jB
\end{eqnarray}

すなわち、アドミタンスYの実数部がコンダクタンスGであり、虚数部がサセプタンスBとなります。

アドミタンスのポイント

インピーダンスZの逆数である。
記号は「Y」、単位は[S]を用いる。
アドミタンスYが大きいほど、電流が流れやすくなる。
アドミタンスYの実数部がコンダクタンスGであり、虚数部がサセプタンスBである。

アドミタンスの記号がYの理由

アドミタンスは英語では「Admittance」と書きますが、記号は「A」ではなく「Y」を用います。

「A」は電流の単位記号ですでに用いられているため使用することができないからであり、A～Zのアルファベットのうち使用されていなかったものが「Y」なので、アドミタンスの記号が「Y」になったというのが有力です。

電気記号について詳しくは下記の記事に記載しているのでご参考になれば幸いです。

: 『変数・図記号・単位』の由来と意味について！電流が『I』、トランジスタが『Q』なのはなぜ？
続きを見る

コンダクタンスとは

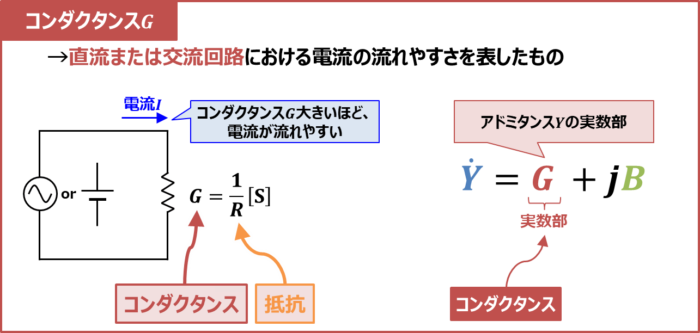
コンダクタンスは抵抗(レジスタンス)Rの逆数です。記号は「G」、単位は[S]となります。式で表すと次式となります。

\begin{eqnarray}
G=\frac{1}{R}{\mathrm{[S]}}
\end{eqnarray}

例えば、抵抗がR=10[Ω]の時、コンダクタンスはG=0.1[S]となります。

抵抗Rは直流または交流回路における電流の流れにくさを表します。抵抗Rが大きいほど、電流が流れにくくなります。一方、コンダクタンスGは抵抗Rの逆数なので、直流または交流回路における電流の流れやすさを表しています。コンダクタンスGが大きいほど、電流が流れやすくなります。

また、コンダクタンスGはアドミタンス(Y=G+jB)の実数部となります。

コンダクタンスのポイント

抵抗Rの逆数である。
記号は「G」、単位は[S]を用いる。
コンダクタンスGが大きいほど、電流が流れやすくなる。
アドミタンス(Y=G+jB)の実数部である。

コンダクタンスの記号がGの理由

コンダクタンスは英語では「Conductance」と書きますが、記号は「C」ではなく「G」を用います。

「C」はコンデンサの記号ですでに用いられているため使用することができないからであり、A～Zのアルファベットのうち使用されていなかったものが「G」なので、コンダクタンスの記号が「G」になったというのが有力です。

サセプタンスとは

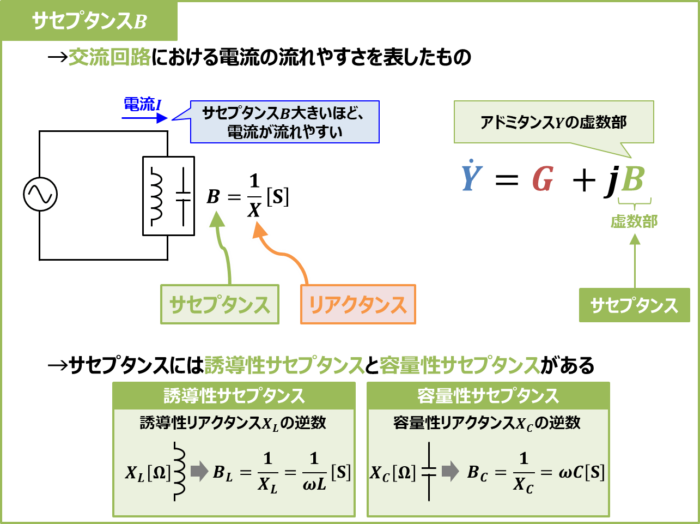
サセプタンスはリアクタンスXの逆数です。記号は「B」、単位は[S]となります。式で表すと次式となります。

\begin{eqnarray}
B=\frac{1}{X}{\mathrm{[S]}}
\end{eqnarray}

例えば、リアクタンスがX=10[Ω]の時、サセプタンスはB=0.1[S]となります。

リアクタンスXは交流回路における電流の流れやすさを表します。リアクタンスXが大きいほど、電流が流れにくくなります。一方、サセプタンスBはリアクタンスXの逆数なので、交流回路における電流の流れやすさを表しています。サセプタンスBが大きいほど、電流が流れやすくなります。

サセプタンスBはアドミタンス(Y=G+jB)の虚数部となります。

また、リアクタンスには『コイルのリアクタンス(誘導性リアクタンス)X_L』と『コンデンサのリアクタンス(容量性リアクタンス)X_C』の2種類あります。同様に、サセプタンスにも『コイルのサセプタンス(誘導性サセプタンス)B_L』と『コンデンサのサセプタンス(容量性サセプタンス)B_C』があり、次式の関係があります。

\begin{eqnarray}
B_L&=&\frac{1}{X_L}=\frac{1}{{\omega}L}{\mathrm{[S]}}\\
B_C&=&\frac{1}{X_C}={\omega}C{\mathrm{[S]}}
\end{eqnarray}

サセプタンスのポイント