【クーロンの法則】『公式』や『比例定数』や『歴史』などを解説！

この記事ではクーロンの法則、クーロンの法則の公式、クーロンの法則に出てくる比例定数k、歴史、万有引力の法則との違いなどを分かりやすく説明しています。

まず電荷間に働く力の向きから

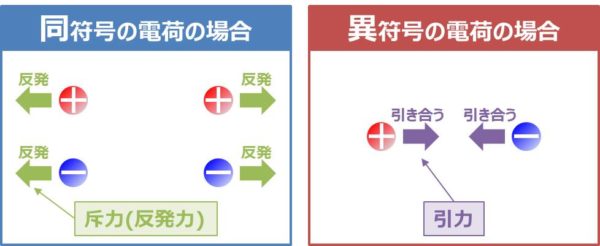
電荷にはプラス(+)の電荷である正電荷とマイナス(-)の電荷である負電荷があります。

正電荷の近くに正電荷を置いた場合どうなるでしょうか？

磁石のN極とN極が反発しあうように、斥力(反発力)が働きます。負電荷の近くに負電荷を置いても同じく斥力が働きます。すなわち、

同符号の電荷(プラスとプラス、マイナスとマイナス)間に働く力の向きは斥力が働く方向となります。

一方、正電荷の近くに負電荷を置いた場合はどうなるでしょうか？

磁石のN極とS極が引く付けあうように引力(吸引力)が働きます。すなわち、

異符号の電荷(プラスとマイナス)間に働く力の向きは引力が働く方向となります。

ところで、この力は一体どれくらいの大きさなのでしょうか？それを示した法則がクーロンの法則となっています。

補足

電荷とは、物体が帯びている静電気の量のことを指します。分かりやすく言えば、「電気のかたまり」みたいなものとイメージです。

クーロンの法則の公式

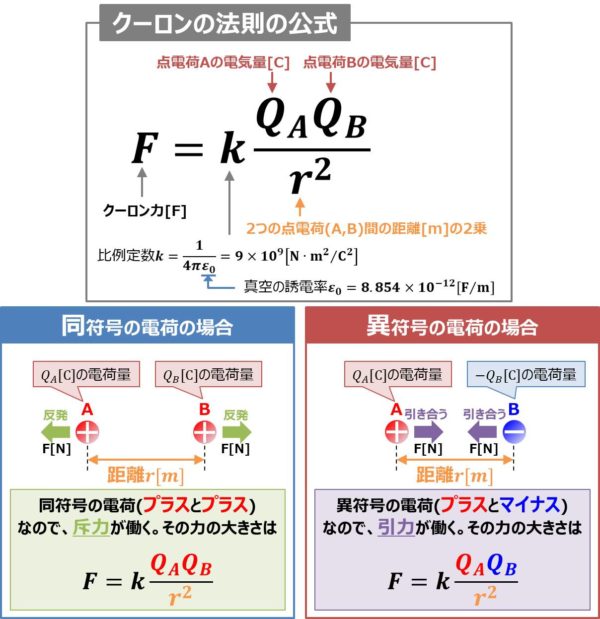
クーロンの法則とは、2つの点電荷(A,B)に働く力は、

2つの点電荷(A,B)の電気量の大きさ(\(Q_{A}{\mathrm{[C]}}\),\(Q_{B}{\mathrm{[C]}}\))の積に比例する。
2つの点電荷(A,B)の距離\(r{\mathrm{[m]}}\)の2乗に反比例する

ことを示した電気磁気学の基本的な法則です。

上記の法則を式で表したものがクーロンの法則の公式であり、次式となっています。

クーロンの法則の公式

\begin{eqnarray}
F=k\frac{Q_{A}Q_{B}}{r^2}
\end{eqnarray}
\(F\)：力の大きさ\({\mathrm{[N]}}\)
\(Q_{A}\)：点電荷Aの電気量の大きさ\({\mathrm{[C]}}\)
\(Q_{B}\)：点電荷Bの電気量の大きさ\({\mathrm{[C]}}\)
\(r\)：2つの点電荷(A,B)間の距離\({\mathrm{[m]}}\)
\(k\)：比例定数で\(k=\displaystyle\frac{1}{4{\pi}{\varepsilon}_{0}}{\;}{\approx}{\;}9×10^{9}{\mathrm{[N{\cdot}m^2/C^2]}}\)という値になります。

この電荷に働く力のことをクーロン力といいます。

2つの点電荷(A,B)が同符号の電荷(プラスとプラス、マイナスとマイナス)の場合は斥力、異符号の電荷(プラスとマイナス)の場合は引力が働きます。また、クーロン力の方向は、2つの点電荷を結ぶ直線状にあります。

補足

点電荷とは、大きさ(面積や体積)を持たない点状の電荷のことを指します。
電荷には大きさ(量)があり、その大きさのことを電気量(または電荷量)といいます。電気量の記号は一般的に「\(Q\)または\(q\)」を使い、単位はクーロン\({\mathrm{[C]}}\)となります。
比例定数\(k\)はクーロン定数と呼ばれています。
クーロン力は、クーロン相互作用、静電力、静電気力、静電引力とも呼ばれています。
クーロンの法則は英語では「Coulomb's law」と書きます。

クーロンの法則の比例定数kについて

クーロンの法則に出てくる\(k\)はクーロン定数と呼ばれる比例定数です。比例定数\(k\)は以下の式で表されます。
\begin{eqnarray}
k=\frac{1}{4{\pi}{\varepsilon}_{0}}
\end{eqnarray}ここで、比例定数\(k\)の式中にある\({\pi}\)は円周率の\({\pi}\)であり「\({\pi}=3.14{\cdots}\)」、\({\varepsilon}_{0}\)は真空の誘電率と呼ばれるものでその値は、
\begin{eqnarray}
{\varepsilon}_{0}=8.854×10^{-12}{\mathrm{[F/m]}}
\end{eqnarray}

となっています。真空の誘電率\({\varepsilon}_{0}\)の単位の中にある\({\mathrm{F}}\)はコンデンサの静電容量(キャパシタンス)の単位を表す『F：ファラド』です。

ここで、円周率の\({\pi}\)と真空の誘電率\({\varepsilon}_{0}\)の値を用いると、

\begin{eqnarray}
k=\frac{1}{4{\pi}{\varepsilon}_{0}}{\;}{\approx}{\;}9×10^{9}{\mathrm{[N{\cdot}m^2/C^2]}}
\end{eqnarray}

となります。この比例定数\(k\)の値は\(k=9×10^{9}{\mathrm{[N{\cdot}m^2/C^2]}}\)で決まっており、クーロンの法則を用いる問題でよく使うので覚えてください。

また、真空の誘電率\({\varepsilon}_{0}\)は空気の誘電率とほぼ同じ(真空の誘電率を1とすると、空気の誘電率は1.00059)なので、クーロンの法則に出てくる比例定数\(k\)は空気中でもほぼ同じ値になります。

補足

誘電率とは『物質の誘電分極のしやすさ』のこと意味します。分かりやすく言えば、『電荷の貯めやすさを示すもの』というイメージです。

クーロンの法則の歴史

クーロンの法則が発見されたのは1785年頃です。

フランスの物理学者シャルル・ド・クーロン(Charles-Augustin de Coulomb)は、微少な力の変化を測定できるねじれ秤(ねじりばかり)を製作しました。

ねじれ秤とは、2つの小球を帯電させて、様々な距離で2つの小球間に働く力を測定する装置です。このねじれ秤を用いて、何度も2つの小球の間に働く力を測定した結果、2つの小球の間に働く力は、

2つの小球の電気量の大きさの積に比例する。
2つの小球の距離の2乗に反比例する

ことを明らかにしました。すなわち、クーロンの法則を発見したのです。

『クーロンの法則』と『万有引力の法則』の違い

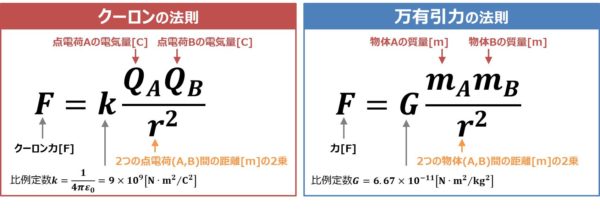
クーロンの法則は万有引力の法則とよく似ています。

万有引力の法則とは、2つの物体(A,B)に働く力は

2つの物体(A,B)の質量(\(m_{A}{\mathrm{[kg]}}\),\(m_{B}{\mathrm{[kg]}}\))の積に比例する。
2つの物体(A,B)の距離の2乗に反比例する。

ことを示した法則です。

上記の法則を式で表したものが万有引力の法則の公式であり、次式となっています。

万有引力の法則の公式

\begin{eqnarray}
F=G\frac{m_{A}m_{B}}{r^2}
\end{eqnarray}
\(F\)：力の大きさ\({\mathrm{[N]}}\)
\(m_{A}\)：物体Aの質量\({\mathrm{[kg]}}\)
\(m_{B}\)：物体Bの質量\({\mathrm{[kg]}}\)
\(r\)：2つの物体(A,B)間の距離\({\mathrm{[m]}}\)
\(G\)：比例定数で\(G=6.67×10^{-11}{\mathrm{[N{\cdot}m^2/kg^2]}}\)という値になります。

この比例定数\(G\)は万有引力定数と呼ばれています。

クーロンの法則と万有引力の法則を並べてみるととてもよく似ていますね。では、違いはどこでしょうか。

それは、電荷にはプラスとマイナスという符号があるということです。万有引力の法則は引力しか働きません。

しかし、クーロンの法則では同符号の電荷(プラスとプラス、マイナスとマイナス)の場合は引力、異符号の電荷(プラスとマイナス)の場合は斥力が働きます。