『ミラー効果』と『ミラー容量』とは？

この記事では『ミラー効果』と『ミラー容量』について

『ミラー効果』と『ミラー容量』とは
『ミラー効果』と『ミラー容量』の式の導出方法

などを図を用いて分かりやすく説明しています。

『ミラー効果』と『ミラー容量』とは？

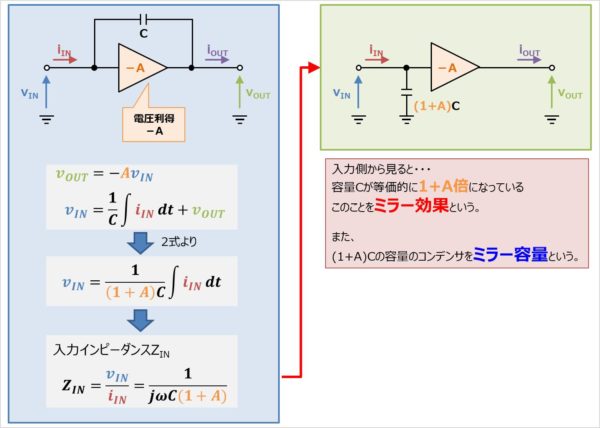
上図の左に示すように、電圧利得-A倍の増幅器の入力と出力の間に容量Cが存在する場合を考えます。

この時、入力インピーダンスZ_INは
\begin{eqnarray}
Z_{IN}=\frac{ v_{IN}}{ i_{IN}} =\frac{1}{j{\omega} (1+A)C}
\end{eqnarray}
となります。

これは入力側から見ると、容量Cが等価的に1+A倍になっているように見えます。このことをミラー効果といい、大きく見える容量のことをミラー容量といいます。

では次に、上記の式の導出方法について説明します。

補足

ミラー効果(Miller Effect)は，1920年にJohn Milton Miller氏によって発表された現象です。ミラー効果のミラーは発見した人の名前が由来となっています。

『ミラー効果』と『ミラー容量』の式の導出方法

増幅器の入出力インピーダンスが理想的であるとし、入力インピーダンスは無限大とします。

この時、出力電圧v_OUTと入力電圧v_INは以下の2式で表されます。
\begin{eqnarray}
v_{OUT}&=-&Av_{IN}\\
v_{IN}&=&\frac{1}{C}\int i_{IN}dt+ v_{OUT}
\end{eqnarray}
2式より入力電圧v_INは以下の式となります。
\begin{eqnarray}
v_{IN}=\frac{1}{(1+A)C}\int i_{IN}dt
\end{eqnarray}
ここで、上式をラプラス変換すると、以下の式となります。
\begin{eqnarray}
v_{IN}(s)=\frac{1}{s(1+A)C} i_{IN}
\end{eqnarray}
その後、フーリエ変換を行い、sをjωに変換すると、入力インピーダンスZ_INは以下の式となります。
\begin{eqnarray}
Z_{IN}=\frac{ v_{IN}}{ i_{IN}} =\frac{1}{j{\omega} (1+A)C}
\end{eqnarray}
つまり、上図の左の回路を入力側から見ると、(1+A)Cの容量のコンデンサが並列に接続されている状態と等価となります。そのため、上図の右の等価回路に置き換えが可能となります。