LTspiceで表示波形の平均値と実行値を表示する方法について説明します。
平均値と実行値の表示方法
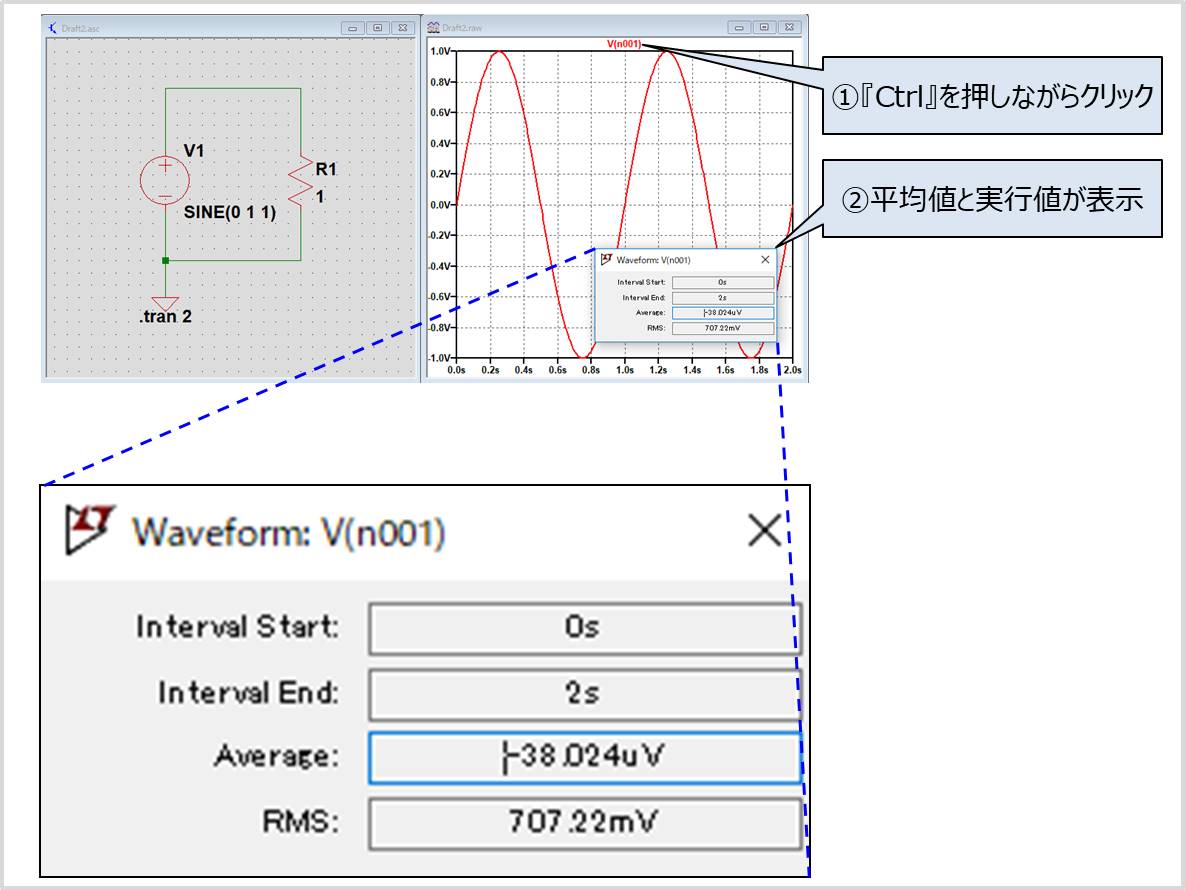
LTspiceにおいて、シミュレーション実行後、表示波形の平均値と実行値を表示方法は、
- 表示波形の上にある文字をCtrlを押しながらクリックする。
- 平均値(Average)と実行値(RMS)が表示される。
となっています。
上図では、周期T=1[s]、振幅VM=1[V]の正弦波v(t)の電圧波形を表示しています。
実行値VRMSは707mV(=0.707V)、平均値VAVEは-38uV(ほぼ0V)となっています。
ここで、シミュレーション結果と計算結果を比較してみます。
振幅VM=1[V]の正弦波v(t)の実行値VRMSは、
\begin{eqnarray}
V_{RMS} &=& \displaystyle\frac{V_M}{\sqrt{2}}=0.707[V]
\end{eqnarray}
となります。
これより、シミュレーション結果と計算結果が等しいことが分かります。
また、振幅VM=1[V]の正弦波v(t)の平均値VAVEは
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{2V_M}{\pi}=0.637[V]
\end{eqnarray}
となります。
これより、シミュレーション結果と計算結果が異なっていることが分かります。
異なる理由をこれから説明します。
なお、正弦波の実行値と平均値の詳しい計算方法について以下の記事に記載しているので参照してください。
『正弦波』の実効値・平均値・波形率・波高率の求め方
シミュレーション結果と計算結果が異なる理由
計算で波形v(t)の平均値VAVEを求める場合、v(t)の絶対値|v(t)|を使用します。
周期をTとすると、計算における波形v(t)の平均値VAVEは、
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}|v(t)|dt
\end{eqnarray}
となります。
一方、LTspiceでの平均値は波形v(t)の絶対値|v(t)|を取らず、v(t)を使用します。
周期をTとすると、LTspiceにおける波形v(t)の平均値VAVEは、
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}v(t)dt
\end{eqnarray}
となります。
このように『絶対値を取る計算』と、『絶対値を取らないLTspiceでの内部計算』の計算方法の血がいによって、シミュレーション結果と計算結果で差異が生じています。
表示波形の範囲を変えると平均値と実行値が変わるので注意
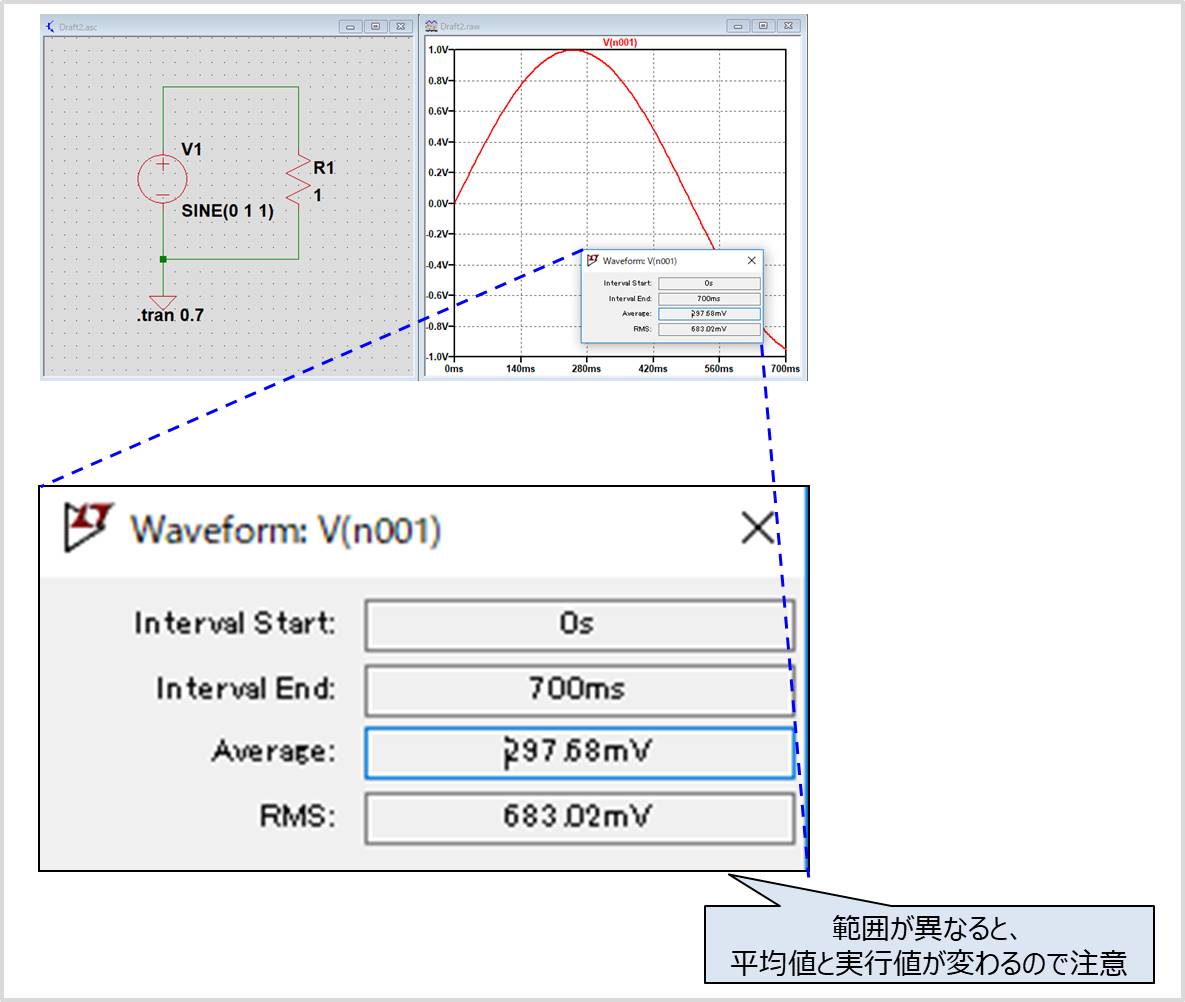
例えば、周期1[s]の正弦波に対して、「.tran 1」から「.tran 0.7」に変更し、0.7[s]の期間だけを表示したのが上図です。
シミュレーション結果を見ると、実行値VRMSが683mVとなっており、先ほど示した「.tran 1」における実行値VRMS(707mV)と値が異なることが分かります。






