この記事では『電源が供給できる最大電力(最大供給電力)』について
- 電源が供給できる最大電力(最大供給電力)の『公式』と『計算方法』
- 定電圧源が供給できる最大電力(最大供給電力)
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
最大電力(最大供給電力)の公式
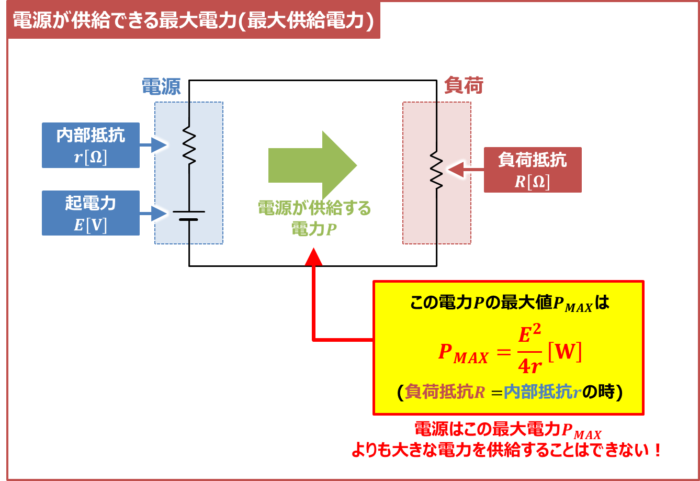
内部抵抗が\(r{\mathrm{[{\Omega}]}}\)で起電力が\(E{\mathrm{[V]}}\)の電源に負荷抵抗\(R{\mathrm{[{\Omega}]}}\)を接続した時、負荷抵抗\(R\)で消費される電力(電源が供給する電力)\(P\)は、負荷抵抗\(R\)と内部抵抗\(r\)が等しい時(\(R=r\)の時)に最大値\(P_{MAX}\)になり、最大電力\(P_{MAX}\)は次式で表されます。
\begin{eqnarray}
P_{MAX}=\frac{E^2}{4r}{\mathrm{[W]}}\tag{1}
\end{eqnarray}
電源はこの最大電力\(P_{MAX}\)よりも大きな電力を供給することはできません。すなわち、言い換えれば、内部抵抗を持つ電源は供給できる電力には限界があるということです。
では次に、
- 「\(R=r\)の時」に電源が供給する電力が最大値\(P_{MAX}\)になる理由
- 「電源が供給できる最大電力\(P_{MAX}=\displaystyle\frac{E^2}{4r}\)」の導出方法と計算方法
について説明します。
補足
- 「負荷抵抗\(R\)=内部抵抗\(r\)」の条件は「最大電力の条件」と呼ばれています。
最大電力(最大供給電力)の計算方法・導出方法
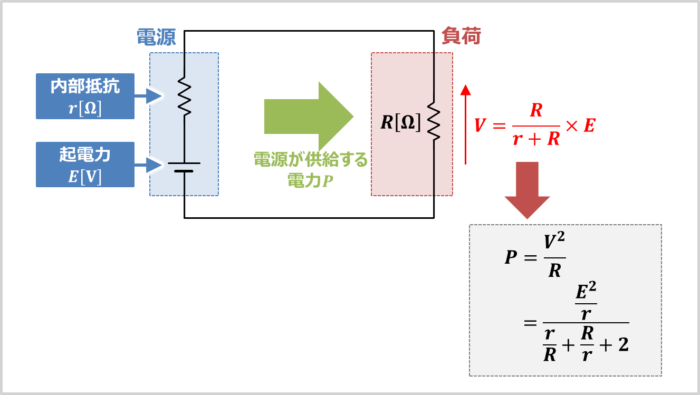
上図に示しているのは、内部抵抗が\(r{\mathrm{[{\Omega}]}}\)で起電力が\(E{\mathrm{[V]}}\)の電源に負荷抵抗\(R{\mathrm{[{\Omega}]}}\)を接続している回路です。この回路において、負荷抵抗\(R\)にかかる電圧を\(V{\mathrm{[V]}}\)とします。
分圧の法則より、負荷抵抗\(R\)にかかる電圧\(V\)は次式となります。
\begin{eqnarray}
V=\frac{R}{r+R}×E{\;}{\mathrm{[V]}}\tag{2}
\end{eqnarray}
したがって、負荷抵抗\(R\)で消費される電力(電源が供給する電力)\(P\)は次式となります。
\begin{eqnarray}
P&=&\frac{V^2}{R}\\
\\
&=&\frac{\left(\displaystyle\frac{R}{r+R}×E\right)^2}{R}\\
\\
&=&\frac{RE^2}{(r+R)^2}\\
\\
&=&\frac{RE^2}{r^2+2rR+R^2}\\
\\
&=&\frac{E^2}{\displaystyle\frac{r^2}{R}+2r+R}\\
\\
&=&\frac{\displaystyle\frac{E^2}{r}}{\displaystyle\frac{r}{R}+2+\displaystyle\frac{R}{r}}\\
\\
&=&\frac{\displaystyle\frac{E^2}{r}}{\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}+2}{\mathrm{[W]}}\tag{3}
\end{eqnarray}
では次に、負荷抵抗\(R\)で消費される電力(電源が供給する電力)\(P\)の最大値\(P_{MAX}\)を求めます。
(3)式の分子「\(\displaystyle\frac{E^2}{r}\)」は定数なので、(3)式の分母「\(\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}+2\)」が最小になる時に、電源が供給する電力\(P\)が最大値\(P_{MAX}\)になります。
ここで、「相加・相乗平均の関係」から、次式が成り立ちます。
相加・相乗平均の関係
\begin{eqnarray}
\frac{\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}}{2}&{\;}{≥}{\;}&\sqrt{\displaystyle\frac{r}{R}×\displaystyle\frac{R}{r}}\\
\\
{\Leftrightarrow}\frac{r}{R}+\frac{R}{r}&{\;}{≥}{\;}&2\sqrt{\displaystyle\frac{r}{R}×\displaystyle\frac{R}{r}}\\
\\
&{\;}{≥}{\;}&2\sqrt{1}\\
\\
&{\;}{≥}{\;}&2\tag{4}
\end{eqnarray}
したがって、分母にある「\(\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}\)」は2以上になります。言い換えれば、「\(\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}\)」が最小値の「2」になるとき、(3)式の分母「\(\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}+2\)」が最小になるということです。
ここで、等号条件が成立する条件(\(\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}=2\)になる条件)は「\(\displaystyle\frac{r}{R}=\displaystyle\frac{R}{r}\)」の時であり、
\begin{eqnarray}
\frac{r}{R}&=&\frac{R}{r}\\
\\
{\Leftrightarrow}R&=&r\tag{5}
\end{eqnarray}
となります。すなわち、負荷抵抗\(R\)と内部抵抗\(r\)が等しい時(\(R\)=\(r\)の時)に、(3)式の分母「\(\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}+2\)」が最小となり、電源が供給する電力\(P\)が最大値\(P_{MAX}\)になります。
(5)式を(3)式に代入すると、次式のようになり、電源が供給できる最大電力(最大供給電力)\(P_{MAX}\)を導出することができます。
\begin{eqnarray}
P_{MAX}&=&\frac{\displaystyle\frac{E^2}{r}}{\displaystyle\frac{r}{r}+\displaystyle\frac{r}{r}+2}\\
\\
&=&\frac{E^2}{4r}{\mathrm{[W]}}\tag{6}
\end{eqnarray}
あわせて読みたい
『分圧の法則』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る
【分圧の法則とは】直列接続された抵抗にかかる電圧について
補足
- 負荷抵抗\(R\)を電源の内部抵抗\(r\)と等しくなるように調整することを『整合をとる』といいます。
電源が供給する電力のグラフ
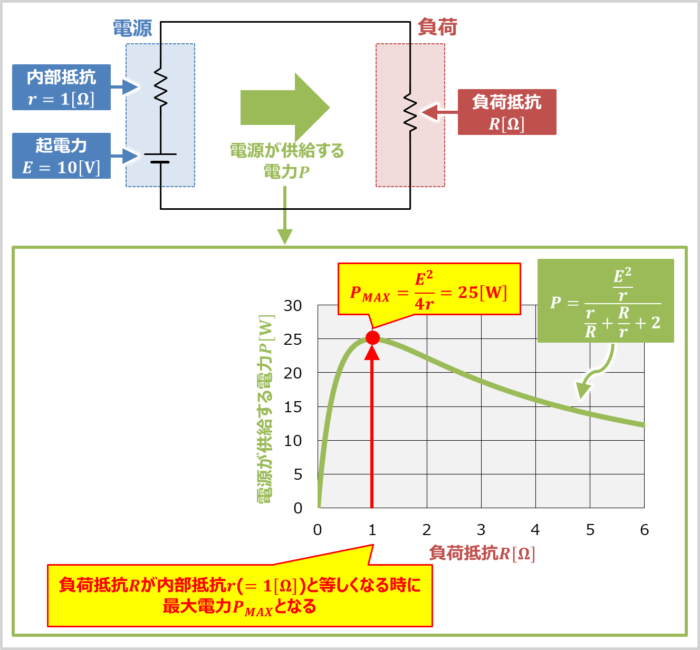

上図に示しているのは、内部抵抗が\(r{\mathrm{[{\Omega}]}}\)で起電力が\(E{\mathrm{[V]}}\)の電源に負荷抵抗\(R{\mathrm{[{\Omega}]}}\)を接続している回路です。この回路において、負荷抵抗\(R\)で消費される電力(電源が供給する電力)\(P\)は次式となります。
\begin{eqnarray}
P=\frac{\displaystyle\frac{E^2}{r}}{\displaystyle\frac{r}{R}+\displaystyle\frac{R}{r}+2}{\mathrm{[W]}}\tag{7}
\end{eqnarray}
(7)式は(3)式と同じです。
(7)式をグラフで描いてみましょう。一例として、電源の起電力\(E\)を10V、電源の内部抵抗\(r\)を1Ωとした時において、負荷抵抗\(R\)を変化させた時の電源が供給する電力\(P\)を上図に示しています。
この場合、電源が供給できる最大電力(最大供給電力)\(P_{MAX}\)は(1)式より次式となります。
\begin{eqnarray}
P_{MAX}=\frac{E^2}{4r}=\frac{10^2}{4×1}=25{\mathrm{[W]}}\tag{8}
\end{eqnarray}
グラフを見ても、負荷抵抗\(R\)が内部抵抗\(r\)(\(=1{\mathrm{[{\Omega}]}}\))と等しくなる時に、電源が供給する電力\(P\)が最大値\(P_{MAX}=25{\mathrm{[W]}}\)になっていることが分かります。
定電圧源が供給できる最大電力(最大供給電力)
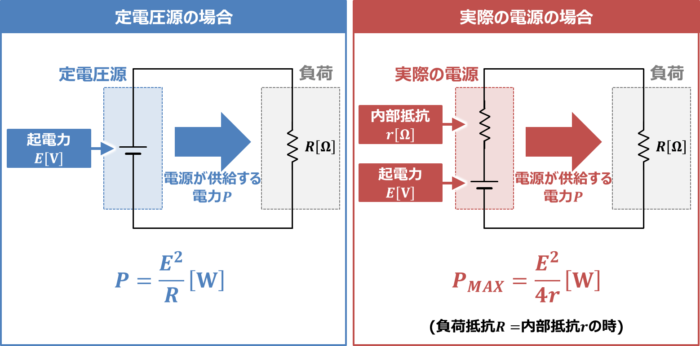

内部抵抗\(r\)が0Ωの定電圧源の場合、定電圧源の起電力を\(E{\mathrm{[V]}}\)とすると、負荷抵抗\(R\)で消費される電力(電源が供給する電力)\(P\)は次式になります。
\begin{eqnarray}
P=\frac{E^2}{R}{\mathrm{[W]}}\tag{9}
\end{eqnarray}
したがって、負荷抵抗\(R\)が小さければ小さいほど、電源が供給する電力\(P\)が大きくなります。すなわち、定電圧源の場合はいくらでも負荷に電力を供給することができます。
しかし、実際には、電源は内部抵抗\(r{\mathrm{[{\Omega}]}}\)を持っているため、電源が供給できる電力には限界があり、電源が供給できる最大電力(最大供給電力)\(P_{MAX}\)は次式となります。
\begin{eqnarray}
P_{MAX}=\frac{E^2}{4r}{\mathrm{[W]}}\tag{10}
\end{eqnarray}
まとめ
この記事では『電源が供給できる最大電力(最大供給電力)』について、以下の内容を説明しました。
- 電源が供給できる最大電力(最大供給電力)の『公式』と『計算方法』
- 定電圧源が供給できる最大電力(最大供給電力)
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






