【インダクタの直並列接続】インダクタンスの『計算』と『例題』について！

この記事では『インダクタの直並列接続』について

直並列接続されたインダクタの合成インダクタンスの『計算方法』・『例題』

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

インダクタの直並列接続

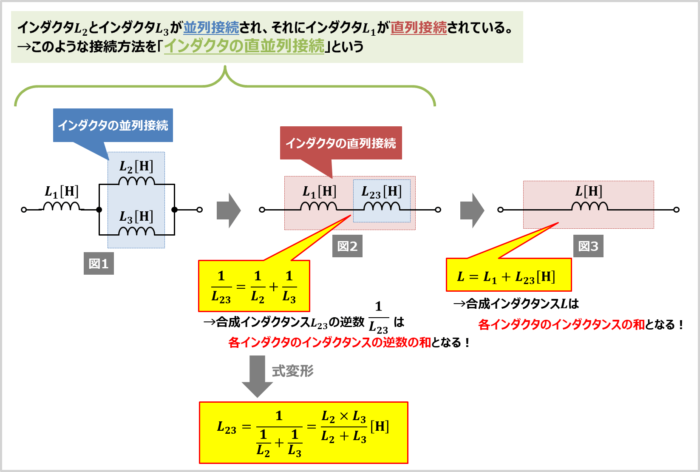
図1に示す回路は、インダクタ\(L_2\)とインダクタ\(L_3\)が並列接続され、それにインダクタ\(L_1\)が直列接続されています。このような接続方法を「インダクタの直並列接続」といいます。

ポイント

『直列接続』と『並列接続』を組み合わせた接続方法が『直並列接続』です。

上図に示しているような直並列接続されたインダクタの場合、合成インダクタンス\(L\)は以下の手順(ステップ1,2)で求めることができます。

合成インダクタンスLを求める手順

並列接続されているインダクタ\(L_2\)と\(L_3\)の合成インダクタンス\(L_{23}\)を求める。
インダクタ\(L_1\)と\(L_{23}\)の合成インダクタンス\(L\)を求める。

ステップ1

まず、並列接続されている「インダクタンスが\(L_2{\mathrm{[H]}}\)のインダクタ」と「インダクタンスが\(L_3{\mathrm{[H]}}\)のインダクタ」の合成インダクタンス\(L_{23}{\mathrm{[H]}}\)を求めます。

並列接続されたインダクタの場合、合成インダクタンス\(L_{23}\)の逆数\(\displaystyle\frac{1}{L_{23}}\)は各インダクタのインダクタンスの逆数の和で計算することができ、次式で表されます。

\begin{eqnarray}
\frac{1}{L_{23}}=\frac{1}{L_2}+\frac{1}{L_3}\tag{1}
\end{eqnarray}

(1)式を変形すると、合成インダクタンス\(L_{23}\)は次式で表されます。

\begin{eqnarray}
L_{23}=\frac{1}{\displaystyle\frac{1}{L_2}+\displaystyle\frac{1}{L_3}}=\frac{L_2×L_3}{L_2+L_3}{\mathrm{[H]}}\tag{2}
\end{eqnarray}

並列接続されている「インダクタンスが\(L_2{\mathrm{[H]}}\)のインダクタ」と「インダクタンスが\(L_3{\mathrm{[H]}}\)のインダクタ」は「インダクタンス\(L_{23}{\mathrm{[H]}}\)の1つのインダクタ」と見なせるので、図2のように変形することができます。このように変形すると、インダクタ\(L_1\)と\(L_{23}\)が直列接続されているようになります。

ステップ2

次に、直列接続されている「インダクタンスが\(L_1{\mathrm{[H]}}\)のインダクタ」と「インダクタンスが\(L_{23}{\mathrm{[H]}}\)のインダクタ」の合成インダクタンス\(L{\mathrm{[H]}}\)を求めます。

直列接続されたインダクタの場合、合成インダクタンス\(L\)は各インダクタのインダクタンスの和で計算することができ、次式で表されます。

\begin{eqnarray}
L=L_1+L_{23}=L_1+\frac{L_2×L_3}{L_2+L_3}{\mathrm{[H]}}\tag{3}
\end{eqnarray}

合成インダクタンスとは

複数のインダクタをまとめて1つのインダクタとした時のインダクタンスを合成インダクタンスと呼びます。

インダクタの直並列接続の例題

例題

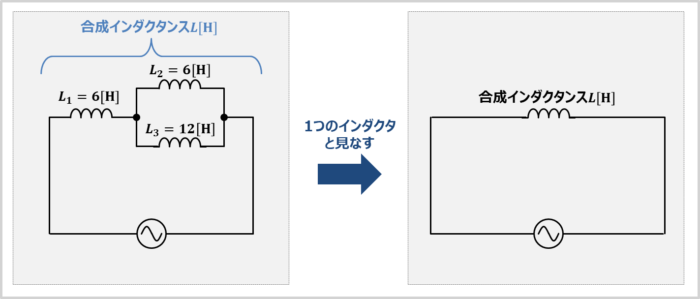
上図に示した回路において、インダクタ\(L_1\)が\(6{\mathrm{[H]}}\)、インダクタ\(L_2\)が\(6{\mathrm{[H]}}\)、インダクタ\(L_3\)が\(12{\mathrm{[H]}}\)の時、インダクタ\(L_1\)～\(L_3\)の合成インダクタンス\(L\)は何\({\mathrm{H}}\)でしょうか。

解答

インダクタ\(L_2\)と\(L_3\)は並列接続されているので、並列接続されたインダクタの場合、合成インダクタンス\(L_{23}\)の逆数\(\displaystyle\frac{1}{L_{23}}\)は各インダクタのインダクタンスの逆数の和で計算することができ、以下の値となります。

\begin{eqnarray}
\frac{1}{L_{23}}=\frac{1}{L_2}+\frac{1}{L_3}\tag{4}
\end{eqnarray}

したがって、(4)式を変形すると、合成インダクタンス\(L_{23}\)は以下の値となります。

\begin{eqnarray}
L_{23}&=&\frac{1}{\displaystyle\frac{1}{L_2}+\displaystyle\frac{1}{L_3}}\\
\\
&=&\frac{L_2×L_3}{L_2+L_3}\\
\\
&=&\frac{6×12}{6+12}\\
\\
&=&4{\mathrm{[H]}}\tag{5}
\end{eqnarray}

インダクタ\(L_1\)と\(L_{23}\)は直接接続されているので、合成インダクタンス\(L\)は各インダクタのインダクタンスの和で計算することができ、以下の値となります。

\begin{eqnarray}
L=L_1+L_{23}=6+4=10{\mathrm{[H]}}\tag{6}
\end{eqnarray}