この記事では『コンデンサの並列接続』について
- 並列接続されたコンデンサの合成静電容量の『計算方法』・『証明』・『例題』
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
【コンデンサの並列接続】静電容量の『計算』
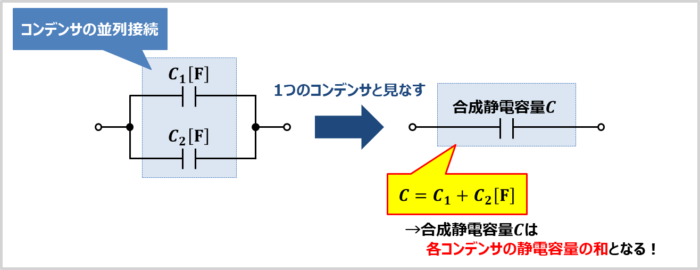
コンデンサ\(C_1\)とコンデンサ\(C_2\)を並列に接続することを「コンデンサの並列接続」といいます。
「静電容量が\(C_1{\mathrm{[F]}}\)のコンデンサ」と「静電容量が\(C_2{\mathrm{[F]}}\)のコンデンサ」が並列接続されている時、合成静電容量\(C\)は各コンデンサの静電容量の和で計算することができ、次式で表されます。
\begin{eqnarray}
C=C_1+C_2{\mathrm{[F]}}\tag{1}
\end{eqnarray}
合成静電容量とは?
複数のコンデンサをまとめて1つのコンデンサとした時の静電容量を合成静電容量と呼びます。
合成静電容量は「合成容量」や「合成コンデンサの静電容量」などとも呼ばれています。
Nつのコンデンサが並列接続されている時
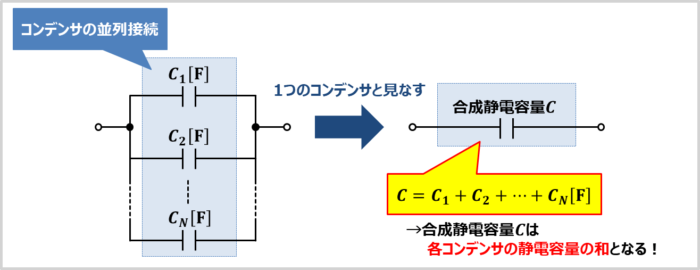
(1)式はコンデンサが3つ以上並列接続されている時にも成り立ちます。
上図に示しているのは、Nつのコンデンサ(各コンデンサの静電容量を\(C_1{\mathrm{[F]}}\),\(C_2{\mathrm{[F]}}\),・・・,\(C_N{\mathrm{[F]}}\)とする)が並列接続されている回路です。
この回路においても、合成静電容量\(C\)は各コンデンサの静電容量の和で計算することができ、次式で表されます。
\begin{eqnarray}
C=C_1+C_2+{\cdots}+C_N{\mathrm{[F]}}\tag{2}
\end{eqnarray}
例えば、3つのコンデンサ(各コンデンサの静電容量を\(C_1{\mathrm{[F]}}\),\(C_2{\mathrm{[F]}}\),\(C_3{\mathrm{[F]}}\)とする)が並列接続されている時の合成静電容量\(C\)は次式となります。
\begin{eqnarray}
C=C_1+C_2+C_3{\mathrm{[F]}}\tag{3}
\end{eqnarray}
【コンデンサの並列接続】静電容量の『証明』
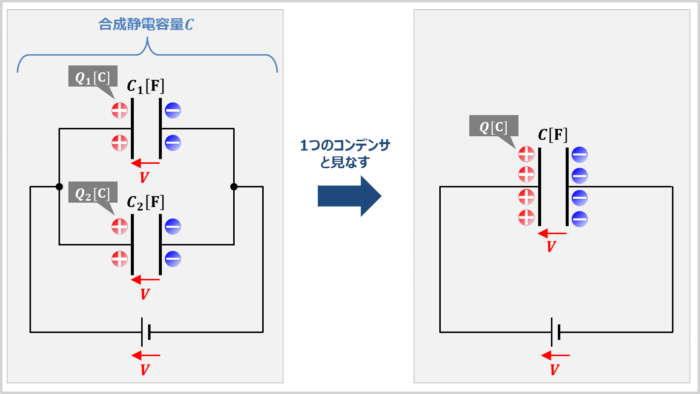
上図に示すように、「静電容量が\(C_1{\mathrm{[F]}}\)のコンデンサ」と「静電容量が\(C_2{\mathrm{[F]}}\)のコンデンサ」を並列接続した後、電源電圧\(V{\mathrm{[V]}}\)を印加して、2つのコンデンサを充電します。
この時、各コンデンサに蓄えられている電荷が下記であるとします。
- コンデンサ\(C_1\)に蓄えられている電荷:\(Q_1{\mathrm{[C]}}\)
- コンデンサ\(C_2\)に蓄えられている電荷:\(Q_2{\mathrm{[C]}}\)
各コンデンサにかかる電圧は電源電圧\(V{\mathrm{[V]}}\)と等しいので、各コンデンサに蓄えられている電荷は「\(Q=CV\)」の公式より次式で表されます。
- コンデンサ\(C_1\)に蓄えられている電荷\(Q_1\)
\begin{eqnarray}
Q_1&=&C_1V\tag{4}
\end{eqnarray}
- コンデンサ\(C_2\)に蓄えられている電荷\(Q_2\)
\begin{eqnarray}
Q_2&=&C_2V\tag{5}
\end{eqnarray}
ポイント
コンデンサを並列接続した場合、静電容量の大きさに関わらず、各コンデンサにかかる電圧が同じとなります。
ここで、2つのコンデンサに蓄えられている電荷の合計を\(Q{\mathrm{[C]}}\)とすると、次式が成り立ちます。
\begin{eqnarray}
Q=Q_1+Q_2\tag{6}
\end{eqnarray}
2つのコンデンサの合成静電容量を\(C{\mathrm{[F]}}\)とすると、2つのコンデンサに蓄えられている電荷の合計が\(Q{\mathrm{[C]}}\)なので、次式が成り立ちます。
\begin{eqnarray}
Q=CV\tag{7}
\end{eqnarray}
(6)式に(4)式と(5)式を(7)式に代入すると、次式のようになり、合成静電容量\(C\)は各コンデンサの静電容量の和で計算できることが分かります。
\begin{eqnarray}
Q=Q_1+Q_2\\
\\
CV=C_1V+C_2V\\
\\
C=C_1+C_2{\mathrm{[F]}}\tag{8}
\end{eqnarray}
【コンデンサの並列接続】静電容量を求める例題
例題
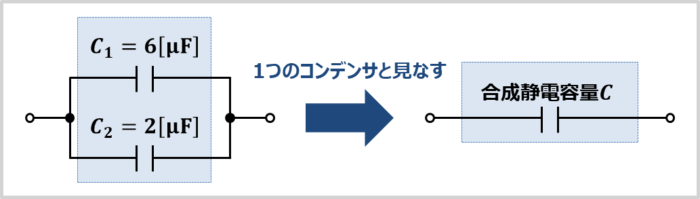
上図に示した回路において、コンデンサ\(C_1\)が\(6{\mathrm{[μF]}}\)、コンデンサ\(C_2\)が\(2{\mathrm{[μF]}}\)の時、コンデンサ\(C_1\)と\(C_2\)の合成静電容量\(C\)は何\({\mathrm{F}}\)でしょうか。
解答
各コンデンサの静電容量は「\(C_1=6{\mathrm{[μF]}}\)」と「\(C_2=2{\mathrm{[μF]}}\)」となっているので、まず単位を\({\mathrm{[μF]}}\)から\({\mathrm{[F]}}\)に変換します。
「\({\mathrm{μ}}\)(マイクロ)」は「\(10^{-6}\)」を表しているので、単位変換すると各コンデンサの静電容量は下記となります。
\begin{eqnarray}
C_1&=&6{\mathrm{[μF]}}=6×10^{-6}{\mathrm{[F]}}\tag{9}\\
\\
C_2&=&2{\mathrm{[μF]}}=2×10^{-6}{\mathrm{[F]}}\tag{10}
\end{eqnarray}
(9)式と(10)式を(1)式に代入すると、コンデンサ\(C_1\)と\(C_2\)の合成静電容量\(C\)を求めることができ、下記の値となります。
\begin{eqnarray}
C=C_1+C_2=6×10^{-6}+2×10^{-6}=8×10^{-6}{\mathrm{[F]}}\tag{11}
\end{eqnarray}
あわせて読みたい
「\({\mathrm{μF}}\)(マイクロファラド)」の「\({\mathrm{μ}}\)(マイクロ)」は「\(10^{-6}\)」を表しています。
「\({\mathrm{μ}}\)(マイクロ)」はSI接頭語(大きな桁や小さな桁を表すために、単位の前に付けられている接頭語)です。その他には距離を表す単位の「\({\mathrm{mm}}\)(ミリメートル)」の「\({\mathrm{m}}\)(ミリ)」、「\({\mathrm{cm}}\)(センチメートル)」の「\({\mathrm{c}}\)(センチ)」、「\({\mathrm{km}}\)(キロメートル)」の「\({\mathrm{k}}\)(キロ)」などがSI接頭語となります。
SI接頭語については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-

SI接頭語とは?『覚え方』や『一覧表』を解説!
続きを見る
コンデンサを並列接続すると合成静電容量が大きくなる理由

コンデンサの並列接続についてもう少し深堀してみましょう。
コンデンサを並列接続した場合、合成静電容量\(C\)は各コンデンサの静電容量よりも大きくなります。これはなぜででしょうか。
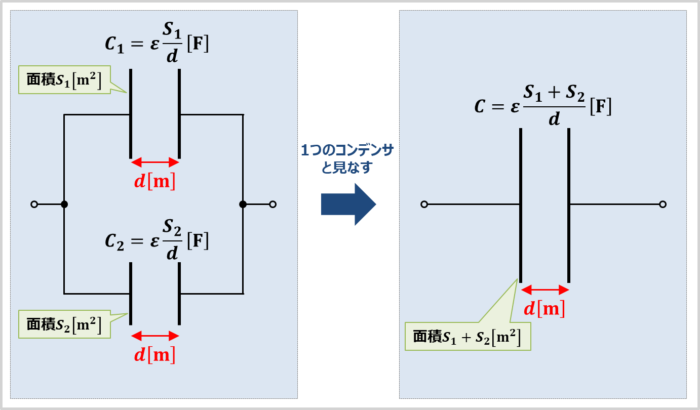
面積\(S{\mathrm{[m^2]}}\)の2つの電極板の距離\(d{\mathrm{[m]}}\)離して平行においたコンデンサの静電容量\(C{\mathrm{[F]}}\)は面積\(S\)に比例し、距離\(d\)に反比例します。ここで誘電率を\({\varepsilon}\)とすると、コンデンサの静電容量\(C\)は次式で表されます。
\begin{eqnarray}
C={\varepsilon}\frac{S}{d}{\mathrm{[F]}}\tag{12}
\end{eqnarray}
また、コンデンサ\(C_1\)の電極板の面積を\(S_1{\mathrm{[m^2]}}\)、コンデンサ\(C_2\)の電極板の面積を\(S_2{\mathrm{[m^2]}}\)とすると、コンデンサ\(C_1\)と\(C_2\)の静電容量は次式で表されます(各コンデンサの誘電率\({\varepsilon}\)と電極板の距離\(d\)が等しいとします)。
\begin{eqnarray}
C_1&=&{\varepsilon}\frac{S_1}{d}{\mathrm{[F]}}\tag{13}\\
\\
C_1&=&{\varepsilon}\frac{S_2}{d}{\mathrm{[F]}}\tag{14}
\end{eqnarray}
(13)式と(14)式を(1)式に代入すると次式となります。
\begin{eqnarray}
C=C_1+C_2={\varepsilon}\frac{S_1}{d}+{\varepsilon}\frac{S_1}{d}={\varepsilon}\frac{S_1+S_2}{d}{\mathrm{[F]}}\tag{15}
\end{eqnarray}
上式より、コンデンサ\(C_1\)と\(C_2\)の誘電率\({\varepsilon}\)と電極板の距離\(d\)が同じ場合、コンデンサを並列接続すると、合成静電容量\(C\)は電極板の面積\(S\)が広くなった(\(S_1+S_2\))のと等価になります。電極板の面積\(S\)が広くなれば、(12)式より静電容量\(C\)が大きくなることはイメージできると思います。
あわせて読みたい
誘電率\({\varepsilon}\)については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-


【誘電率とは?】比誘電率や単位などを分かりやすく説明します!
続きを見る
まとめ
この記事では、『コンデンサの並列接続』について、以下の内容を説明しました。
- 並列接続されたコンデンサの合成静電容量の『計算方法』・『証明』・『例題』
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。







