この記事では『表皮効果』について
- 表皮効果とは
- 表皮効果の『原理』・『計算式』・『対策』
- 表皮深さとは
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
表皮効果とは
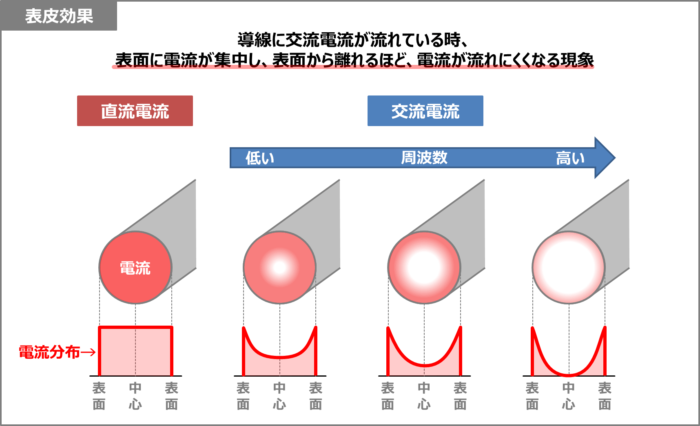
表皮効果とは、導線に交流電流が流れている時、導線の表面に電流が集中し、導線の表面から離れるほど(導線の中心部に近づくほど)、電流が流れにくくなる現象です。
交流電流の周波数が高くなるほど、導線の中心部に流れる電流が減少し、電流の流れる面積が小さくなるため、導線の抵抗値が高くなります。
補足
- 表皮効果は1867年にウィリアム・トムソン(ケルヴィン卿)によって発見されました。
- 表皮効果は英語では「Skin Effect」と書きます。
表皮効果の原理
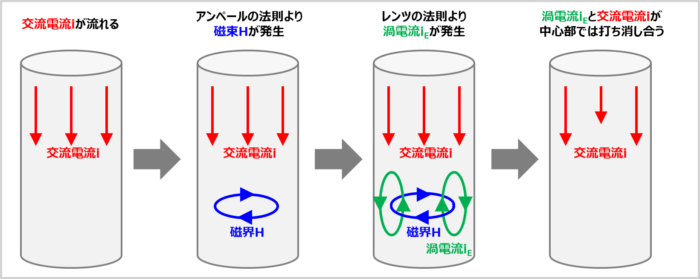
表皮効果の原理は「アンペールの法則」と「レンツの法則」を用いて説明することができます。
交流電流\(i\)はプラスとマイナスが交互に変化する電流です。上図に示しているのは、導線に交流電流\(i\)が流れている時(交流電流\(i\)がプラスになって流れ始めた時)の磁界\(H\)と渦電流\(i_E\)の様子を示しています。
交流電流\(i\)が流れ始めた時、交流電流\(i\)の周囲には「アンペールの法則」より磁界\(H\)が発生します。磁界\(H\)の向きは右手の法則(右ねじの法則)によって決まります。
磁界\(H\)が発生すると、「レンツの法則」より、その磁界\(H\)の変化を妨げる方向に渦電流\(i_E\)が発生します。渦電流\(i_E\)の向きも右手の法則(右ねじの法則)によって決まります。
渦電流\(i_E\)と交流電流\(i\)の向きを比較すると、導線の中心部では反対の向きになっています。すなわち、導線の中心部では、渦電流\(i_E\)が交流電流\(i\)を打ち消しているということです。そのため、導線に交流電流\(i\)が流れている時、導線の中心部に近づくほど、電流が流れにくくなります。
また、交流電流\(i\)の周波数が高いほど、磁界\(H\)の変化が激しくなるため、渦電流\(i_E\)が増加し、交流電流\(i\)を打ち消す度合いが大きくなります。そのため、交流電流\(i\)の周波数が高いほど、導線の中心部に流れる電流が減少します。
あわせて読みたい
「アンペールの法則」と「レンツの法則」と「右手の法則」については、それぞれ下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-

【アンペールの法則とは?】積分形と微分形の式と導出方法について!
続きを見る
-


【レンツの法則とは】起電力の向きについてわかりやすく解説!
続きを見る
-


右ねじの法則(右手の法則)とは?わかりやすく解説!
続きを見る
表皮効果の式(表皮深さとは?)
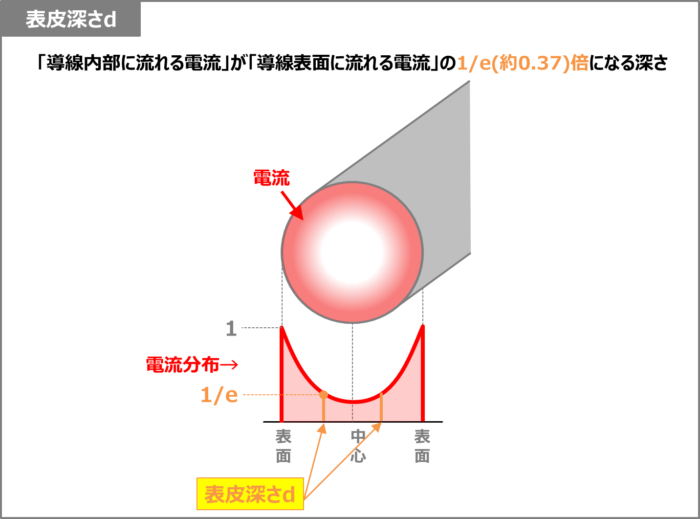

表皮効果によって、導線の表面から離れるほど電流が流れにくくなることを説明しました。
では一体、導線の表面からどの程度の位置まで電流が流れるのでしょうか。それを定量的に表すために「表皮深さ\(d\)」というものがあります。
表皮深さ\(d\)は「導線内部に流れる電流」が「導線表面に流れる電流」の1/e(約0.37)倍になる深さであり、次式で表されます。
\begin{eqnarray}
d=\displaystyle\sqrt{\displaystyle\frac{2{\rho}}{{\omega}{\mu}}}=\displaystyle\sqrt{\displaystyle\frac{2}{{\omega}{\mu}{\sigma}}}=\displaystyle\sqrt{\displaystyle\frac{1}{{\pi}f{\mu}{\sigma}}}
\end{eqnarray}
\begin{eqnarray}
\\
d&:&表皮深さ{\mathrm{[m]}}\\
{\rho}&:&導体の電気抵抗率{\mathrm{[{\Omega}{\cdot}m]}}=1/{\sigma}\\
{\omega}&:&交流電流の角周波数{\mathrm{[rad/s]}}=2{\pi}f\\
{\mu}&:&導体の透磁率{\mathrm{[H/m]}}\\
{\sigma}&:&導体の導電率{\mathrm{[S/m]}}\\
f&:&交流電流の周波数{\mathrm{[Hz]}}\\
\end{eqnarray}
ここで、導線が銅の場合における表皮深さ\(d\)を計算してみましょう。
銅は反磁性体(非磁性体)なので、銅の透磁率\({\mu}\)は真空の透磁率\({\mu}_0(=4{\pi}×10^{-7}{\mathrm{[H/m]}})\)とほぼ等しくなり、以下の値となります。
\begin{eqnarray}
{\mu}{\;}{\approx}{\;}{\mu}_0=4{\pi}×10^{-7}{\mathrm{[H/m]}}
\end{eqnarray}
また、銅の導電率\({\sigma}\)は20℃環境においては、以下の値となります。
\begin{eqnarray}
{\sigma}=5.96×10^{7}{\mathrm{[S/m]}}
\end{eqnarray}
したがって、銅の表皮深さ\(d\)は次式で表されます。
\begin{eqnarray}
d{\;}{\approx}{\;}0.065\displaystyle\sqrt{\displaystyle\frac{1}{f}}{\mathrm{[m]}}
\end{eqnarray}
ここで、下図に周波数\(f\)を変化させた時の表皮深さ\(d\)を示します。
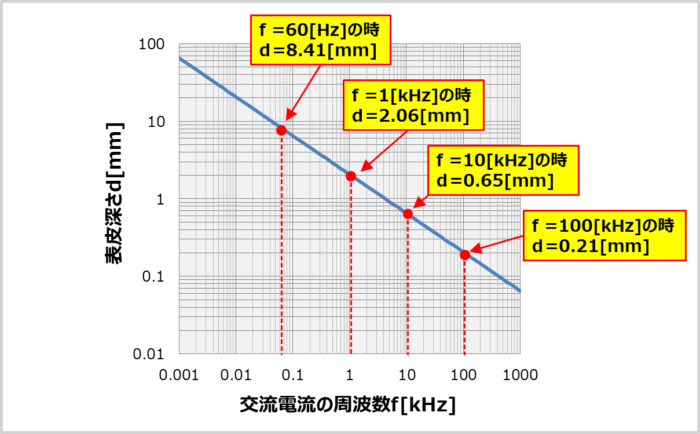

周波数\(f\)が高くなるほど、表皮深さ\(d\)が小さくなることが分かります。
表皮効果の対策
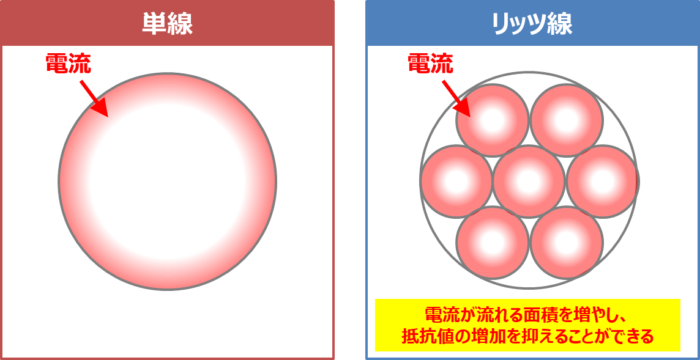

表皮効果の対策として、リッツ線(Lits Wire)を用いることがあります。
単線は1本の電線で作られている導線です。単線の場合、表皮効果により、導線の中心部に流れる電流が減少します。
そこで、絶縁された複数の細い電線がより合わさせてあるリッツ線を用いることにより、電流が流れる面積を増やし、抵抗値の増加を抑えることができます。
また、コストが上がりますが、銅の導体に銀メッキや金メッキを施して、表皮効果を低減させる対策もあります。
まとめ
この記事では『表皮効果』について、以下の内容を説明しました。
- 表皮効果とは
- 表皮効果の『原理』・『計算式』・『対策』
- 表皮深さとは
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。







