【アンペールの法則とは？】積分形と微分形の式と導出方法について！

この記事では『アンペールの法則』について

『アンペールの法則』とは
『アンペールの法則』の基本形・積分形・微分形の式と導出方法

などを図を用いて分かりやすく説明しています。

アンペールの法則とは

アンペールの法則とは、電流とその周囲にできる磁界(磁場)との関係を表す法則です。英語ではAmpère's circuital lawと書きます。アンペールの法則は1820年にフランスの物理学者アンドレ＝マリー・アンペールによって発見されました。

ではこれからこのアンペールの法則の基本形、微分形、積分形を順番に説明していきます。

磁石が磁界(磁場)を作るのはイメージが湧くと思いますが、電流も磁界(磁場)を作ることができるのです。

アンペールの法則の基本形

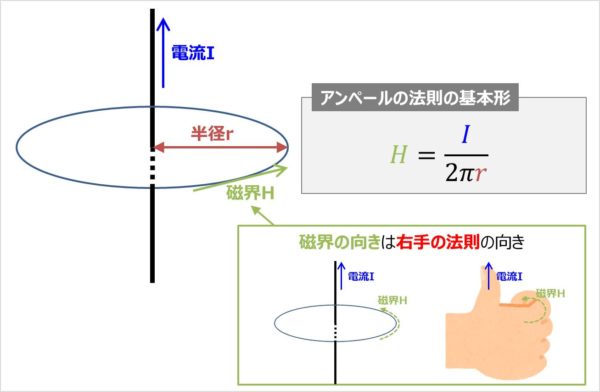
無限に長い直流導体に\(I\,\mathrm{[A]}\)の電流を流すと、直流導体の周囲には磁界(磁場)が発生します。

磁界の強さ\(H\,\mathrm{[N/Wb]}\)は直流導体から距離\(r\,\mathrm{[m]}\)離れた位置では以下の式で表すことが出来ます。

アンペールの法則の基本形

\begin{eqnarray}
H=\frac{I}{2{\pi}r}
\end{eqnarray}

上式より、磁界の強さ\(H\)は、電流\(I\)に比例し距離\(r\)に反比例することが分かります。すなわち、電流\(I\)が大きく、距離\(r\)が近いほど、磁界\(H\)は強くなるということになります。また、この磁界の強さ\(H\)は、直流導線を中心とした同心円状では等しくなるのが特徴です。

磁界の向きは右手を用いることで分かります。右手の親指を立てて手を握り、電流\(I\)の流れる方向を右手の親指にします。この時、残りの指の向きが磁界\(H\)の向きとなります。このことから、アンペールの法則は、右ねじの法則や右手の法則などと呼ばれることがあります。

補足

上式はビオ・サバールの法則を積分することで求めることができます(詳しくは専門書等をご覧ください)。

アンペールの法則の積分形

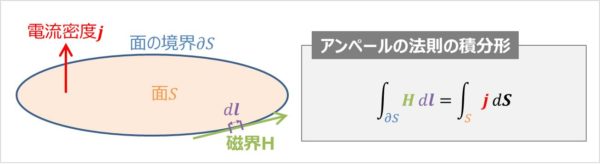
アンペールの法則の基本形では直流導体に電流\(I\,\mathrm{[A]}\)流れた時において、距離\(r\,\mathrm{[m]}\)離れた場所で発生する磁界(磁場)を考えました。

ここで、アンペールの法則の積分形では少し考え方を変えます。

磁界(磁場)側から考えると、「面の境界\({\partial}S\)において、磁界(磁場)の接線\({\boldsymbol{H}}\)を足し合わせる(積分する)と、足し合わせた結果は、面\(S\)を貫く電流\({\boldsymbol{j}}\)の和に比例する」となります。これを式で表したものがアンペールの法則の積分形であり、以下の式で表されます。

アンペールの法則の積分形

\begin{eqnarray}
\displaystyle\int_{{\partial}S}{\boldsymbol{H}}d{\boldsymbol{l}}=\displaystyle\int_{S}{\boldsymbol{j}}d{\boldsymbol{S}}
\end{eqnarray}

ここで、\(H\)は磁界の強さ、\({\boldsymbol{j}}\)は電流密度、\(d{\boldsymbol{l}}\)は線素ベクトル、\(d{\boldsymbol{S}}\)は面素ベクトル、\({{\partial}S}\)は面\(S\)の境界となります。

補足

上記のアンペールの法則の積分形を磁束密度\(B\)で表すと以下の式となります。
\begin{eqnarray}
\displaystyle\int_{{\partial}S}{\boldsymbol{B}}d{\boldsymbol{l}}={\mu}\displaystyle\int_{S}{\boldsymbol{j}}d{\boldsymbol{S}}
\end{eqnarray}

アンペールの法則の積分形から基本形に変形する方法

アンペールの積分形の左辺を変形すると、
\begin{eqnarray}
\displaystyle\int_{{\partial}S}{\boldsymbol{H}}d{\boldsymbol{l}}=H\displaystyle\int_{{\partial}S}d{\boldsymbol{l}}=2{\pi}rH
\end{eqnarray}
となります。一方右辺を変形すると、
\begin{eqnarray}
\displaystyle\int_{S}{\boldsymbol{j}}d{\boldsymbol{S}}=I
\end{eqnarray}
となります。\(I\)は面Sを貫く全電流を示しています。これらの結果から
\begin{eqnarray}
2{\pi}rH=I\\
{\Leftrightarrow}H=\frac{I}{2{\pi}r}
\end{eqnarray}
となり、最初に説明したアンペールの法則の基本形の式が導出されます。

アンペールの法則の微分形

アンペールの法則の微分形は以下の式で表されます。

アンペールの法則の微分形

\begin{eqnarray}
rot{\boldsymbol{H}}={\boldsymbol{j}}
\end{eqnarray}

上式は電流密度\({\boldsymbol{j}}\)が流れた時、その電流の周りに磁界\(rot{\boldsymbol{H}}\)が発生することを示しています。

補足

\(rot\)はrotation(ローテーション)の略であり、「回転」の意味となります。この\(rot\)は微分演算子\({\nabla}\)(ナブラ)を用いて、
\begin{eqnarray}
{\nabla}×{\boldsymbol{H}}={\boldsymbol{j}}
\end{eqnarray}
と書くこともできます。

アンペールの法則の積分形から微分形に変形する方法

アンペールの法則の積分形にストークスの定理を用いると、微分形を導出することができます。

ストークスの定理とは、「回転\(rot{\boldsymbol{A}}\)を面\(S\)で面積分したものは、接線\({\boldsymbol{A}}\)を面の境界\({{\partial}S}\)で線積分したものと等しくなる」というもので以下の式で表されます。
\begin{eqnarray}
\displaystyle\int_{S}{rot{\boldsymbol{A}}}d{\boldsymbol{S}}=\displaystyle\int_{{\partial}S}{\boldsymbol{A}}d{\boldsymbol{l}}
\end{eqnarray}

これを、アンペールの法則の積分形に当てはめてみましょう。

アンペールの法則の積分形の左辺にストークスの定理を当てはめると、
\begin{eqnarray}
\displaystyle\int_{{\partial}S}{\boldsymbol{H}}d{\boldsymbol{l}}=\displaystyle\int_{S}{rot{\boldsymbol{H}}}d{\boldsymbol{S}}
\end{eqnarray}

したがって、
\begin{eqnarray}
\displaystyle\int_{S}{rot{\boldsymbol{H}}}d{\boldsymbol{S}}=\displaystyle\int_{S}{\boldsymbol{j}}d{\boldsymbol{S}}
\end{eqnarray}

となります。ここから面積分を取ると、
\begin{eqnarray}
rot{\boldsymbol{H}}={\boldsymbol{j}}
\end{eqnarray}
となり、アンペールの法則の微分形を導出することができます。