オペアンプの『周波数特性』について！

この記事ではオペアンプの『周波数特性』について

オペアンプの『周波数特性』とは
オペアンプの『周波数特性』の関連用語(ユニティゲイン周波数と利得帯域幅積)
オペアンプに帰還回路を接続した時の『周波数特性』

などを図を用いて分かりやすく説明しています。

オペアンプの『周波数特性』

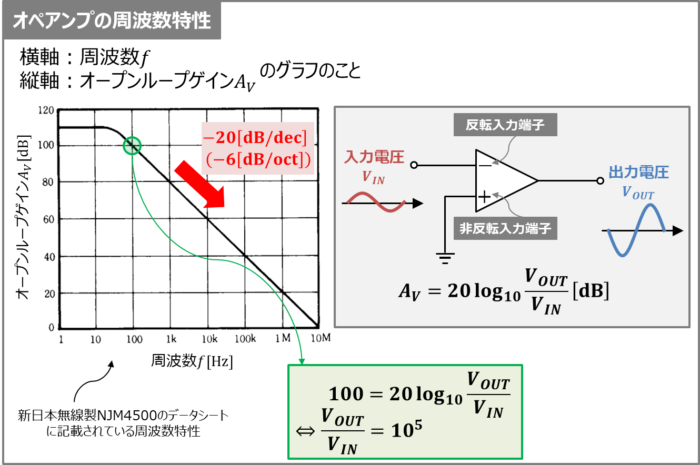
上図に示している周波数特性は新日本無線製NJM4500のデータシートに記載されている周波数特性です。

オペアンプの周波数特性とは『横軸が周波数\(f\)、縦軸がオープンループゲイン\(A_V\)』のグラフのことを指します。オープンループゲインは開ループ電圧利得、開ループ利得、開放電圧利得、開ループゲイン、オープンループ電圧利得など様々な呼び名がありますが、この記事では「オープンループゲイン」で統一します。

周波数特性は、入力電圧(振幅：\(V_{IN}\))をオペアンプの反転入力端子(オペアンプの「－」の箇所)に印加し、入力電圧の振幅を一定にしたまま、周波数\(f\)を変化させた時の出力電圧(振幅：\(V_{OUT}\))をプロットすることで取得しており、オープンループゲイン\(A_V\)は下記の式で表されます。

\begin{eqnarray}
A_V=20{\log}_{10}\frac{V_{OUT}}{V_{IN}}{\mathrm{[dB]}}\tag{1}
\end{eqnarray}

オープンループゲイン\(A_V\)の単位は\({\mathrm{[dB]}}\)(←デシベル：decibel)となっています。

『デシベル』については下記の記事で詳しく説明していますのでご参考にしてください。

: 電圧や電力の『デシベル(dB)』とは？計算方法や変換方法について
続きを見る

上図の周波数特性を見ると、周波数\(f\)が100Hzの時、オープンループゲイン\(A_V\)は100dBになっていることが分かります。この時、(1)式を用いると、入力電圧の振幅\(V_{IN}\)と出力電圧の振幅\(V_{OUT}\)の比は、以下の値となります。

\begin{eqnarray}
100&=&20{\log}_{10}\frac{V_{OUT}}{V_{IN}}\\
{\Leftrightarrow}\frac{V_{OUT}}{V_{IN}}&=&10^5\tag{2}
\end{eqnarray}

すなわち、出力電圧の振幅\(V_{OUT}\)は入力電圧の振幅\(V_{IN}\)の10万倍(10⁵倍)になるということです。入力電圧の振幅\(V_{IN}\)が0.00001Vの場合、出力電圧の振幅\(V_{OUT}\)が1Vになります。

また、理想オペアンプは無限大の周波数まで増幅できますが、実際のオペアンプでは増幅できる周波数に限界があります。上図の周波数特性を見ると、ある周波数\(f\)(10Hz過ぎ)からオープンループゲイン\(A_V\)が減少してきます。

周波数\(f\)が100Hzの時はオープンループゲイン\(A_V\)が100dB、周波数が\(f\)が1000Hz(1kHz)の時はオープンループゲイン\(A_V\)が80dBとなっており、周波数\(f\)が10倍になるとオープンループゲイン\(A_V\)が-20dBとなるため、-20[dB/dec]の傾きで減少しています。

グラフからだと分かりにくいですが、周波数\(f\)が2倍になると、オープンループゲイン\(A_V\)が-6dBになるため、-6[dB/oct]の傾きで減少しているともいいます。

周波数\(f\)が2倍になることをoct(オクターブ)、10倍になることをdec(ディケード)といいます。

次にオペアンプの周波数特性において、ユニティゲイン周波数\(f_T\)と利得帯域幅積(GB積)という関連用語があるため、これから説明します。

ユニティゲイン周波数

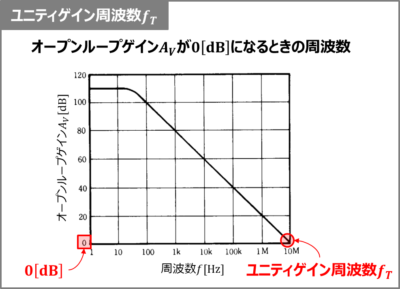
オペアンプの周波数特性において、入力電圧の周波数\(f\)を上げていくと、オープンループゲイン\(A_V\)が減少していき、やがて0[dB]となります。このゲインが0[dB]になる周波数をユニティゲイン周波数\(f_T\)といいます。ユニティゲイン周波数\(f_T\)は単一利得周波数とも呼ばれています。

入力電圧の周波数\(f\)がユニティゲイン周波数\(f_T\)以下になると、オープンループゲイン\(A_V\)が0[dB]以下となるため、増幅作用がなくなります。なぜなら、オープンループゲイン\(A_V\)が0[dB]の時、(1)式を用いると、下式に示すように\(\displaystyle\frac{V_{OUT}}{V_{IN}}\)が1となるからです。

\begin{eqnarray}
0&=&20{\log}_{10}\displaystyle\frac{V_{OUT}}{V_{IN}}\\
{\Leftrightarrow}\displaystyle\frac{V_{OUT}}{V_{IN}}&=&1\tag{3}
\end{eqnarray}

また、オープンループゲイン\(A_V\)が0[dB]以下の時、\(\displaystyle\frac{V_{OUT}}{V_{IN}}{≤}1\)となるため、出力電圧の振幅\(V_{OUT}\)は入力電圧の振幅\(V_{IN}\)より小さくなります。

ユニティゲイン周波数\(f_T\)が高いほど、オープンループゲイン\(A_V\)が0[dB]となる周波数が高いということなので、高周波まで増幅作用があるオペアンプとなります。

利得帯域幅積(GB積)

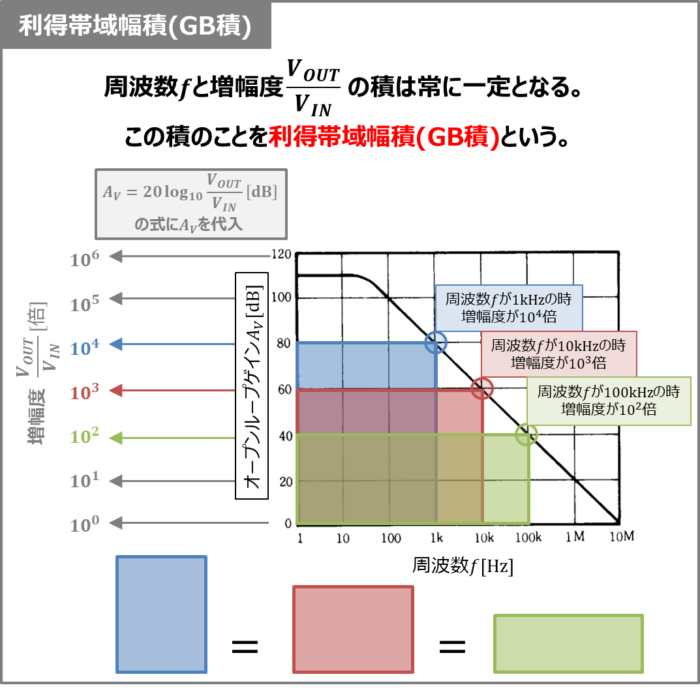
オペアンプの周波数特性において、入力電圧の周波数\(f\)が100Hzの時の増幅度\(\displaystyle\frac{V_{OUT}}{V_{IN}}\)は10⁵倍となっており、入力電圧の周波数\(f\)を上げていくと下記のように変化します。

入力電圧の周波数\(f\)が1kHzの時

増幅度\(\displaystyle\frac{V_{OUT}}{V_{IN}}\)は10⁴倍

入力電圧の周波数\(f\)が10kHzの時

増幅度\(\displaystyle\frac{V_{OUT}}{V_{IN}}\)は10³倍

入力電圧の周波数\(f\)が100kHzの時

増幅度\(\displaystyle\frac{V_{OUT}}{V_{IN}}\)は10²倍

このように、入力電圧の周波数\(f\)が10倍になると増幅度\(\displaystyle\frac{V_{OUT}}{V_{IN}}\)が1/10倍となっており、周波数\(f\)と増幅度\(\displaystyle\frac{V_{OUT}}{V_{IN}}\)の積は常に一定となります。この積のことを利得帯域幅積といいます。利得帯域幅積はGB積やゲインバンド積とも呼ばれています。

オペアンプに帰還回路を接続した場合の『周波数特性』

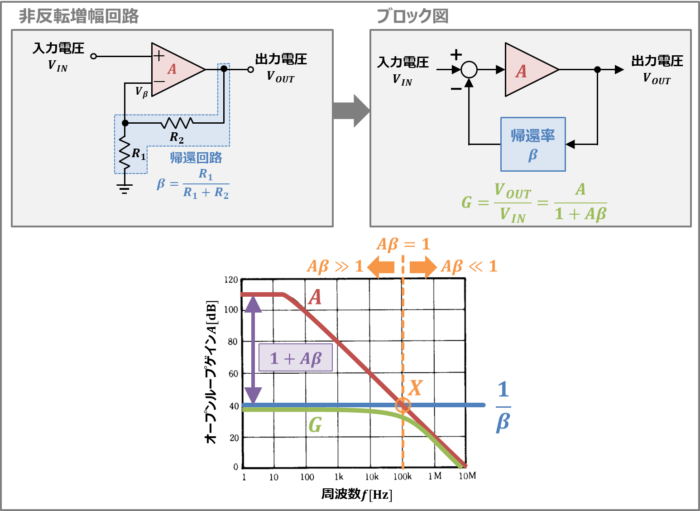
オペアンプを実際に使用する時には帰還回路によりフィードバックをかけて使用します。

ここからは帰還回路を用いた時の周波数特性について、一例として非反転増幅回路を取り上げて説明します。

非反転増幅回路は抵抗\(R_1\)と抵抗\(R_2\)で帰還回路を形成している回路です。出力電圧を抵抗\(R_1\)と抵抗\(R_2\)で分圧したものをオペアンプの反転入力端子(オペアンプの「－」の箇所)に入力しています。

『非反転増幅回路』については下記の記事で詳しく説明していますのでご参考にしてください。

あわせて読みたい

: 『非反転増幅回路』を分かりやすく解説！【オペアンプ】
続きを見る

また、上図の右上にオペアンプ(オープンループゲイン\(A\))と帰還回路(帰還率：\(β\)、ゲイン：\(\displaystyle\frac{1}{β}\))から構成されるオペアンプ回路のブロック図を示しています。フィードバックを掛けたときのゲインをクローズドループゲイン(閉ループ電圧利得)といいます。クローズドループゲイン\(G\)は次式で表されます。

\begin{eqnarray}
G=\frac{V_{OUT}}{V_{IN}}=\frac{A}{1+Aβ}\tag{4}
\end{eqnarray}

(4)式において、クローズドループゲイン\(G\)は\(Aβ\)(ループゲインやループ利得と呼ばれる)の大小に応じて以下のように近似することができます。

\begin{eqnarray}
Aβ{\;}{\gg}{\;}1の時&：&\frac{V_{OUT}}{V_{IN}}{\;}{\approx}{\;}\frac{1}{β}\\
Aβ{\;}{\ll}{\;}1の時&：&\frac{V_{OUT}}{V_{IN}}{\;}{\approx}{\;}A
\end{eqnarray}

すなわち、クローズドループゲイン\(G\)には以下の特徴があるということになります。

クローズドループゲインGの特徴

ループゲイン\(Aβ\)が大きい周波数範囲(\(Aβ{\;}{\gg}{\;}1\)の時)

クローズドループゲイン\(G\)は帰還回路のゲイン\(\displaystyle\frac{1}{β}\)が支配的になる。

ループゲイン\(Aβ\)が小さい周波数範囲(\(Aβ{\;}{\ll}{\;}1\)の時)

クローズドループゲイン\(G\)はオペアンプ単体のオープンループゲイン\(A\)が支配的になる。

また、帰還回路の帰還率\(β\)とゲイン\(\displaystyle\frac{1}{β}\)は抵抗\(R_1\)と抵抗\(R_2\)による分圧回路であり下記の値となります。

\begin{eqnarray}
β&=&\frac{R_1}{R_1+R_2}\\
\displaystyle\frac{1}{β}&=&1+\frac{R_2}{R_1}
\end{eqnarray}

帰還回路のゲイン\(\displaystyle\frac{1}{β}\)をdBに変換したものをオペアンプの周波数特性に引きます(青線)。オペアンプ単体のオープンループゲイン\(A\)と帰還回路のゲイン\(\displaystyle\frac{1}{β}\)の交点Xが周波数の上限値であり、交点Xより周波数が高くなると、クローズドループゲイン\(G\)が大きく減少します。また、帰還回路のゲイン\(\displaystyle\frac{1}{β}\)が高くなるほど、オペアンプ単体のオープンループゲイン\(A\)との交点Xが低周波になるため、周波数帯域が狭くなります。

また、上図において、交点Xではオペアンプ単体のオープンループゲイン\(A\)と帰還回路のゲイン\(\displaystyle\frac{1}{β}\)が等しくなるため、\(Aβ=1\)となります。交点Xより左側では\(A\)が\(\displaystyle\frac{1}{β}\)より大きいため\(Aβ{\;}{\gg}{\;}1\)、交点Xより右側では\(A\)が\(\displaystyle\frac{1}{β}\)より小さいため、\(Aβ{\;}{\ll}{\;}1\)となります。

すなわち、オペアンプに帰還回路を接続した場合の『周波数特性』は下記のように変化します。

オペアンプに帰還回路を接続した場合の『周波数特性』

交点X(\(Aβ=1\))より左側(\(Aβ{\;}{\gg}{\;}1\)の時)

クローズドループゲイン\(G\)は帰還回路のゲイン\(\displaystyle\frac{1}{β}\)が支配的になる。

交点X(\(Aβ=1\))より右側(\(Aβ{\;}{\ll}{\;}1\)の時)

クローズドループゲイン\(G\)はオペアンプ単体のオープンループゲイン\(A\)が支配的になる。

したがって、クローズドループゲイン\(G\)の『周波数特性』は緑線のようになります。このように、クローズドループゲイン\(G\)は主に帰還回路のゲイン\(\displaystyle\frac{1}{β}\)により決まっており、周波数の上限値はオペアンプ単体のオープンループゲイン\(A\)と帰還回路のゲイン\(\displaystyle\frac{1}{β}\)の交点Xで決まります。

非反転増幅回路の入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の関係は以下の式で表されているのが一般的ですが、これはオペアンプ単体のオープンループゲイン\(A\)を無限大とした時の概算値であることに注意してください。

\begin{eqnarray}
\frac{V_{OUT}}{V_{IN}}=1+\frac{R_2}{R_1}
\end{eqnarray}

その他の関連用語