ダイオードの『繰り返しせん頭サージ逆電力PRRSM』について！

この記事ではダイオードの絶対最大定格に記載されていることがある『繰り返しせん頭サージ逆電力\(P_{RRSM}\)』について説明しています。

ダイオードの『繰り返しせん頭サージ逆電力P_RRSM』

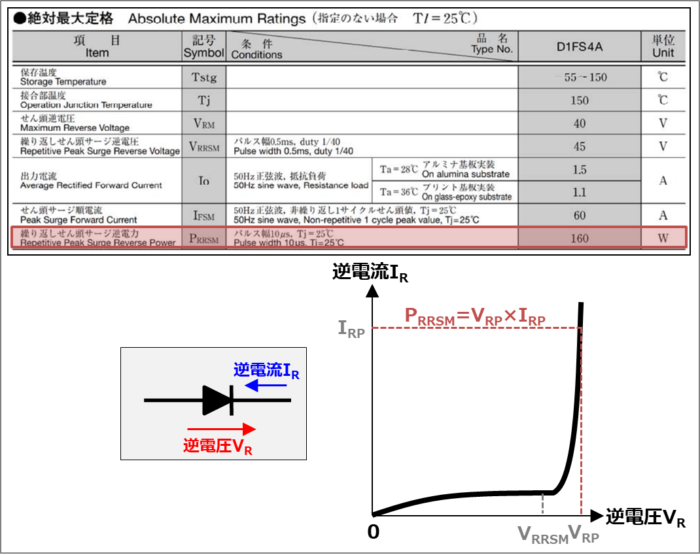
データシートの絶対最大定格に記載されていることがある『繰り返しせん頭サージ逆電力\(P_{RRSM}\)』は指定条件にて繰り返しで印加できる逆方向電力のピーク値です。

繰り返しせん頭サージ逆電力\(P_{RRSM}\)は『逆方向電圧のピーク値\(V_{RP}\)』と『その時に流れる漏れ電流のピーク値\(I_{RP}\)』の積であり、次式で表されます。

\begin{eqnarray}
P_{RRSM}=V_{RP}×I_{RP}\tag{1}
\end{eqnarray}

ダイオードに印加される逆電圧が『繰り返しせん頭サージ逆電圧\(V_{RRSM}\)』を超える場合には、『繰り返しせん頭サージ逆電力\(P_{RRSM}\)』が適用できるかを検討します。

『繰り返しせん頭サージ逆電圧\(V_{RRSM}\)』については下記の記事で詳しく説明していますのでご参考にしてください。

ダイオードの『繰り返しせん頭サージ逆電力P_RRSM』の値と使い方

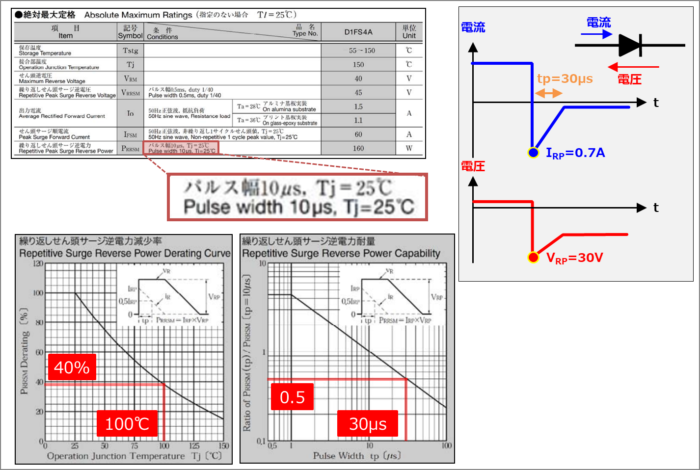
上図に示しているのは、新電元工業製ダイオードD1FS4Aの『絶対最大定格』、『繰り返しせん頭サージ逆電力減少率』、『繰り返しせん頭サージ逆電力耐量』です。絶対最大定格を見ると、指定条件は「\(T_{j}=25{\mathrm{℃}}\)、\(t_{p}=10{\mathrm{μs}}\)」であると分かります。

ダイオードD1FS4Aに流れている電流と印加されている電圧が上図の右のような波形の時における繰り返しせん頭サージ逆電力\(P_{RRSM}(実波形)\)を求めてみます(接合温度は\(T_{j}=100{\mathrm{℃}}\)とします)。繰り返しせん頭サージ逆電力\(P_{RRSM}\)を接合温度\(T_{j}\)でディレーティングを行い、パルス幅\(t_{p}\)で換算した値が実波形の\(P_{RRSM}(実波形)\)よりも大きければ使用可能となります。

実波形の繰り返しせん頭サージ逆電力\(P_{RRSM}(実波形)\)は次式となります。

\begin{eqnarray}
P_{RRSM}(実波形)=V_{RP}×I_{RP}=30{\mathrm{[V]}}×0.7{\mathrm{[A]}}=21{\mathrm{[W]}}\tag{2}
\end{eqnarray}

また、『絶対最大定格』の表より、繰り返しせん頭サージ逆電力\(P_{RRSM}\)の定格(\(T_{j}=25℃\)、\(t_{p}=10{\mathrm{μs}}\))は\(160{\mathrm{W}}\)となります。

\begin{eqnarray}
P_{RRSM}(T_{j}=25℃,t_{p}=10μs)=160{\mathrm{[W]}}\tag{3}
\end{eqnarray}

接合温度\(T_{j}\)は\(100{\mathrm{℃}}\)なので、『繰り返しせん頭サージ逆電力減少率』を用いてディレーティングします。『繰り返しせん頭サージ逆電力減少率』は横軸が接合温度\(T_{j}\)で、縦軸が電力ディレーティングの特性です。接合温度\(T_{j}\)が高くなるほど電力ディレーティングが減少します。\(T_{j}=100{\mathrm{℃}}\)では電力ディレーティングは約40%となるため、繰り返しせん頭サージ逆電力\(P_{RRSM}\)の定格(\(T_{j}=100{\mathrm{℃}}\)、\(t_{p}=10{\mathrm{μs}}\))は以下の値となります。

\begin{eqnarray}
P_{RRSM}(T_{j}=100℃,t_{p}=10μs)&=&P_{RRSM}(T_{j}=25℃,t_{p}=10μs)×0.4\\
&=&160{\mathrm{[W]}}×0.4\\
&=&56{\mathrm{[W]}}\tag{4}
\end{eqnarray}

また、パルス幅\(t_{p}\)は\(30{\mathrm{μs}}\)なので、『繰り返しせん頭サージ逆電力耐量』を用いて換算します。『繰り返しせん頭サージ逆電力耐量』は横軸がパルス幅\(t_{p}\)で、縦軸が『割合\(\displaystyle\frac{P_{RRSM}(t_{p})}{P_{RRSM}(10{\mathrm{μs}})}\)』の特性です。パルス幅\(t_{p}\)が長くなるほど割合が小さくなります。\(t_{p}=30{\mathrm{μs}}\)における繰り返しせん頭サージ逆電力\(P_{RRSM}\)の定格(\(T_{j}=100{\mathrm{℃}}\),\(t_{p}=30{\mathrm{μs}}\)は以下の値となります。

\begin{eqnarray}
P_{RRSM}(T_{j}=100℃,t_{p}=30μs)&=&P_{RRSM}(T_{j}=100℃,t_{p}=10μs)×\frac{P_{RRSM}(30μs)}{P_{RRSM}(10μs)}\\
&=&56{\mathrm{[W]}}×0.5\\
&=&28{\mathrm{[W]}}\tag{5}
\end{eqnarray}

上値より、\(P_{RRSM}(T_{j}=100℃、t_{p}=30μs)\)は\(P_{RRSM}(実波形)\)よりも大きいため、使用可能と判断できます。

補足

繰り返しせん頭サージ逆電力は英語では『Repetitive Peak Surge Reverse Power』と書きます。
ダイオードの電力定格には、せん頭サージ電力\(P_{SM}\)というものがあります。\(P_{SM}\)は規定されたインパルス波形で印加し得る最大の最大ピーク電力値となっています。